手撕代码:初始化、正则化和梯度检验
首先先给出绘制决策边界的函数:
def plot_decison_boundary(model,X,y):
x_min,x_max = X[0,:].min()-1 , X[0,:].max()+1
y_min,y_max = X[1,:].min()-1 , X[1,:].max()+1
h = 0.01
#meshgrid(a,b)将a纵向排列,将b横向排列,组合坐标;再将这些坐标的x值组成的多维数组返回 给xx,y值组成的多维数组返回给yy
xx,yy = np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
#ravel()将多维数组压缩成一维,c_()将多个数组沿axis=1拼接
Z = model(np.c_[xx.ravel(),yy.ravel()])
Z = Z.reshape(xx.shape)
#Z的维度和xx/yy一致,contourf()用于绘制并填充等高线图,xx给出了绘制点的横坐标,yy给出 了绘制点的纵坐标,Z给出了对应绘制点的高度
plt.contourf(xx,yy,Z,cmap=plt.cm.Spectral)
plt.xlabel("x1")
plt.ylabel("x2")
#绘制散点图
plt.scatter(X[0,:],X[1,:],c=np.squeeze(y),cmap=plt.cm.Spectral)
plt.show()
一、不同初始化方法对结果的影响
- 全零初始化:
#初始化为零
def initialization_param_zeros(layers_dims):
param = {}
L = len(layers_dims)
for i in range(1,L):
param["W"+str(i)] = np.zeros((layers_dims[i],layers_dims[i-1]))
param["b"+str(i)] = np.zeros((layers_dims[i],1))
return param
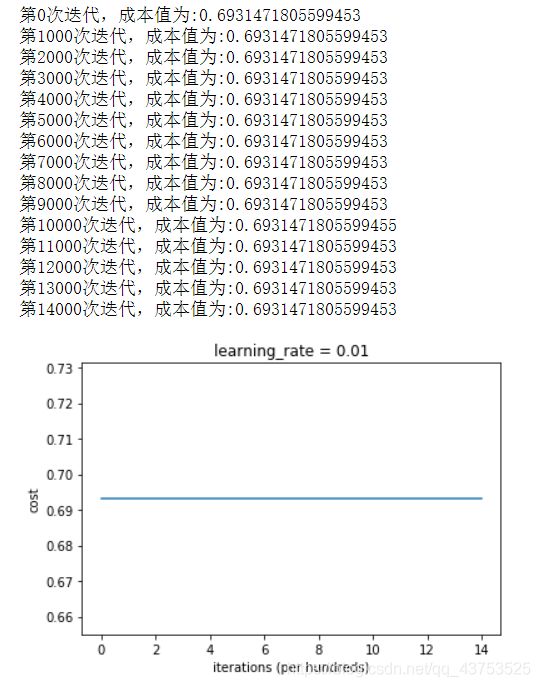
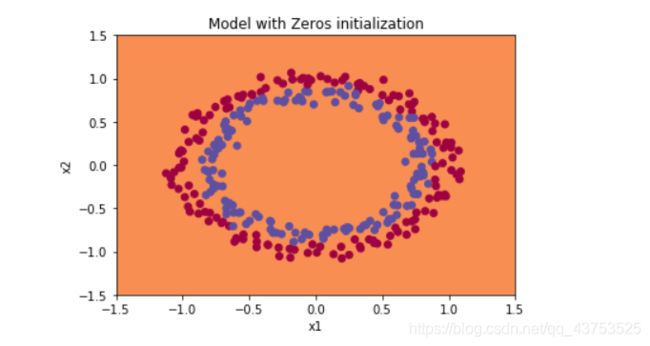
全零初始化导致神经网络无法打破对称性,没有学习能力,如下图所示:
决策边界如下图所示:
- 随机初始化:
#随机初始化
def initialization_param_random(layers_dims):
np.random.seed(3)
param = {}
L = len(layers_dims)
for i in range(1,L):
#随机形成的参数矩阵的系数是与第三种初始化方法的区别
param["W"+str(i)] = np.random.randn(layers_dims[i],layers_dims[i-1]) * 10
param["b"+str(i)] = np.zeros((layers_dims[i],1))
return param
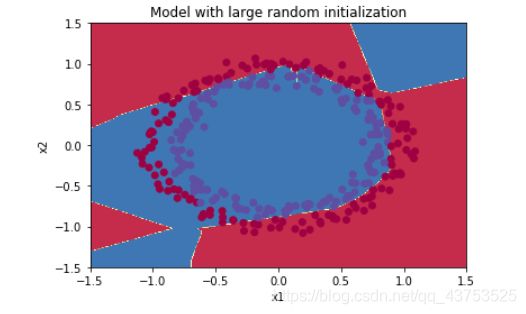
随机初始化有一定的学习能力,但学习速度不如第三种初始化方法快,效果如下图所示:
- 抑梯度异常初始化
#抑梯度异常初始化
def initialization_param_random(layers_dims):
np.random.seed(3)
param = {}
L = len(layers_dims)
for i in range(1,L):
#留意随机初始化参数矩阵的系数,不同激活函数适用的系数不同
param["W"+str(i)] = np.random.randn(layers_dims[i],layers_dims[i-1]) * np.sqrt(2/layers_dims[i-1])
param["b"+str(i)] = np.zeros((layers_dims[i],1))
return param
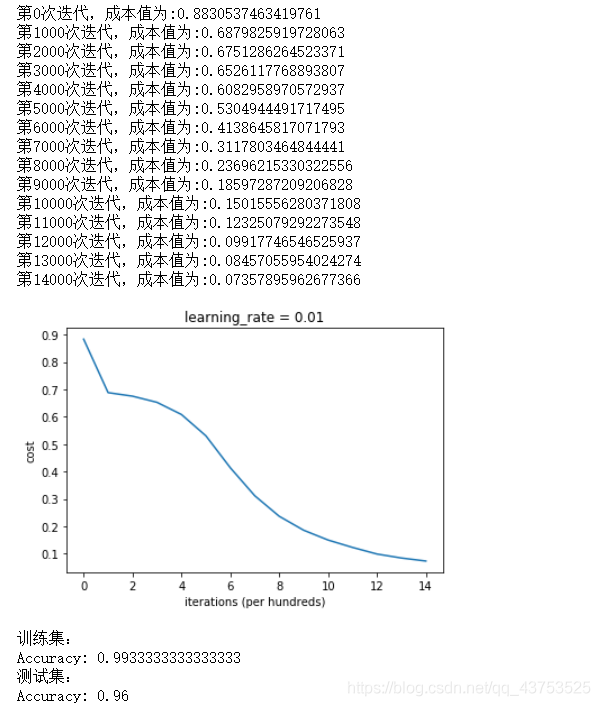
学习效果如下图所示,可见效果和学习速度均比随机初始化好:
二、不同正则化方法对结果的影响
若L2正则化和dropout正则化不同时使用,则模型代码实现如下。L2正则化只需修改:一计算成本,二反向传播;dropout正则化只需修改:一正向传播,二反向传播
def model(X,Y,learning_rate=0.3,num_iterations=30000,print_cost=True,is_plot=True,
lambd=0,keep_prob=1):
costs = []
grads = {}
layers_dims = [X.shape[0],20,3,1]
param = reg_utils.initialize_parameters(layers_dims)
for i in range(num_iterations):
#前向传播
if keep_prob == 1:
a3,cache = reg_utils.forward_propagation(X,param)
else:
a3,cache = forward_propagation_with_dropout(X,param,keep_prob)
#计算成本
if lambd == 0:
cost = reg_utils.compute_cost(a3,Y)
else:
cost = compute_cost_with_regularization(a3,Y,param,lambd)
#反向传播
#不适用正则化和dropout
if lambd==0 and keep_prob==1:
grads = reg_utils.backward_propagation(X,Y,cache)
#使用正则化,不适用dropout
elif lambd!=0 and keep_prob==1:
grads = backward_propagation_with_regularization(X,Y,cache,lambd)
#不使用正则化,使用dropout
elif lambd==0 and keep_prob!=1:
grads = backward_propagation_with_dropout(X,Y,cache,keep_prob)
#更新参数
param = reg_utils.update_parameters(param,grads,learning_rate)
#打印成本
if i%10000 == 0:
costs.append(cost)
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return param
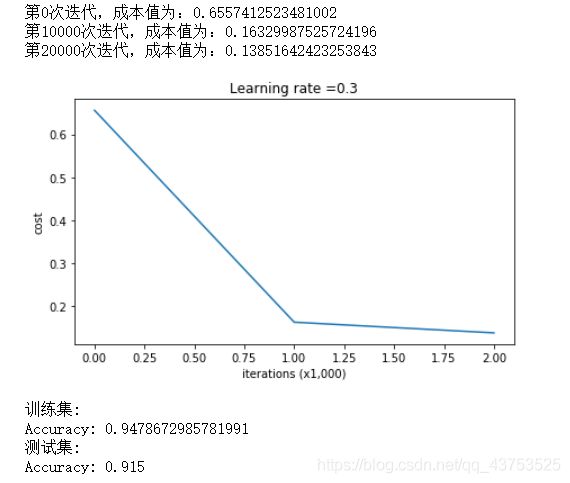
- 若不使用任何正则化方法,学习效果和决策边界如下所示:可以看到模型在测试集上的效果不如训练集,决策边界曲线复杂,存在过拟合现象
- L2正则化:
实现L2正则化需要修改:一成本函数;二反向传播
def compute_cost_with_regularization(A3,Y,param,lambd):
m = Y.shape[1]
W1 = param["W1"]
W2 = param["W2"]
W3 = param["W3"]
cross_entropy_cost = reg_utils.compute_cost(A3,Y)
#修改部分
L2_regularization_cost = (lambd/(2*m)) * (np.sum(np.square(W1))
+ np.sum(np.square(W2)) + np.sum(np.square(W3)))
cost = cross_entropy_cost + L2_regularization_cost
return cost
def backward_propagation_with_regularization(X,Y,cache,lambd):
m = Y.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
#修改部分
dW3 = (1/m) * np.dot(dZ3,A2.T) + ((lambd * W3)/m)
db3 = (1 / m) * np.sum(dZ3,axis=1,keepdims=True)
dA2 = np.dot(W3.T,dZ3)
dZ2 = dA2 * np.int64(A2>0)
#修改部分
dW2 = (1 / m) * np.dot(dZ2,A1.T) + ((lambd * W2) / m)
db2 = (1 / m) * np.sum(dZ2,axis=1,keepdims=True)
dA1 = np.dot(W2.T,dZ2)
dZ1 = dA1 * np.int64(A1>0)
#修改部分
dW1 = (1 / m) * np.dot(dZ1,X.T) + ((lambd * W1) / m)
db1 = (1 / m) * np.sum(dZ1,axis=1,keepdims=True)
grads = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return grads
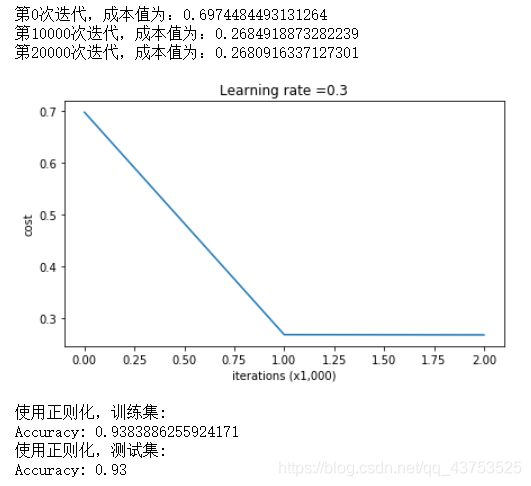
学习效果和决策曲线如下所示,过拟合现象缓解:
- dropout正则化:
实现dropout正则化需要修改:一正向传播的A;二反向传播dA
def forward_propagation_with_dropout(X,param,keep_prob=0.5):
np.random.seed(1)
W1 = param["W1"]
b1 = param["b1"]
W2 = param["W2"]
b2 = param["b2"]
W3 = param["W3"]
b3 = param["b3"]
Z1 = np.dot(W1,X) + b1
A1 = reg_utils.relu(Z1)
D1 = np.random.rand(A1.shape[0],A1.shape[1])
D1 = D1 < keep_prob
A1 = A1 * D1
A1 = A1 / keep_prob
Z2 = np.dot(W2,A1) + b2
A2 = reg_utils.relu(Z2)
D2 = np.random.rand(A2.shape[0],A2.shape[1])
D2 = D2 < keep_prob
A2 = A2 * D2
A2 = A2 / keep_prob
Z3 = np.dot(W3,A2) + b3
A3 = reg_utils.sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3,cache
def backward_propagation_with_dropout(X,Y,cache,keep_prob):
m = Y.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1/m) * np.dot(dZ3,A2.T)
db3 = (1/m) * np.sum(dZ3,axis=1,keepdims=True)
dA2 = np.dot(W3.T,dZ3)
dA2 = dA2 * D2
dA2 = dA2 / keep_prob
dZ2 = dA2 * np.int64(A2>0)
dW2 = (1/m) * np.dot(dZ2,A1.T)
db2 = (1/m) * np.sum(dZ2,axis=1,keepdims=True)
dA1 = np.dot(W2.T,dZ2)
dA1 = dA1 * D1
dA1 = dA1 / keep_prob
dZ1 = dA1 * np.int64(A1>0)
dW1 = (1/m) * np.dot(dZ1,X.T)
db1 = (1/m) * np.sum(dZ1,axis=1,keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
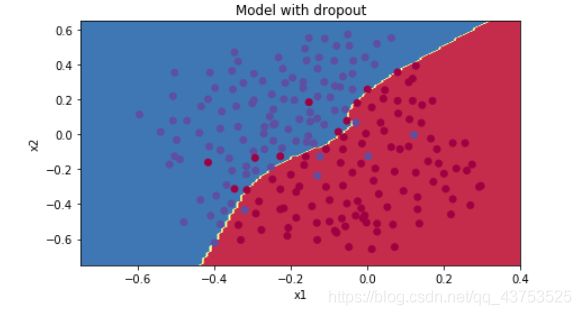
学习效果和决策边界如下:
三、梯度检验
梯度检验发生在每一次完整实现前向、反向传播之后,其实现步骤为:
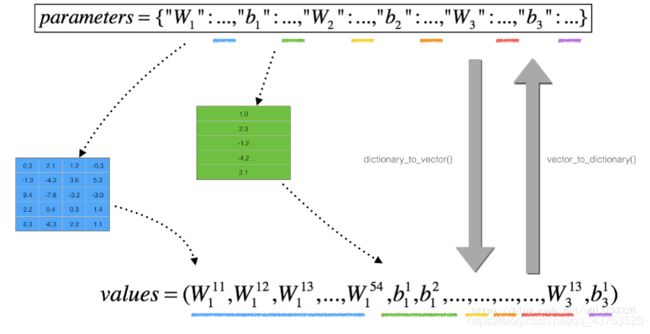
- 将params矩阵,grads矩阵reshape成一个一维数组
- 遍历params数组,每次只改变一个参数(向量化实现不了),利用双边误差公式计算出梯度的近似值
代码实现如下:
def gradient_check_n(parameters,gradients,X,Y,epsilon=1e-7):
#初始化参数
parameters_values , keys = gc_utils.dictionary_to_vector(parameters) #keys用不到
grad = gc_utils.gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters,1))
J_minus = np.zeros((num_parameters,1))
gradapprox = np.zeros((num_parameters,1))
#计算gradapprox
for i in range(num_parameters):
#计算J_plus [i]。输入:“parameters_values,epsilon”。输出=“J_plus [i]”
thetaplus = np.copy(parameters_values) # Step 1
thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaplus)) # Step 3 ,cache用不到
#计算J_minus [i]。输入:“parameters_values,epsilon”。输出=“J_minus [i]”。
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i][0] = thetaminus[i][0] - epsilon # Step 2
J_minus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaminus))# Step 3 ,cache用不到
#计算gradapprox[i]
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
#通过计算差异比较gradapprox和后向传播梯度。
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
if difference < 1e-7:
print("梯度检查:梯度正常!")
else:
print("梯度检查:梯度超出阈值!")
return difference