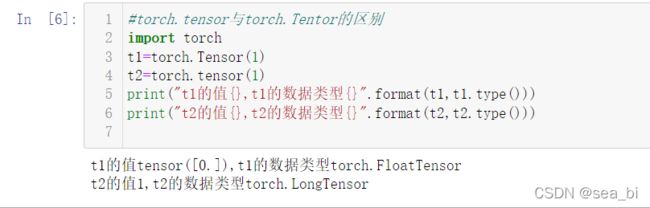
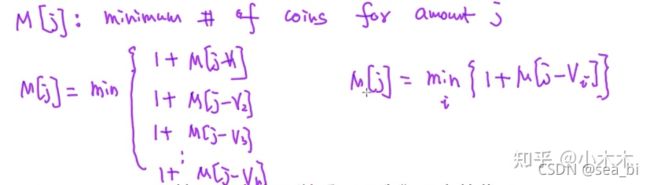贪心自然语言处理学习笔记

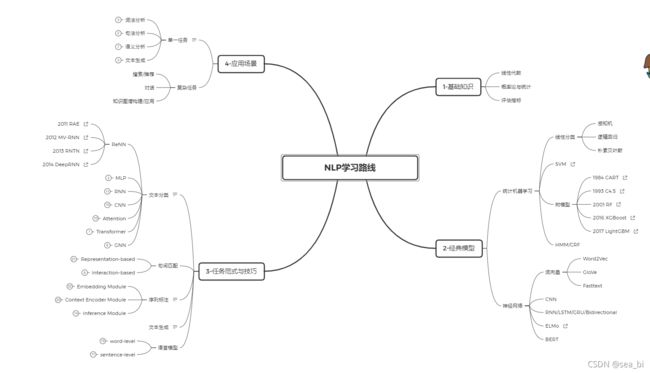
NLP学习路线

开始记录学习nlp，学习路线参考博主的建议，后续把这部分的内容进行整理。

---

前言

要学好NLP，下面3个是缺一不可的： 1. 机器学习基础 人工智能很多技术和模块是搭建在机器学习基础上的，无论是CV，NLP，语音识别。可以直接去学习一个方向，也能学到东西。 但是可能不能很好的理解技术和模型背后的细节。 2. 数据结构与算法 在工程上写一个算法，如果不懂数据结构和算法，写出来的程序可能效率不高，达不到上线的要求。所以要懂数据结构和算法，才能写出最优化，性能高的程序。 3. 良好的编程基础 有良好的编程基础才能写出好的程序，不只是会讲讲理论，还能够实现出来，达到落地的地步。 在有了上面的基础后，学完自然语言的基础知识。然后需要在NLP里选择一个技术路线或者应用领域。比如预训练模型BERT，图神经网络。或者选择一个领域，智能对话系统，自然语言生成等，在某一个领域深入下去，把领域内的方方面面知识点都搞明白能够串起来。我们要使自己成为一个T字型的人才，有一个的知识的宽度，同时一定要在某方面有深度。 同时我们要养成读论文的习惯，比如在工作中突然来了一个新的需求，这时候就需要去读读论文，看看别人的思路，做一个baseline出来，然后再此基础上进行改进。

---

1、自然语言处理

自然语言处理 = Natural Language Processing = NLP

自然语言理解 = Natural Language Understanding = NLU = 理解文本中的意思

自然语言生成 = Natural Language Generation = NLG = 根据意思生成文本

例1） 一个人在看百度贴吧看帖子的时候， 首先是看帖子，这是一个理解文本内容(NLU)的过程， 然后回答帖子，这是一个生成文本(NLG)的过程。

例2） 人类在语言交流的时候

1） 听到对方的声音讯号， 根据从小学习的语文， 转换成一串文字。 （语音识别）

2） 对这段文字进行理解。 （NLU）

3） 回复对方。 （NLG)

1.1 为什么自然语言处理难?

图片：所见即所得。
文字：看到的是文字，要理解背后的含义。

1） CV的图像，一眼看过去，图片内容很直观明了。比如图片中一只狗在追一只猫，看图片就知道内容，很少有要揣摩图片意思的应用场景， 基本都是图片分类，目标检测等。
2） 自然语言的理解，想想我们从小学习的古诗还有阅读理解，要进行前后文内容的结合，才能回答问题； 还有一词多义， 一句多义等。 还有一个场景，有人突然说了一句话，听的多个人听完后可能理解的意思是不一样的。

1.2 自然语言处理技术的三个维度

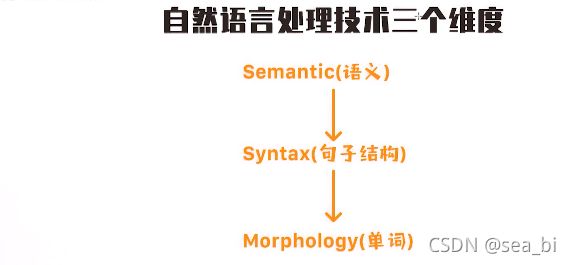
自然语言理解是从上到下的一个过程：单词->句子结构->句子含义

Morphology（单词） ：构成语言的最小单位，单词本身含义，词性

Syntax（句子结构）：句子剖析，主语+谓语+宾语，语法树

Semantic（语义）：这句话的含义， 最终的目的地

1.3 NLP基础任务

nlp基础任务主要分为以下几点：

1、分词(Word Segmentation):单词是句子最小的单位，要把句子切分完后做特征工程，中文比英文要难些，英文天生空格或其他符号就能切分，中文要借助一些算法才能分出一个比较好的结果。分词是NLP任务的第一步，是已经解决的问题。
2. 词性分析(Part-of-Speech Tagging):对后续单词理解是有帮助的，词性也可以作为后续任务的特征。非常基础的工作，是已经解决的比较好的问题。
3. 语义理解(Semantic Understanding):理解一句话的含义，NLP领域的核心。例如Bert本身也是为了很好的理解一个单词，以达到更好的理解一句话。
4. 命名实体识别(Named Entity Recognition)：比较基础的任务，现实生活中实际存在的一个物体，比如人，地名，公司名，组织名，时间。 医疗领域：科室，药名。 实体是在一个领域里比较有含义的单词，通常是给一个文本，任务是把实体标记出来。 像聊天机器人，意图识别，知识图谱等场景中，命名实体识别对后续的任务有非常大的帮助。
5. 依存文法分析(Dependecy Parsing):语法分析领域的重要技术，单词之间的依存关系。
6. 句法分析(Parsing)：对一句话的结构，主谓宾来进行剖析，语法树。实际应用场景比较少，即使有也对系统提升比较小。 依存文法分析通常价值比句法分析大。
7. 自然语言处理技术概览

1.4 算法复杂度

对于复杂度的理解是至关重要的。写完任何一个程序，我们都需要仔细思考程序的效率如何。这个效率可以从两个方面来考虑，一方面是时间复杂度，另外一方面是空间复杂度。
算法复杂度衡量的是一个算法的效率，比如一个算法运行下来需要多长时间?需要消耗多少资源？根据算法复杂度，我们可以评估一个算法的优劣。在算法复杂度的衡量上，我们经常使用Big O表示法
复杂度的理解是必修课。在从事AI工作中经常会碰到各种各样程序效率低的问题，一个模型训练起来可能需要几天甚至几个月。这时候最直接的解决方式就是加机器，但也是最笨的方法。作为一名AI工程师，我们首先需要想到如何从根本上优化算法，比如检查是否使用了合理的数据结构? 如果一个程序需要经常做数据的查询，那这时候你要考虑用像哈希等合理的数据结构了。相反，如果你用的是列表(list)，查询速度就会变得很慢。
再比如，假设我们需要寻找一堆数据中的最大的几个数，很多人可能会选择先把所有的数做排序，之后在提取最大的前几个。但有没有比这个更高效的做法呢? 实际上，在这个场景，我们可以使用一个优先队列(priority queue)来更快速地做查询。 所以，你可以看到每一个小的细节决定了整个程序的效率。这也是为什么一定要重视算法复杂度的原因。
算法复杂度不是衡量程序跑了几秒，而是分析算法效率的级别，线性与问题的大小，平方与问题大小，三次方与问题大小。
复杂度从下面两个角度去衡量1）时间复杂度：用了多少时间； 2）空间复杂度：用了多少内存空间

1） 时间复杂度

随着n的增加，时间增长的趋势

// O(1)的时间复杂度
int x = 0;
int y = 1;

// O(n)时间复杂度
for (int i = 1; i < =n;i++）{
       x++；
}

// O(n^2)时间复杂度
for (int i = 1; i < =n;i++）{
   for (int j= 1; j< =n;j++）{
       x++；
   }
}

//
// O(n+n^2) = O(n^2)时间复杂度
for (int i = 1; i < =n;i++）{
       x++；
}

for (int i = 1; i < =n;i++）{
   for (int j= 1; j< =n;j++）{
       x++；
   }
}

//O(LogN)的算法复杂度
int i = 1;
while (i<n)
    i = i * 2;

//O(NLogN)的算法复杂度
for (int i = 1; i < =n;i++）{
  int i = 1;
  while (i<n)
     i = i * 2;
}

2. 空间复杂度

随着n的增加，空间增长的趋势

// O(1)的空间复杂度
int x = 0;
int y = 1;
 
// O(n)的空间复杂度
int[] nums = new int[n];
for(int i = 0; i< n;i++){
   nums[i]=i;
}

//O(n^2)的空间复杂度
matrix，矩阵分配空间,下面为一个n*n的方阵的内存分配
void malloc2D_1(int **&a, int n)
{
    a = new int*[n];
    for(int i=0;i<n;i++)     
        a[i] = new int[n];
}

3） 斐波那契数列的时间复杂度

O（2^n) :计算加法所执行的次数

F[n]=F[n-1]+Fn-2

实现：

def fb(n):
    if n==0:
        return 0
    if n==1:
        return 1
    return fb(n-1)+fb(n-2)



if __name__ == "__main__":
    s=fb(9)
    print(s)

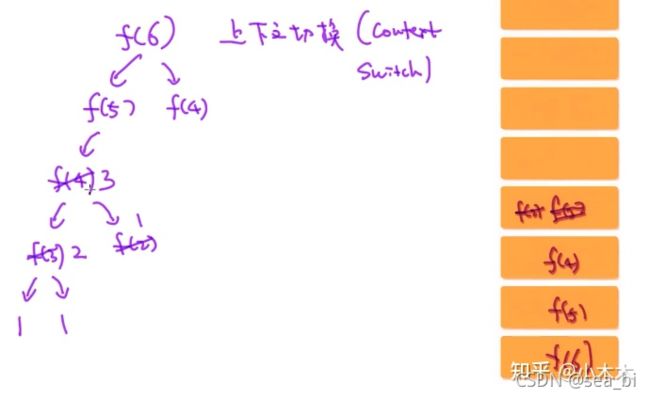
4） 斐波那契数列的空间复杂度

O（n) : 计算时最多入栈的数据的数量，递归调用函数时，会进行上下文切换，对当前函数中的状态进行入栈操作，当调用函数返回时，进行出栈操作。

1.5 动态规划算法

动态规划的核心思想：把计算结果存入内存， 需要的时候从内存里取出来。
为了解决一个大的问题，我们从小问题开始解决。 但一旦解决了小问题，我们就把这些问题的答案存放在内存空间为后续提供使用。所以对于动态规划算法有几个关键点:
1、子问题：思考如何把一个问题拆解成更小的子问题? 并把大问题以子问题的形式表示出来?
2、结果存放：如何存放过程结果?
实际例子：最大递增子串

import numpy as np
import sys
def max_subseq_sum(arr):
  max_so_far = -sys.maxsize     #取系统的最大值
  max_current = 0               #当前最长子序列的和
 
  
  for i in range(0, len(arr)):
    #1)当前位置的最长子序列的和有两种可能，分别是下面的if和else
    if max_current + arr[i] >= arr[i]:  
       #第一种可能：到i-1位置和>=0,到i位置的和就是i-1加上当前位置
      max_current = max_current + arr[i]
    else:
      #第二种可能：i-1位置是负数，i位置就是自己的值
      max_current = arr[i]
   
    #2) 如果本轮循环加上i位置的值比上一轮要大，则更新
    #否则不更新(例如本轮加了一个负值，就会比上一轮小，就不要更新)
    if max_so_far < max_current:
      max_so_far = max_current
   
  return max_so_far
 
print (max_subseq_sum(np.array([-2, -3, 4, -1, -2, 1, 5, -3])))
print (max_subseq_sum(np.array([-1,1,2,3,4,-5,2,4])))

上面代码思路说明：

1）分解子问题：

当前位置最长子序列 = Max（当前位置的值，前一个位置的最长子序列和+当前位置的值）

2）存放子问题结果：存放在max_current中

3）本轮结束时会读取子问题的结果max_current，并和上一轮的结果max_so_far比较，选取较大值更新到max_so_far中

算法思路截图：

import sys
# m是硬币的种类，coins代表具体的面值，V是想换取的纸钞面值。 
def minCoins(coins, m, C): 
    # coins: 硬币的面值
    # m : 硬币的个数 = len(coins)
    # C: 需要换的纸币面值
      
    # table[i] 存储换取面值为i的纸币，需要用到的最少量的硬币数
    table = [0 for i in range(C + 1)] 
  
    # Base case 
    table[0] = 0
  
    # 初始化 
    for i in range(1, C + 1): 
        table[i] = sys.maxsize 
  
    # 对于每一种价值i来计算，最少用多少硬币可以换取？
    for i in range(1, C + 1): 
        
        # Go through all coins smaller than i 
        for j in range(m): 
            if (coins[j] <= i): 
                sub_res = table[i - coins[j]] 
                if (sub_res != sys.maxsize and  #在所有coin[j]中找最好的
                    sub_res + 1 < table[i]): 
                    table[i] = sub_res + 1      #上图中m(j)的值+1
    return table[C] 
  
arr = [1, 2, 3] 
m = len(arr) 
n = 6
print(minCoins(arr, m, n))

---

2、吃瓜教程——西瓜书+南瓜书

机器学习中监督学习的基本任务

1. 分类任务
   

2. 回归任务
   

3. 监督学习
   

4. 非监督学习
   

5. 半监督学习
   一部分数据有“标记”或者“答案”，另一部分数据没有 更常见：各种原因产生的标记缺失。

6. 增强学习
   
   知道这些概念后，现在开始步入机器学习的第一步。

2.1 线性回归

---

2.2 逻辑回归

2.2.1 逻辑回归有什么用

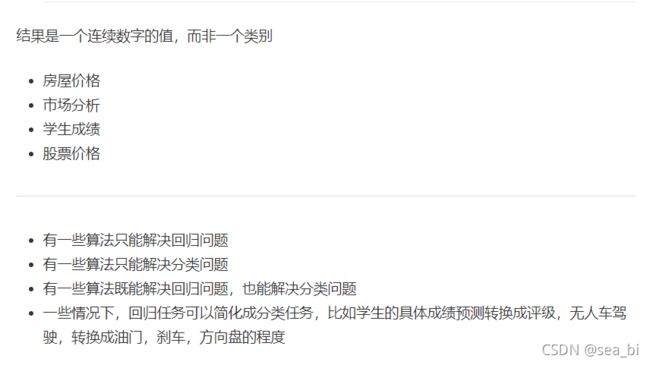
逻辑回归，虽然名字叫“回归”，但是它并不是用来回归的。什么是回归？我们之前有介绍过，回归问题解决的是因变量（即Y）是连续值的情况。
而逻辑回归是解决Y是离散变量的问题，即分类。
通常而言，逻辑回归主要解决的是二分类的问题，即分类的结果只有两个类别。比如【男，女】、【有钱，没钱】、【感染病毒，没感染病毒】、【垃圾邮件，不是垃圾邮件】……等等。
从上面的例子中，我们其实可以想象出，其实逻辑回归的应用场景是比较多的。比如基于邮件的特征，去判断一封邮件是否是垃圾邮件；基于用户行为，判断用户的性别等。

2.2.2 逻辑回归的本质

逻辑回归，虽然是一种分类算法，但确实和“回归”有一些关联。如果用一个公式表达：
逻辑回归=线性回归+sigmoid函数
对，这里的关键，就是sigmoid函数。这个函数就是我们之前讲回归和分类时候的激活函数。激活函数是为了将线性回归的连续性结果映射到离散值上，这样就是分类问题了。

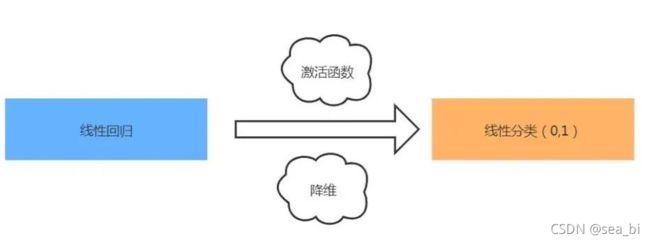
在网上看到一张图展示逻辑回归的原理：

2.2.3 算法逻辑

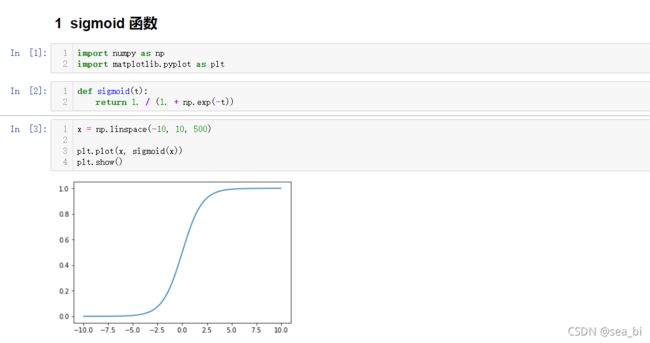
（1）sigmoid函数
我们先看一看下面的函数（单位越阶函数）作为激活函数：

这个是不是可以将连续的z（z=wx+b）映射到离散的y了？是的。
但是，如果将这个函数如果作为激活函数，将会导致函数是不连续不可导的。
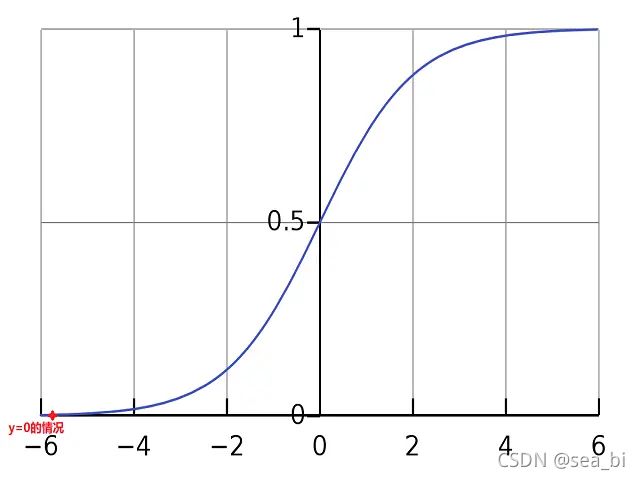
因此，我们需要找到一个可以替代这个函数的函数，使其单调可微。什么函数呢？对，这就是sigmoid函数的一种：对数几率函数。

这个函数是连续的，极限取值是0-1，且可以按照0.5的阈值进行二分类。
用了这个函数以后，y和x的函数关系变为

其中：

2.2.4 损失函数

将输入的值映射到0,1之间，0,1之间就可以看成概率值。
反向传播要求导，求导的结果就是g(z)*(1-g(z))，比较好计算。
红色虚线是求导后函数的图形，当z=0时取最大值0.25；当z取值比较大(两端)，梯度接近为0，这就是神经网络中sigmoid作为激活函数梯度消失的原因。

ok，既然有了上述的预测函数，下一步，我们要定义具体的损失函数。这里，我们通常用对数似然损失来作为损失函数：

这个公式比较好理解，就不展开了。
这个代价函数呢，叫做交叉熵，其中y(i)指的是预测的结果，而hθ(xi)指的是xi这个点原本的值。
那么它具体是什么意思呢，为什么叫做交叉熵？我们举两个极端的例子看看就明白了：
1、xi原始值hθ=1，预测结果，yi=1的情况

这个时候，代价函数的加号右边会被消掉，因为右边（1-y(i)）是0，左边部分呢，因为hθ(xi)=1，故而
log(1)=0。
y(i)log(hθ(xi)) = 1 * log(0) = 0

也就是说，若xi原始值是1，当预测值y=1的时候，代价函数是0的。这个也比较好理解，代价函数为0就是说预测结果和原始结果完全一致的，没有半点出差错。

2、计算结果，yi=0，原始值hθ=0

因为1-hθ(xi)，最终结果还是等于0。
也就是说，这个损失函数，只要原始值与预测结果越相符，损失函数就越大，反之，损失函数就会越小。
以上说的只是一个点的情况，实际的代价函数，是要计算所有点的损失函数的均值，如下所示：

2.2.5 损失函数推导

由于：

假设逻辑回归的cost函数如下，我们如何理解这个公式呢？

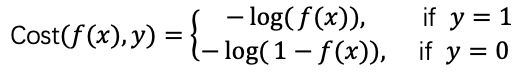
将逻辑回归的cost函数简化，即得出：

所以就有：

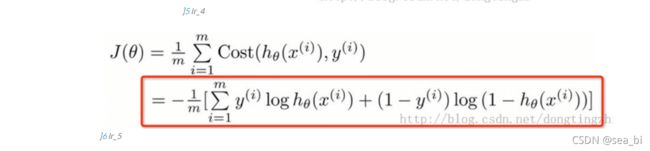
我们可以利用梯度下降算法来求得J(θ)的值最小，根据梯度下降法可得θ的更新过程。j=0 时，代表更新j向量的第0分量，j=1 时，代表更新j向量的第1分量，以此类推，为了方便理解，可以把j看成数组vector_j，j=0，就是更新vector_j[0]。α为学习步长。

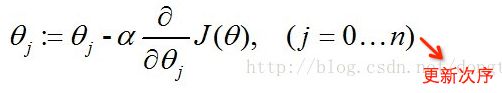
经过一些数学推导的最终形式如下（推导过程为对θ求偏导数）。
针对求导过程：

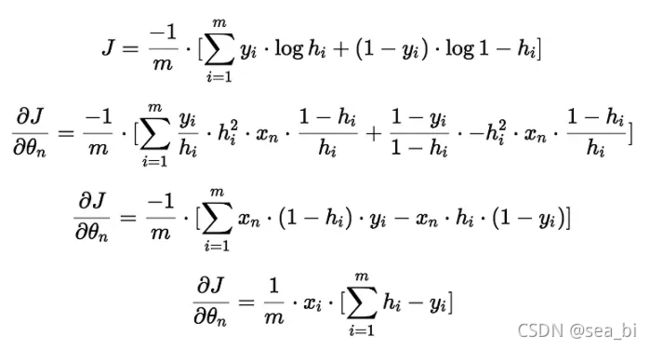
ps：xj为x向量的第j分量，还可以理解为x数组的第j项，其实下图是对θ数组的第j项进行更新的算式，然而真正代码角度是对整个θ数组进行更新，也就是下下图的样子。

当我们把上式向量化处理就得到了代码可以处理的形式。

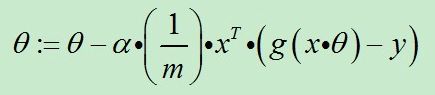
2.2.6 逻辑回归案例

学习了原理之后，看看这个到底怎么使用。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()

X = iris.data
y = iris.target

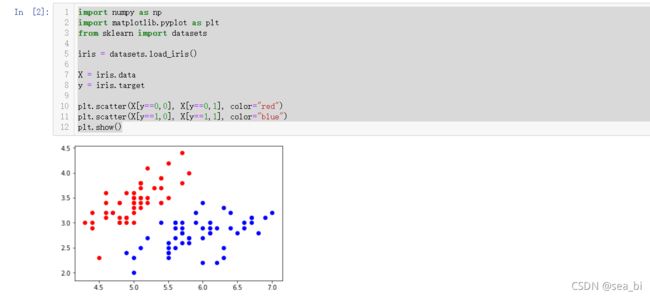
plt.scatter(X[y==0,0], X[y==0,1], color="red")
plt.scatter(X[y==1,0], X[y==1,1], color="blue")
plt.show()

首先对数据进行切分：

import numpy as np
from sklearn import datasets
def train_test_split(X, y, test_ratio=0.2, seed=None):
    """将数据 X 和 y 按照test_ratio分割成X_train, X_test, y_train, y_test"""
    assert X.shape[0] == y.shape[0], \
        "the size of X must be equal to the size of y"
    assert 0.0 <= test_ratio <= 1.0, \
        "test_ration must be valid"

    if seed:
        np.random.seed(seed)

    shuffled_indexes = np.random.permutation(len(X))

    test_size = int(len(X) * test_ratio)
    test_indexes = shuffled_indexes[:test_size]
    train_indexes = shuffled_indexes[test_size:]

    X_train = X[train_indexes]
    y_train = y[train_indexes]

    X_test = X[test_indexes]
    y_test = y[test_indexes]

    return X_train, X_test, y_train, y_test

if __name__=="__main__":
    iris = datasets.load_iris()
    X = iris.data
    y = iris.target
    X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
    print(X_train.shape)  #(120, 4)

接下来编写逻辑回归类：

import numpy as np


class LogisticRegression:

    def __init__(self):
        """初始化Logistic Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def _sigmoid(self, t):
        return 1. / (1. + np.exp(-t))

    def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Logistic Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            y_hat = self._sigmoid(X_b.dot(theta))
            try:
                return - np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(y)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict_proba(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果概率向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return self._sigmoid(X_b.dot(self._theta))

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        proba = self.predict_proba(X_predict)
        return np.array(proba >= 0.5, dtype='int')

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return self.accuracy_score(y_test, y_predict)

    def __repr__(self):
        return "LogisticRegression()"

    # 准确率计算
    def accuracy_score(y_true, y_predict):
        """计算y_true和y_predict之间的准确率"""
        assert len(y_true) == len(y_predict), \
            "the size of y_true must be equal to the size of y_predict"

        return np.sum(y_true == y_predict) / len(y_true)

通过调用进行预测：

import numpy as np
from sklearn import datasets
import LogisticRegression

def train_test_split(X, y, test_ratio=0.2, seed=None):
    """将数据 X 和 y 按照test_ratio分割成X_train, X_test, y_train, y_test"""
    assert X.shape[0] == y.shape[0], \
        "the size of X must be equal to the size of y"
    assert 0.0 <= test_ratio <= 1.0, \
        "test_ration must be valid"

    if seed:
        np.random.seed(seed)

    shuffled_indexes = np.random.permutation(len(X))

    test_size = int(len(X) * test_ratio)
    test_indexes = shuffled_indexes[:test_size]
    train_indexes = shuffled_indexes[test_size:]

    X_train = X[train_indexes]
    y_train = y[train_indexes]

    X_test = X[test_indexes]
    y_test = y[test_indexes]

    return X_train, X_test, y_train, y_test

if __name__=="__main__":
    iris = datasets.load_iris()
    X = iris.data
    y = iris.target
    X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

    log_reg = LogisticRegression()
    log_reg.fit(X_train, y_train)

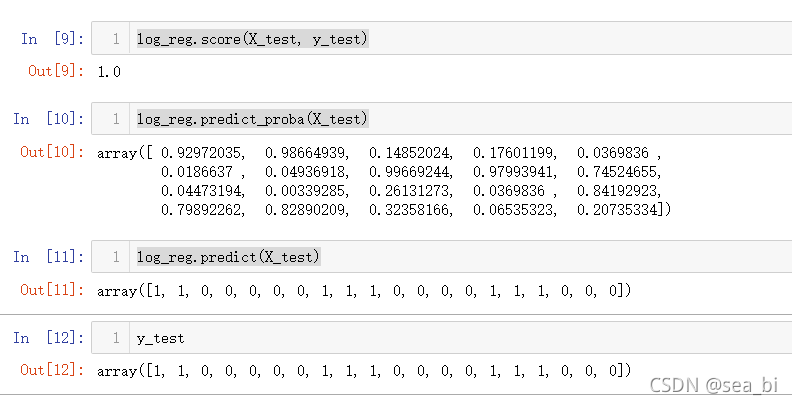
    log_reg.score(X_test, y_test)
    log_reg.predict_proba(X_test)
    print(y_test)

在jupter上展示：

3 Pytorch 深度学习

3.1 numpy

1 保存数组

import numpy as np

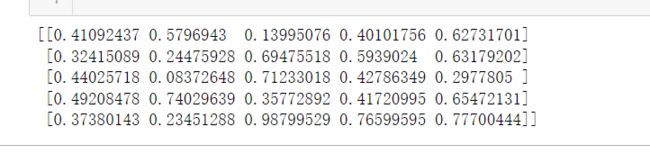
nd9 =np.random.random([5, 5])
np.savetxt(X=nd9, fname='./test1.txt')
nd10 = np.loadtxt('./test1.txt')
print(nd10)

2 numpy数组运算

3 修改数组的形状

4 展平


5 合并数组

6 批量处理

3.2 pytorch基础

1 测试 CUDA

import torch
print("Support CUDA ?: ", torch.cuda.is_available())
x = torch.tensor([10.0])
x = x.cuda()
print(x)

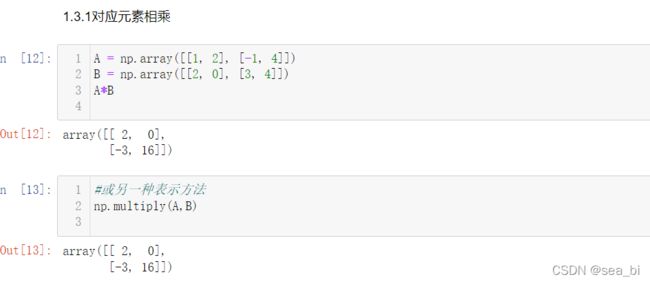
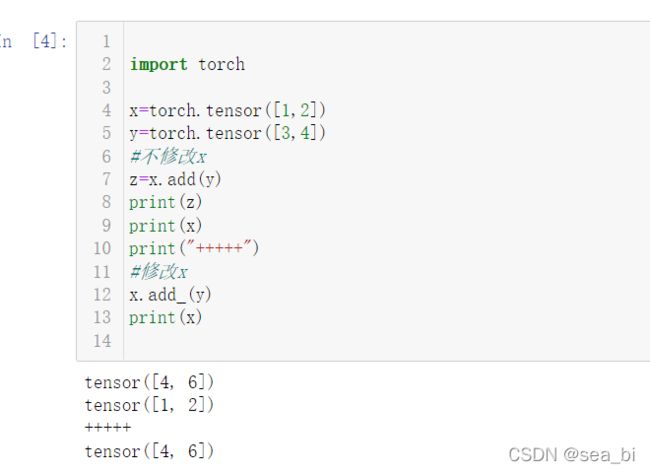
2 add

3 torch.view与torch.reshpae的异同

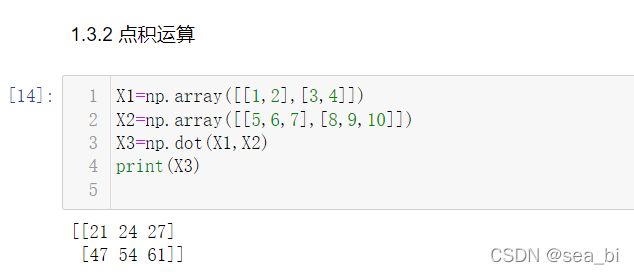
4 矩阵计算


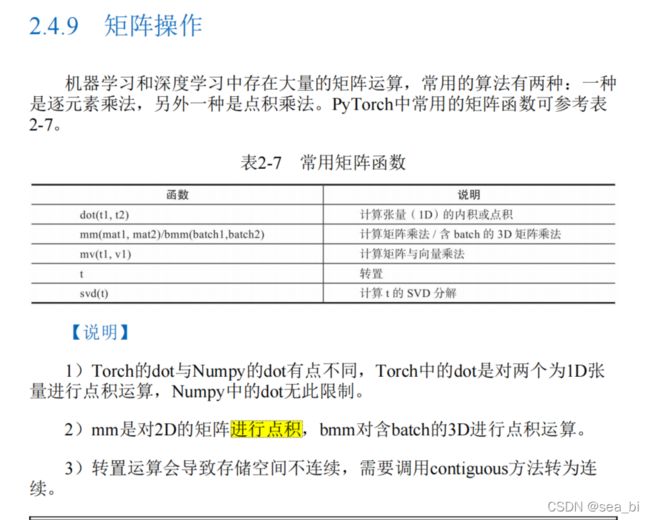
7 对照表

8 求导


9 使用Numpy实现机器学习



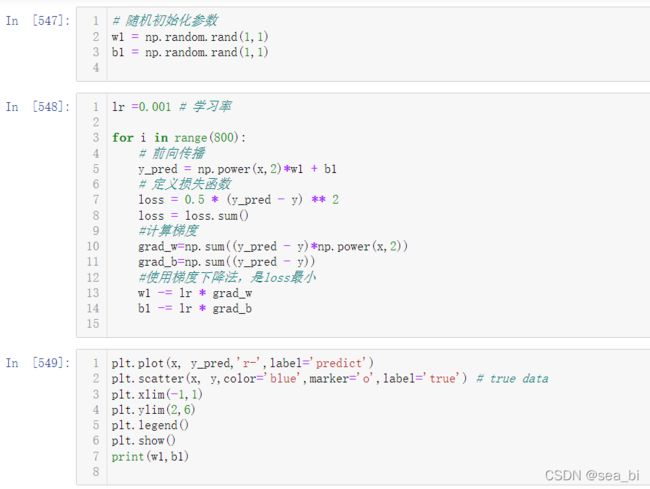
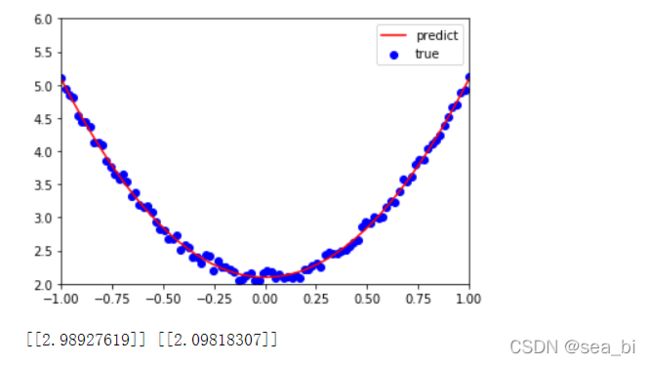
10 使用Tensor及antograd实现机器学习

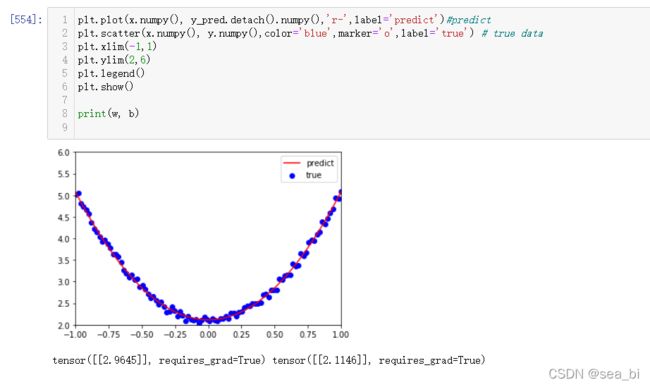
11 使用TensorFlow架构

# -*- coding: utf-8 -*-
import tensorflow as tf
import numpy as np

#生成训练数据
np.random.seed(100) 
x = np.linspace(-1, 1, 100).reshape(100,1) 
y = 3*np.power(x, 2) +2+ 0.2*np.random.rand(x.size).reshape(100,1)  


# 创建两个占位符，分别用来存放输入数据x和目标值y
#运行计算图时，导入数据.
x1 = tf.placeholder(tf.float32, shape=(None, 1))
y1 = tf.placeholder(tf.float32, shape=(None, 1))

# 创建权重变量w和b，并用随机值初始化.
# TensorFlow 的变量在整个计算图保存其值.
w = tf.Variable(tf.random_uniform([1], 0, 1.0))
b = tf.Variable(tf.zeros([1]))


# 前向传播，计算预测值.
y_pred = np.power(x,2)*w + b

# 计算损失值
loss=tf.reduce_mean(tf.square(y-y_pred)) 

# 计算有关参数w、b关于损失函数的梯度.
grad_w, grad_b = tf.gradients(loss, [w, b])

#用梯度下降法更新参数. 
# 执行计算图时给 new_w1 和new_w2 赋值
# 对TensorFlow 来说，更新参数是计算图的一部分内容
# 而PyTorch，这部分是属于计算图之外.
learning_rate = 0.01
new_w = w.assign(w - learning_rate * grad_w)
new_b = b.assign(b - learning_rate * grad_b)

# 已构建计算图, 接下来创建TensorFlow session，准备执行计算图.
with tf.Session() as sess:
    # 执行之前需要初始化变量w、b
    sess.run(tf.global_variables_initializer())


    for step in range(2000):
        # 循环执行计算图. 每次需要把x1,y1赋给x和y.
        # 每次执行计算图时，需要计算关于new_w和new_b的损失值,
        # 返回numpy多维数组
        loss_value, v_w, v_b = sess.run([loss, new_w, new_b],
                                    feed_dict={x1: x, y1: y})
        if  step%200==0:  #每200次打印一次训练结果
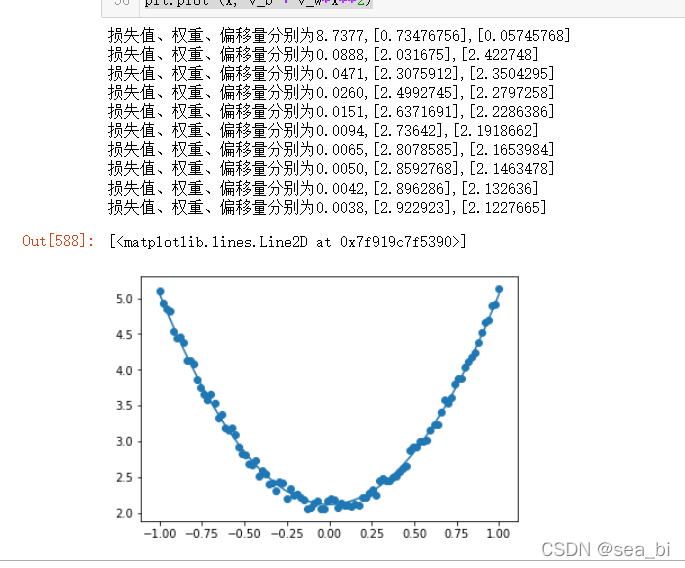
            print("损失值、权重、偏移量分别为{:.4f},{},{}".format(loss_value,v_w,v_b))
# 可视化结果            
plt.figure() 
plt.scatter(x,y)
plt.plot (x, v_b + v_w*x**2)