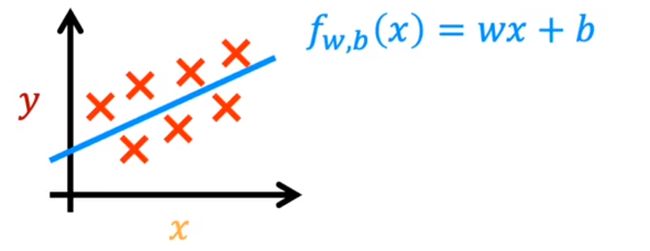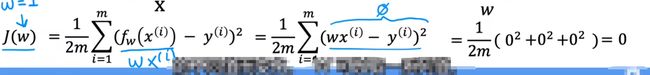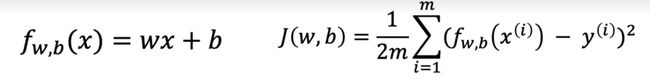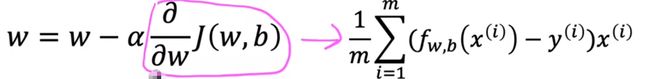第一章:part1监督学习:回归
线性回归(linear regression model)
线性回归模型
回归:可以预测数字作为输出
是一种特殊的监督学习模型
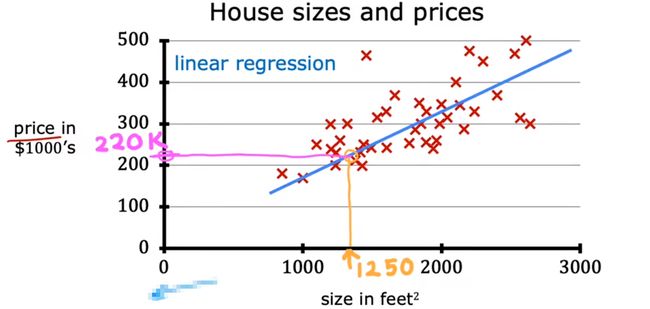
例:通过已知的房价来拟合曲线 可以求得英尺的价格
区别回归与分类:分类的输出结果一般为离散的,并且有限个数
- 术语
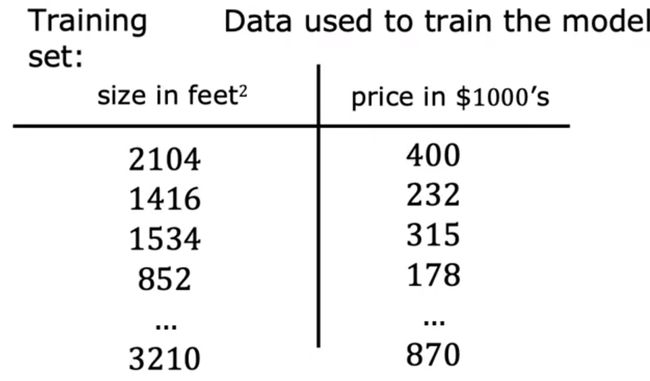
训练集(train set):
输入变量:X(X=2014)
输出变量:Y:(Y=232)
训练样本总数:M
一个训练样本:(X,Y)
( x i , y i ) : i 表示训练集中的第几行 (x^i,y^i):i表示训练集中的第几行 (xi,yi):i表示训练集中的第几行
- 生成规则
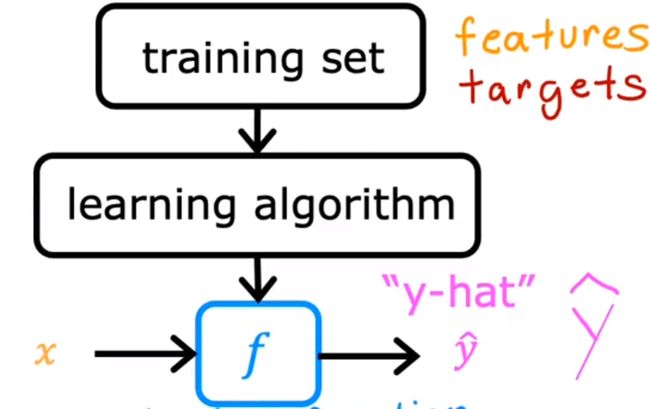
通过训练集获取到一个函数f,它可以通过输入x获得预测的y
y^:被记为预测的y
- f的表示方式
如果默认为直线
f w , b ( x ) = w x + b f_{w,b}(x)=wx+b fw,b(x)=wx+b
生成图像:
只有一个输入变量的线性回归方程
代价函数公式
为了实现回归算法,首先就是要构建代价函数
不同的w与b代表了(输入x的)不同的权值:
不同的w与b会构成不同的函数,我们需要函数尽可能拟合程度更好
代价函数:衡量一条直线与训练数据的拟合程度
m:训练集的样本个数
乘1/2m:为了使后面的方差变小
J ( w , b ) = 1 / 2 m ∑ i = 0 m ( y ^ − y ) 2 :最常用的代价函数公式 J(w,b)=1/2m\sum_{i=0}^{m} (\hat{y}-y)^2:\text{最常用的代价函数公式} J(w,b)=1/2mi=0∑m(y^−y)2:最常用的代价函数公式
即可以写为:
J ( w , b ) = 1 2 m ∑ i = 0 m ( f w , b ( x ( i ) ) − y ) 2 J(w,b)=\frac{1}{2m}\sum_{i=0}^{m} (f_{w,b}(x^{(i)})-y)^2 J(w,b)=2m1i=0∑m(fw,b(x(i))−y)2
理解代价函数
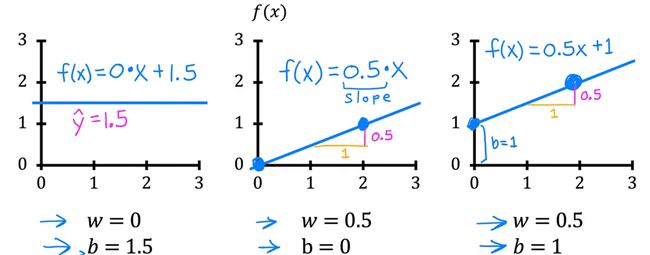
首先,将b=0,观察w是如何影响f(x)与j(w)
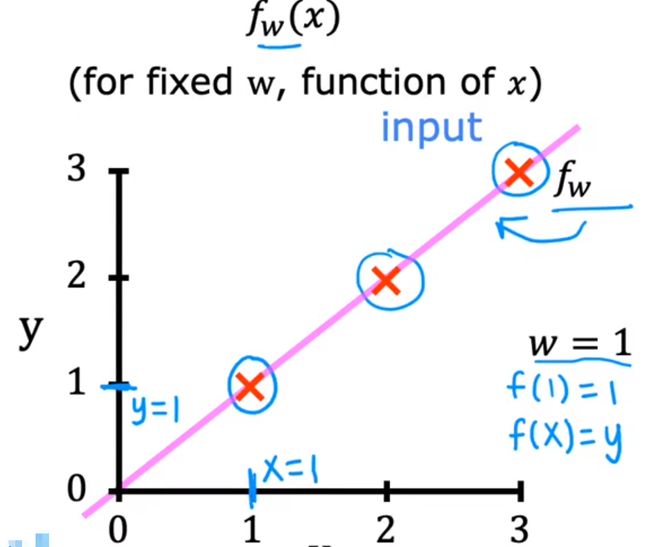
f(x):给定一个w,变量为x
w=1时的图像如下:
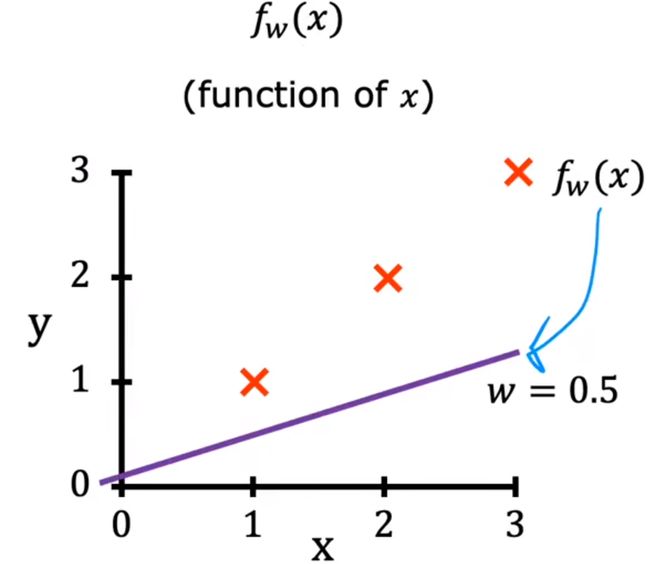
w=0.5图像如下:
j(w):变量为w
通过上图计算不同的j(w)
…
之后根据数值绘制j(w)
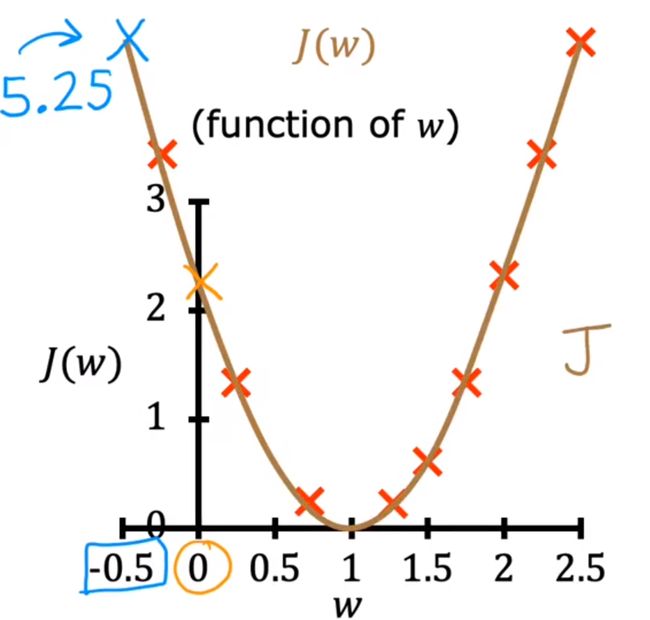
根据图像可知,j(w)越小,函数拟合越好
所以线性回归的目的:找到参数w/b,使得j(w)的值最小
可视化代价函数
观察w,b是如何影响fw,b(x)与j(w,b)
f(x):给定一个w&b,变量为x
w=0.06,b=50时的图像如下:
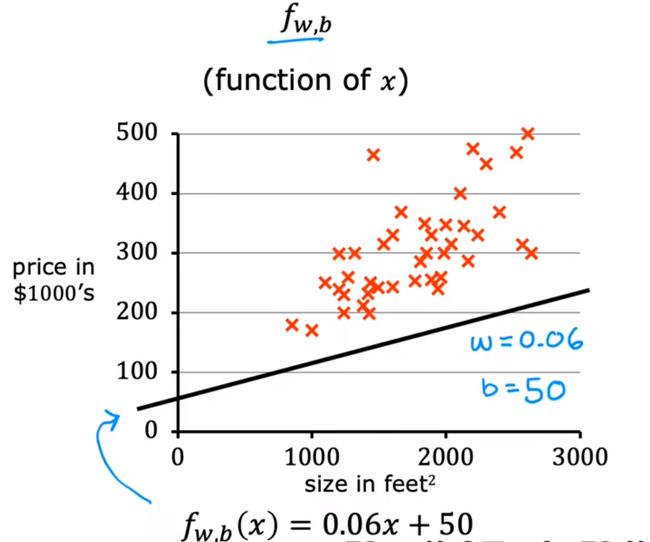
之后根据数值绘制j(w,b):
x轴(b),y轴(w),z轴(J)
可以将上述图像转化为等高线图(二维),中心点为最小值:
例如:取b=800,w=-0.15,代价函数较大
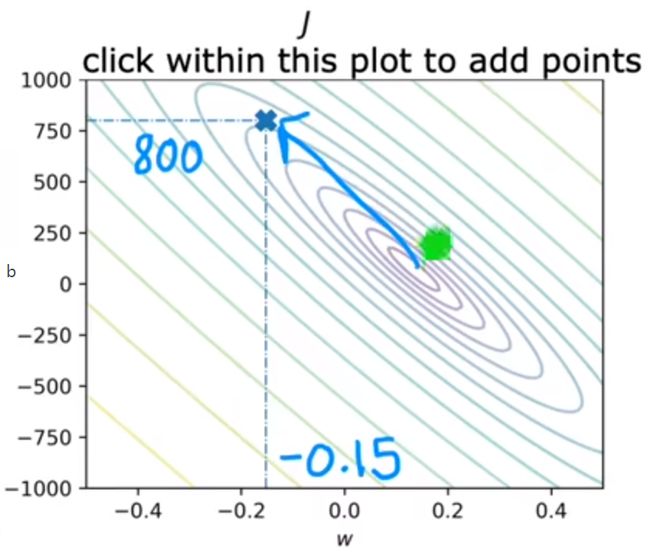
上述取值的拟合函数不太好
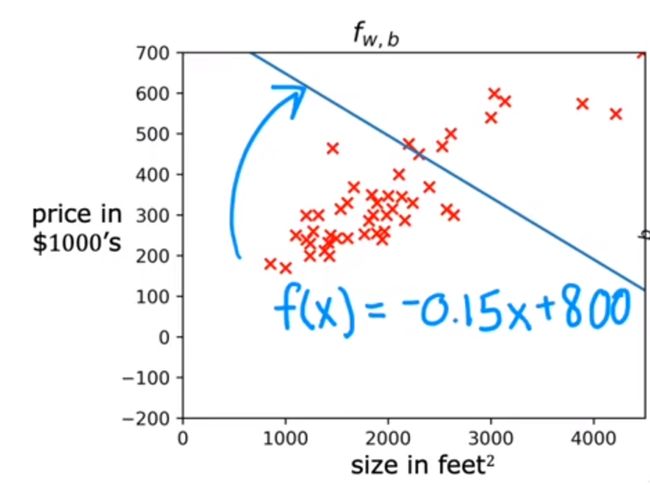
通过以上理解了代价函数是与w与b相关,接下来如何找到w与b使得代价函数最小,该方法为:梯度下降算法
梯度下降
是一种可以最小化任意函数的算法,它可以使函数以斜率下降最快的方式下降
例如下图:模拟一个小人,从J(代价函数)最高点一步步寻找最低点
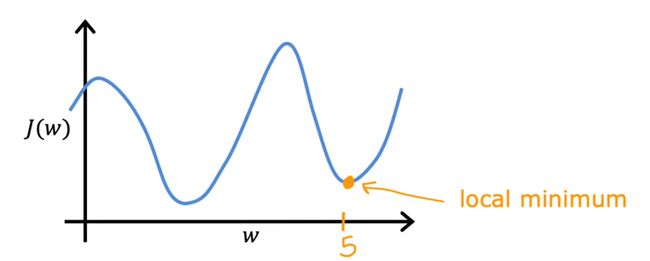
并且选择不同的起点可能找到不同的局部最优解
梯度下降法的实现
- 公式(对于b也同样适用)
α:学习率(0~1),代表下降的幅度
w = w − α d J ( w , b ) d w w=w-\alpha {d{J(w,b)}\over dw} w=w−αdwdJ(w,b)
对当前的w进行微调
d J ( w , b ) d w : 代表从哪个方向下降 {d{J(w,b)}\over dw}:\textcolor{red}{代表从哪个方向下降} dwdJ(w,b):代表从哪个方向下降
注意:w与b的更新需要同步
理解梯度下降算法
可以将b设为0,则代价函数则为一个曲线:
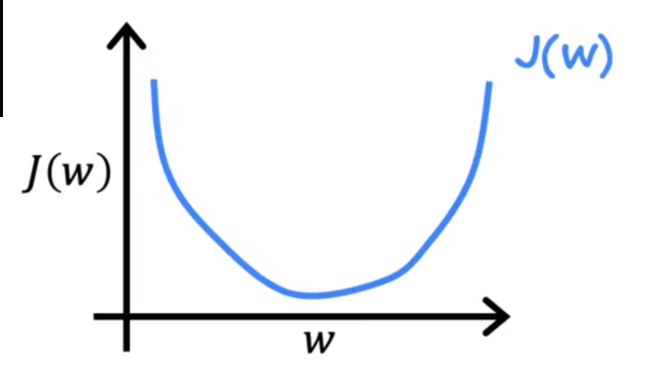
d J ( w , b ) d w : 切线的斜率 {d{J(w,b)}\over dw}:\textcolor{red}{切线的斜率} dwdJ(w,b):切线的斜率
如果斜率为正数,那么w的值会逐渐减小,并且数值向左移动,逐渐接近中间的最小值
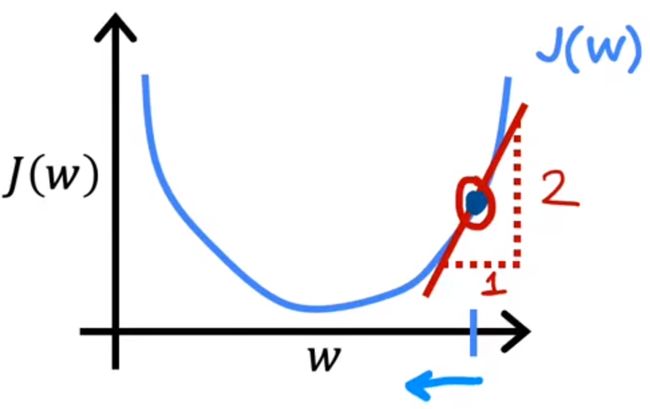
理解学习率α
- 如果学习率过小,那么需要很多步骤才能达到w的最小值点
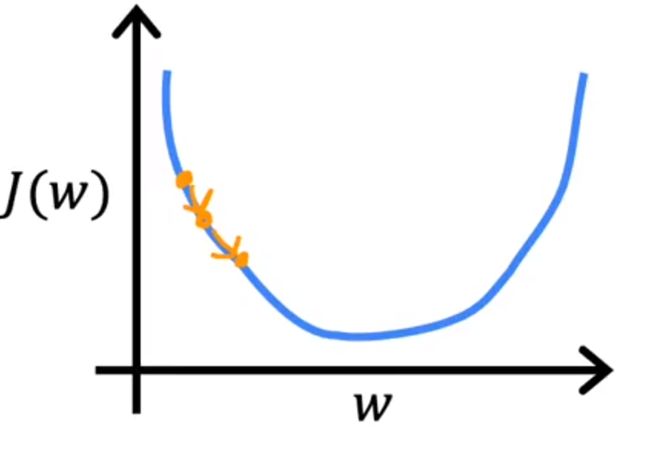
- 如果学习率过大,可能会错过最小值点,或者对于噪声的干扰不强
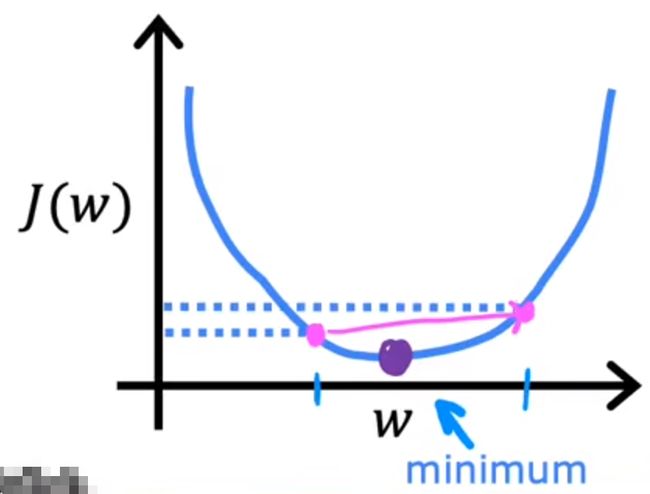
另外,如果梯度下降算法已经到达了一个局部最小值,那么它会终止
因为其在当前的斜率已经为0
用于线性回归的梯度下降
线性回归的默认表达式:
代入梯度下降公式,可得:
下述公式:使用上述的 J(w,b)求偏微分即可
之后可以将该函数代入进行使用
实际模拟图像可以如图所示:
可以看到,给定任意的w与b的值,该方法都会找出代价函数的**局部最小值(拟合局部最好)**来拟合曲线
- 专业词汇
- 批量梯度下降:考虑到全部训练集样本