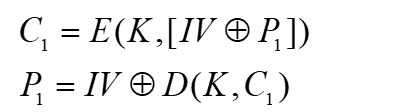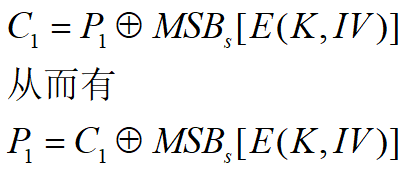网络信息安全基础理论笔记
网络信息安全基础理论
- 安全攻击
-
-
- 被动攻击
- 主动攻击之伪装
- 主动攻击之重放
- 主动攻击之修改
- 主动攻击之拒绝服务
-
- 理论安全和实际安全
-
-
- 理论安全或无条件安全 (Theoretical Secure or Perfect Secure)
- 实际安全或计算上安全 (Practical Secure or Computationally Secure)
-
- 对称密码体制和非对称密码体制
-
-
- 对称密码体制(Symmetric System, One-key System, Secret-key System)
- 非对称密码体制(Asymmetric System, Two-key System, Public-key System)
-
- 序列密码体制和分组密码体制
-
-
- 序列密码
- 分组密码
-
- 其他加密体制
-
-
- 确定型密码体制和概率密码体制
- 单向函数型密码体制和双向变换型密码体制
-
- 分组密码和数据加密标准
- 混淆和扩散 (confusion and diffusion)
- 群, 环和域
-
- 群
-
- 交换群
- 循环群
- 环
- 域
- DES 数据加密标准(Data Encryption Standard)
-
-
- 双重DES (Double DES)
- 三重DES
-
- 分组密码的工作模式
-
- ECB 电子密码本模式(Electronic Codebook)
-
- ECB模式的局限性:
- CBC 密文分组链接模式(Cipher Block Chaining)
-
- CBC的优点和局限
- CFB 密码反馈模式(Cipher FeedBack )
-
- CFB模式的优点和局限:
- OFB 输出反馈模式(Output FeedBack )
-
- OFB的优点和局限
- CTR 计数器模式(Counter )
-
- CTR的优点和局限
- 费马定理
- 欧拉函数φ(n)
-
-
-
- 证明:
-
-
- 欧拉定理
-
-
-
- 证明:
-
-
- CRT 中国余数定理(Chinese Remainder Theorem)
-
- 孙子定理(CRT求解)
- 对称密码体制的问题
- 非对称密码体制的优点
- RSA算法!
-
-
- 算法流程:
- RSA算法满足公开密钥加密的要求, 必须符合下列条件:
- 证明:
-
- 公钥的分配
-
- 公钥的公开发布
- 公开可访问的目录
- 公钥授权
- 公钥证书
- 利用公钥密码分配传统密码体制的密钥
-
- 具有保密性和真实性的会话密钥分配
- Diffie-Hellman密钥交换
- 基于DLP的概率密码系统 (ElGamal Cryptosystem)
- 报文认证或消息认证 (Message Authentication)
-
-
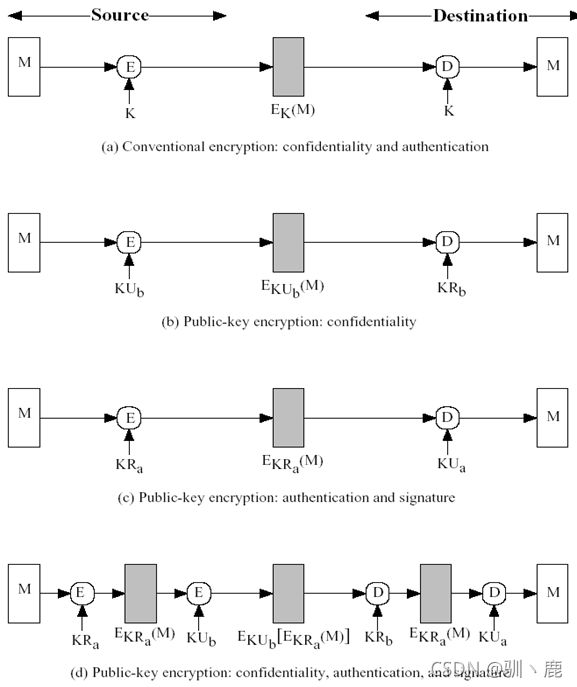
- 1.消息加密
- 2.消息认证码(MAC)
- 3.散列函数 (Hash Function)
-
- 数字签名 (Digital Signature)
-
-
- 数字签名与消息认证的区别:
- 两类数字签名:
- 基于ElGamal的数字签名方法
-
- Kerberos认证
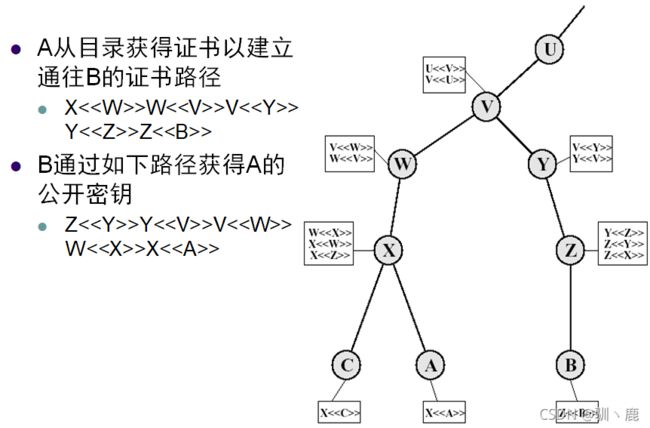
- X.509证书的层次结构 CA
安全攻击
对任何机构的信息资源进行破坏的行为即安全攻击,信息安全就是要检测和防范这种攻击行为,通常threat和attack指的是同样的事情,安全攻击的行为范围很广,通常有两大类安全攻击。
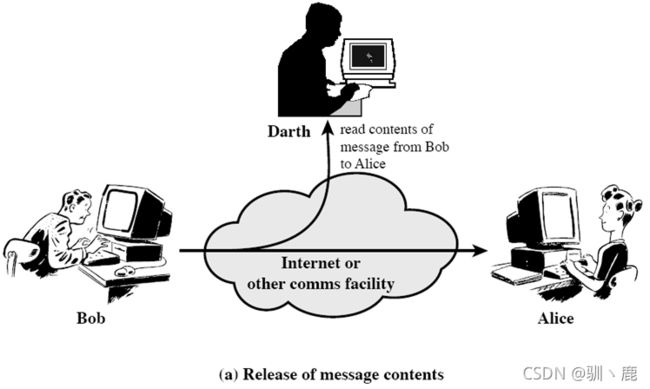
| 被动攻击 | 对传输进行窃听和监测,通信和信息不受影响,用户感觉不到攻击存在,攻击通常是窃听或流量分析,判断通信性质 |
| 主动攻击 | 攻击者破坏通信过程,拦截、修改、伪造、丢弃信息、拒绝服务或假冒合法用户 |
被动攻击
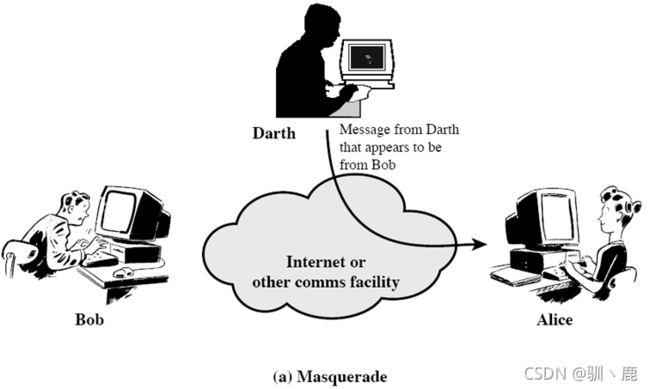
主动攻击之伪装
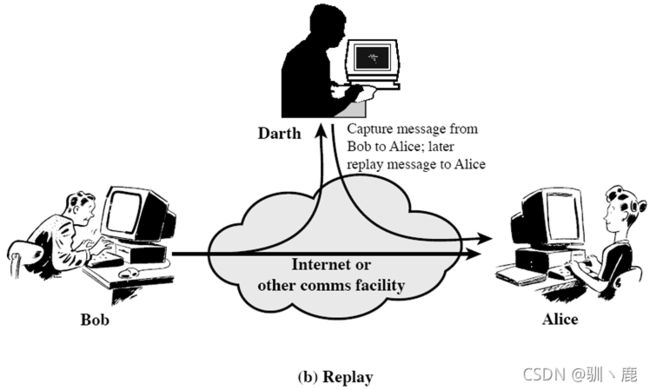
主动攻击之重放
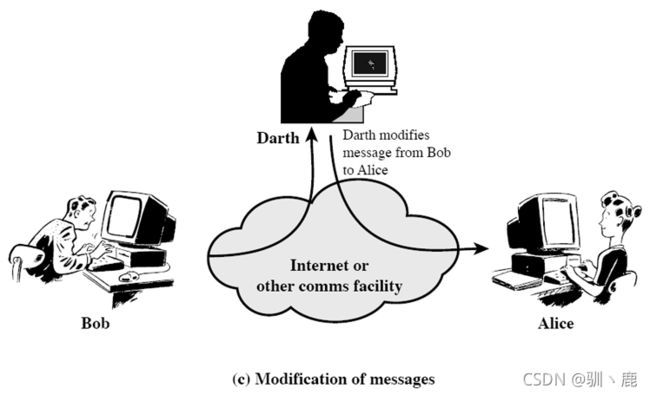
主动攻击之修改
主动攻击之拒绝服务
理论安全和实际安全
理论安全或无条件安全 (Theoretical Secure or Perfect Secure)
攻击者无论截获多少密文,都无法得到足够的信息来唯一地决定明文。欲达理论安全,加密密钥长度必须大于等于明文长度,密钥只用一次,用完即丢,即一次一密,One-time Pad,不实用。
实际安全或计算上安全 (Practical Secure or Computationally Secure)
如果攻击者拥有无限资源,任何密码系统都是可以被破译。但在有限的资源范围内,攻击者都不能通过系统分析方法来破译信息,则称这个安全系统是计算上安全的或破译这个系统是计算上不可行(Computationally Infeasible)。
对称密码体制和非对称密码体制
对称密码体制(Symmetric System, One-key System, Secret-key System)
加密和解密的密钥相同,或者一个密钥可以从另一个导出,加密能力和解密能力是结合在一起的,开放性差。
非对称密码体制(Asymmetric System, Two-key System, Public-key System)
加密和解密的密钥不相同,从一个密钥导出另一个密钥是计算上不可行的,加密能力和解密能力是分开的,开放性好。
序列密码体制和分组密码体制
序列密码
如果密文不仅与最初给定的算法和密钥有关,同时也与明文位置有关(是所处位置的函数),则称为序列密码体制。加密以明文比特为单位,以伪随机序列与明文序列模2加后,作为密文序列。
分组密码
如果经过加密所得到的密文仅与给定的密码算法和密钥有关,与被处理的明文数据在整个明文中的位置无关,则称为分组密码体制。通常以大于等于64位的数据块为单位,加密得相同长度的密文。
其他加密体制
确定型密码体制和概率密码体制
确定型:当明文和密钥确定后,密文也就唯一地确定了。
概率型:当明文和密钥确定后,密文通过客观随机因素从一个密文集合中产生,密文形式不确定,称为概率型密码体制。
单向函数型密码体制和双向变换型密码体制
单向函数型密码体制适用于不需要解密的场合,容易将明文加密成密文,如哈希函数;
双向变换型密码体制可以进行可逆的加密、解密变换。
分组密码和数据加密标准
分组密码是一种加密解密算法,将输入明文分组当做一个整体处理,输出一个等长的密文分组。
许多分组密码都采用Feistel结构,这样的结构由许多相同的轮函数组成。每一轮里,对输入数据的一半进行代换,接着用一个置换来交换数据的两个部分,扩展初始的密钥使得每一轮使用不同的子密钥。
DES是应用最为广泛的分组密码,它扩展了经典的Feistel结构。DES的分组和密钥分别是64位和56位的。
混淆和扩散 (confusion and diffusion)
混淆(confusion):使密文和加密密钥之间的关系尽量复杂。
扩散(diffusion): 明文统计结构扩散消失到大批密文统计特性中,使明文和密文之间统计关系尽量复杂。
群, 环和域
群
群G, 记作{G, •}, 定义一个二元运算•的集合,G中每一个序偶(a, b)通过运算生成G中元素(a•b),满足下列公理:
| 封闭性 | 如果a和b都属于G, 则a•b也属于G. |
| 结合律 | 对于G中任意元素a, b, c,都有a•(b•c)=(a•b)•c成立 |
| 单位元(幺元) | G中存在一个元素e,对于G中任意元素a,都有a•e=e•a=a成立 |
| 逆元 | 对于G中任意元素a, G中都存在一个元素a’,使得a•a’=a’•a=e成立 |
交换群
交换群:还满足以下条件的群称为交换群(又称阿贝尔群)
| 交换律 | 对于G中任意的元素a, b,都有a•b=b•a成立 |
循环群
如果群中的每一个元素都是一个固定的元素a加粗样式 (a ∈G)的幂ak(k为整数),则称群G为循环群。元素a生成了群G,或者说a是群G的生成元。
环
环R, 由{R, +, x}表示, 是具有加法和乘法两个二元运算的元素的集合,对于环中的所有a, b, c, 都服从以下公理:
| 前提条件 | 对于+来说R是交换群 |
|---|---|
| 乘法封闭性 | 如果a和b属于R, 则ab也属于R |
| 乘法结合律 | 对于R中任意a, b, c有a(bc)=(ab)c |
| 乘法分配律 | a(b+c)=ab+ac or (a+b)c=ac+bc |
| 乘法交换律 | ab=ba,交换环 |
| 乘法单位元 | R中存在元素1使得所有a有 a1=1a |
| 无零因子 | 如果R中有a, b且ab=0, 则 a=0 or b=0. |
满足乘法交换律的是交换环;满足乘法单位元和无零因子的交换环是整环
域
域F, 可以记为{F, +, x}, 是有加法和乘法的两个二元运算的元素的集合,对于F中的任意元素a, b, c, 满足以下公理:
| 前提条件 | F是一个整环 |
|---|---|
| 乘法逆元 | 对于F中的任意元素a(除0以外), F中都存在一个元素a-1, 使得aa-1=(a-1)a=1 |
域就是一个集合,在其上进行加减乘除而不脱离该集合, 除法按以下规则定义: a/b=ab-1
有理数集合, 实数集合和复数集合都是域;整数集合不是域,因为除了1和-1有乘法逆元,其他元素都无乘法逆元。
DES 数据加密标准(Data Encryption Standard)
双重DES (Double DES)
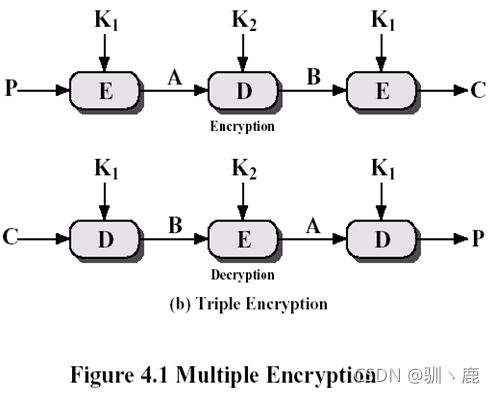
三重DES
分组密码的工作模式
ECB 电子密码本模式(Electronic Codebook)
明文分成64的分组进行加密,必要时填充,每个分组用同一密钥加密,同样明文分组加密得相同密文
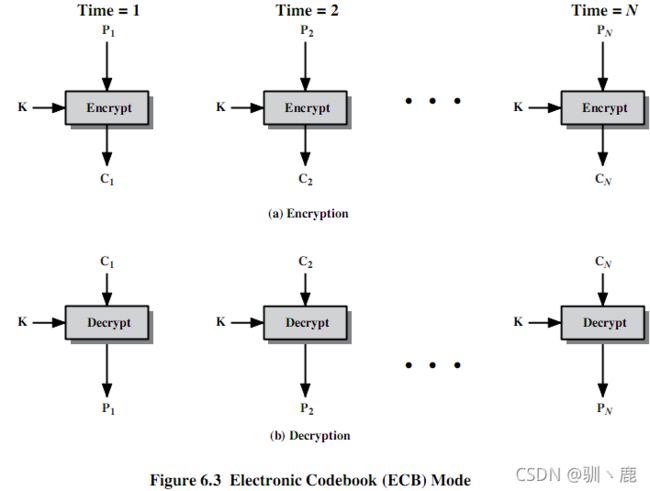
ECB模式的局限性:
| ECB模式特别适合数据较少的情况,如安全传输DES密钥 |
| 一段明文消息中若有几个相同的明文组,则密文也将出现几个相同的片段 |
| 对于很长的消息,ECB是不安全的,如果消息是非常结构化的,密码分析可能利用其结构特征来破解 |
| ECB的弱点来源于其加密过的密文分组是互相独立的 |
CBC 密文分组链接模式(Cipher Block Chaining)
加密输入是当前明文分组和前一密文分组的异或,形成一条链,使用相同的密钥, 这样每个明文分组的加密函数输入与明文分组之间不再有固定的关系
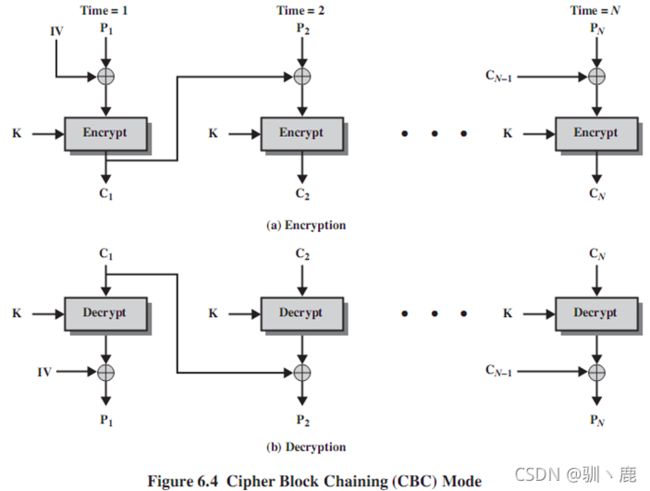
CBC的优点和局限
| 每个密文分组依赖于所有明文分组 |
| 明文消息中的任何一点变化都会影响所有的密文分组 |
| 发送方和接收方需要共享初始向量Initial Value(IV) |
| 如果IV被明文传送,则攻击者可以改变第一分组的某些位,然后预先改变IV中的某些位,则接收者收到的P1也就相应改变了 |
| 因此,IV必须是一个固定的值或者必须用ECB方式在消息之前加密传送 |
| 在消息的最后,还要处理不够长度的分组,可以填充已知非数据值,或者在最后一块补上填充位长度 |
CFB 密码反馈模式(Cipher FeedBack )
是一种将DES转化成流密码的技术,不再要求报文被填充成整个分组,可以实时运行,如果要传输一个字符流,每个字符都可以使用面向字符的流密码加密后立即传输。
加密:加密函数的输入是一个64位的移位寄存器,产生初始向量IV。加密函数高端j位与明文P1的第一单元异或,产生j位密文C1进入移位寄存器低端,继续加密,与P2输入异或,如此重复直到所有明文单元都完成加密。
解密:采用相同方案,但是使用加密函数而非解密函数。
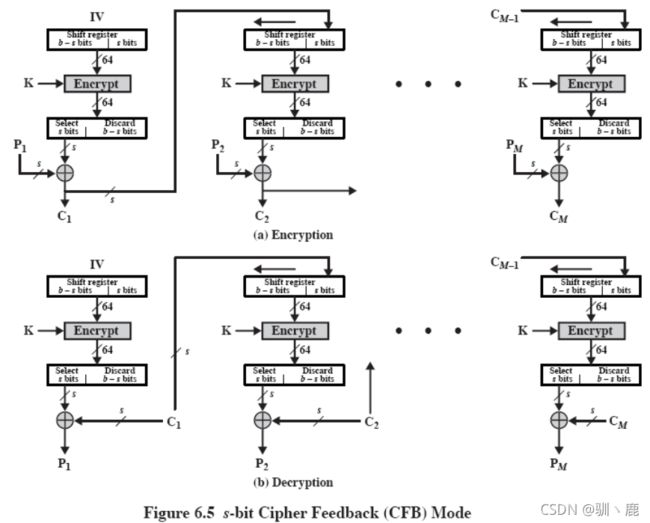
CFB模式的优点和局限:
| 当数据以位或字节形式到达时使用都是适当的 |
| 最通用的是流密码形式 |
OFB 输出反馈模式(Output FeedBack )
结构上类似CFB,但是OFB中加密函数输出被反馈回移位寄存器,CFB中是密文单元被反馈回移位寄存器。优点是传输中的比特差错不会传播,缺点是比CFB更容易受报文流篡改攻击
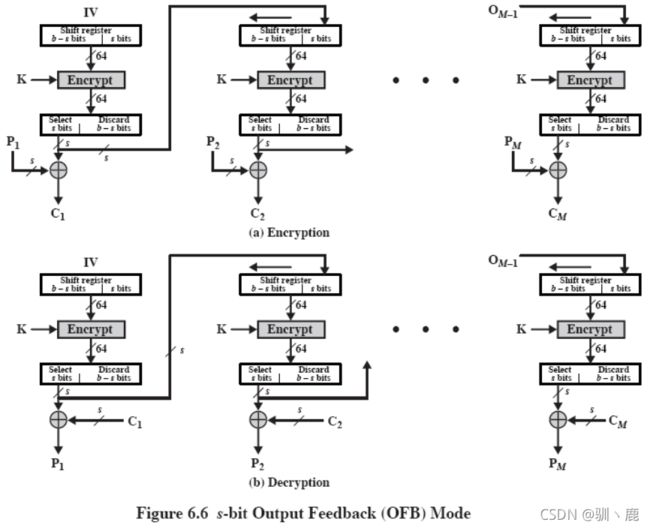
OFB的优点和局限
| OFB的一个优点是传输过程中在某位上发生的错误不会影响到其他位 |
| OFB的缺点是,抗消息流篡改攻击的能力不如CFB |
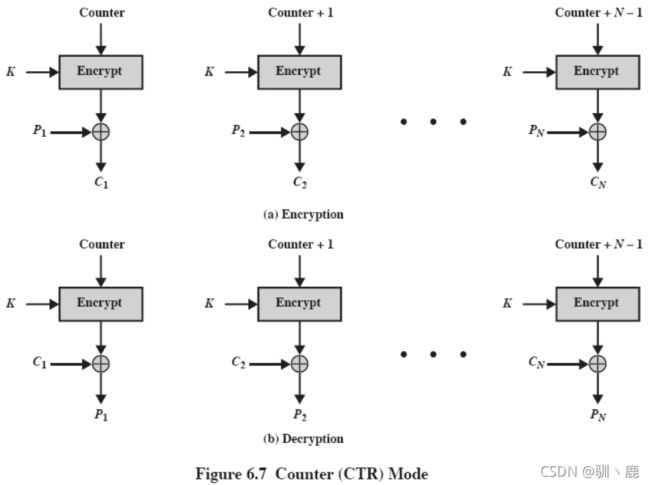
CTR 计数器模式(Counter )
是一种新模式,虽然早就提出来了
与OFB很像,但是加密的是计数器的值而不是任何反馈回来的值
每一个明文分组都必须使用一个不同的密钥和计数器值,决不重复使用
可以用于高速网络加密中
CTR的优点和局限
| 高效 |
| 可以做并行加密 |
| 对高速链路的突发数据加密尤其有效 |
| 可以对被加密的分组进行随机存取 |
| 相当安全 |
| 简洁 |
| 必须决不重复使用密钥和计数器值 |
费马定理
若p是素数, a是正整数且不能被p整除, 则ap-1mod p=1或者apmod p=a.
证明:
因为{a mod p, 2a mod p, …, (p-1)a mod p}是{1, 2, …, (p-1)}的置换形,
所以, (ax2ax … x (p-1)a)≡(1x2x … x(p-1)) (mod p)≡ (p-1)! mod p.
但是, ax2ax…x(p-1)a=(p-1)!ap-1, 因此(p-1)!ap-1≡(p-1)! mod p,
两边去掉(p-1)!, 得ap-1≡1 mod p, 即ap-1mod p=1
置换形证明:
用a乘以集合中所有元素并对p取模,则得到集合
X={a mod p,2a mod p,…, (p-1)a mod p}。因为p不能整除a,
所以X的元素都不等于0,而且各元素互不相等。
假设ja ≡ ka(mod p),其中1≤j
因此X的p-1个元素都是正整数且互不相等。所以说X和
{1,2,…,p-1}构成相同,只是元素顺序不同。
欧拉函数φ(n)
ps:欧拉函数是小于n的正整数中与n互素的数的数目
定理8.2 p和q是素数, n=p*q, φ( n )= φ( p )φ( q )=(p-1)(q-1),显然,对于素数p,φ( p )= p-1
证明:
考虑余数集合{0, 1, …, (pq-1)}中不与n互素的余数集合是{p, 2p, …, (q-1)p}, {q, 2q, …, (p-1)q}和0, 所以
φ( n )= pq-[(q-1)+(p-1)+1]=pq-(p+q)+1= (p-1)(q-1)=φ( p )φ( q )
欧拉定理
证明:
CRT 中国余数定理(Chinese Remainder Theorem)
中国余数定理CRT说明某一范围内的整数可通过它对两两互素的整数取模所得的余数来重构。
Z10(0,1,…,9)中的10个整数可通过它们对2和5(10的素因子,且满足两两互素)取模所得的两个余数来重构. 假设数x(x是Z10中数)的余数r2=0 且r5=3, 即x mod 2=0, x mod 5=3, 则x是Z10中的偶数且被5除余3, 唯一解x=8.

证明:
具体证明如下:
找出所有整数x,使其被3,5和7除时,余数分别为2,3和2
x≡2(mod 3)
x≡3(mod 5)=>x = △ + 357t(△为期中的一个解,t为整数)
x≡2(mod 7)
在同余中最重要的观念就是求出第一个解,那么x = △ + 357t就是通解。那怎么求一个解呢?
利用同余的加性:
把x拆成a+b+c,即x = a + b + c
令
a≡2(mod 3)
a≡0(mod 5)=>a=35p(可以看到p取1的时候满足a≡2(mod3),即a=35)
a≡0(mod 7)
接下来要求b:
b≡0(mod 3)
b≡3(mod 5)=>b=21q(可以看到q取3的时候满足b≡3(mod5),即b=63)
b≡0(mod 7)
求c
c≡0(mod 3)
c≡0(mod 5)=>c=15m(可以看到m取2的时候满足c≡2(mod7),即c=30)
c≡2(mod 7)
得
x≡2(mod 3) ≡ a + b + c
x≡3(mod 5) ≡ a + b + c
x≡2(mod 7) ≡ a + b + c
a b c 都求出来之后,可以利用同余的加性
x = a + b + c = 128是一个解,x = 128 + 105t 在适当调整t之后就可以求出x在任何范围内的解,比如说求最小正整数解,这时候t取-1,得x=23
引用CSDN用户Rain722.
孙子定理(CRT求解)
对称密码体制的问题
| 加密能力与解密能力是捆绑在一起的 |
| 密钥更换、传递和交换需要可靠信道,密钥分发困难 |
| 如有N用户,则需要C=N (N-1)/2个密钥,n=1000时,C(1000, 2)≈500000, 密钥管理困难 |
| 无法满足不相识的人之间通信的保密要求 |
| 不能实现数字签名 |
非对称密码体制的优点
公开密钥密码系统具有: 保密性和认证性
| 加密能力与解密能力是分开的 |
| 密钥分发简单 |
| 需要保存的密钥量大大减少,N个用户只需要N个密钥 |
| 可满足不相识的人之间保密通信 |
| 可以实现数字签名 |
RSA算法!
算法流程:
随机选择两个秘密大素数p和q;
计算公开模数n=p*q;
计算秘密的欧拉指数函数φ(n)=(p-1)(q-1);
选择一个与φ(n)互素的数,作为e或d;
(e,n)是公开的
用Euclid算法计算模φ(n)的乘法逆元素,即根据ed mod φ(n)=1, 求d或e;
加密:C = Me mod n
解密:M= Cd mod n = (Me mod n)d mod n = M
RSA算法满足公开密钥加密的要求, 必须符合下列条件:
有可能找到e, d, n的值, 使得对所有M
对于所有M
在给定e和n时, 计算d是不可行的
几个关系
φ( n ) = φ( pq )=φ( p )φ( q )=(p-1)(q-1),p,q是私密的
ed mod φ( n )=1, ed = kφ( n )+1, 即ed≡1 mod φ( n ), d≡e-1 mod φ( n )
证明:
定理:给定ed mod φ(n) =1, m∈[0, n-1], gcd(m, n)=1, 则:
(me mod n )d mod n = med mod n = m
公钥的分配
| 几种公钥分配方法 |
|---|
| 1. 公开发布 |
| 2.公开可访问的目录 |
| 3.公钥授权 |
| 4.公钥证书 |
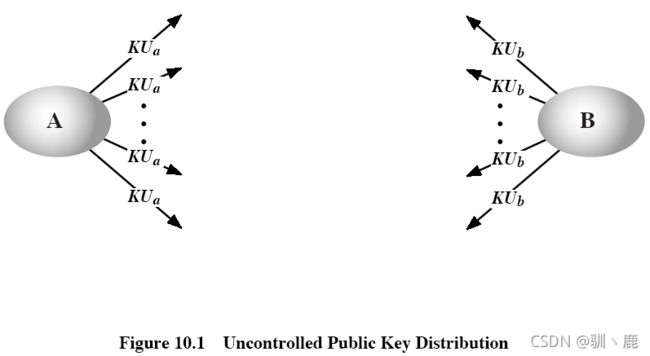
公钥的公开发布
用户将他的公钥发送给另一通信方,或者广播给通信各方,比如在电子邮件后附上PGP密钥,或者发布到邮件列表上。
最大问题在于任何人都可以伪造这种公钥的发布
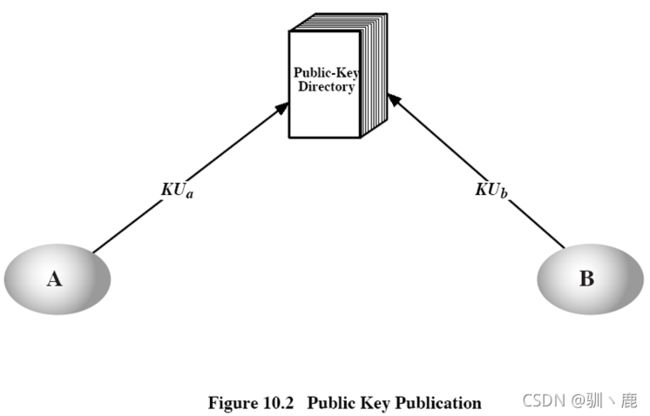
公开可访问的目录
维护一个动态可访问的公钥目录可以获得更大程度的安全性
一个可信实体或组织负责这个公开目录的维护和分配:
----------------------目录包含{name, public-key}等项
----------------------每一通信方通过目录管理员以安全的方式注册一个公钥
----------------------通信方在任何时刻可以用新的密钥替代当前的密钥
----------------------目录定期更新
----------------------目录可通过电子方式访问
一旦攻击者获得目录管理员私钥,则可传递伪造的公钥,可以假冒任何通信方以窃取消息,或者修改已有的记录
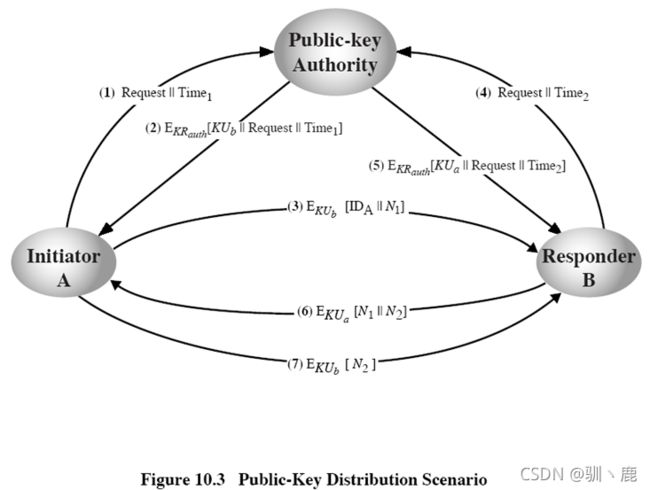
公钥授权
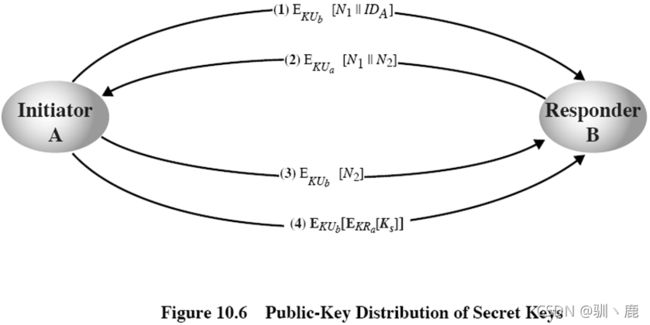
A发送带有时间戳的消息给公钥管理员, 请求B的当前公钥
管理员给A发送用其私钥KRauth加密的消息, A用管理员的公钥解密,可以确信该消息来自管理员:
————B的公钥KUb,用来加密;
————原始请求,A可以验证其请求未被修改;
————原始时间戳, A可以确定收到的不是来自管理员的旧消息。
A保存B的公钥, 并用它对包含A的标识IDA和Nonce1的消息加密, 然后发送给B
B以同样方式从管理员处得到A的公钥
B用KUa对A的N1和B的N2加密, 发送给A
A用B的KUb对N2加密并发送给B, 使B相信其通信伙伴是A
公钥证书
有了公钥证书使得不通过实时访问公钥授权部门而实现公钥交换成为可能
公钥证书将一个通信方的身份与他的公开密钥绑定在一起,通常还包括有效期和使用方法等
证书的所有内容必须经由可信公钥授权方或者证书授权方签名后方可生效
知道公钥授权当局公开密钥的任何人都可以验证一个用户的公开密钥证书的有效性
对于申请者A,管理员提供的证书为:
CA = EKRauth [T, IDA, KUa]
其他人读取并验证:
DKUauth[CA]=DKUauth [EKRauth [T, IDA, KUa]]=(T, IDA, KUa)

利用公钥密码分配传统密码体制的密钥
采用前述方法获得的公开密钥可以用于保密和认证之需。公钥密码算法速度较慢,更适合作为传统密码中实现秘密密钥分配的一种手段。因此,需要产生会话密码来加密。已经有一些方法用来协商适当的会话密钥
具有保密性和真实性的会话密钥分配
Diffie-Hellman密钥交换
基于DLP的概率密码系统 (ElGamal Cryptosystem)
这里特别注意,k不能重复使用,如果
(1) c1,1 =αkmod p c2,1 = m1K mod p
(2) c1,2 = αk mod p c2,2 = m2K mod p
得:m1/m2 = c2,1/c2,2 mod p. 如果m1已知,m2即可算出。
ElGamal密码体制是概率密码体制,同样的明文每次加密得到不同的密文, 因为每次随机选择k。
ElGamal密码体制加密效率是50%,因为密文大小是明文的两倍。


报文认证或消息认证 (Message Authentication)
| 三种消息认证的方法: |
|---|
| 1.消息加密 |
| 2.消息认证码(MAC) |
| 3.哈希函数 |
1.消息加密
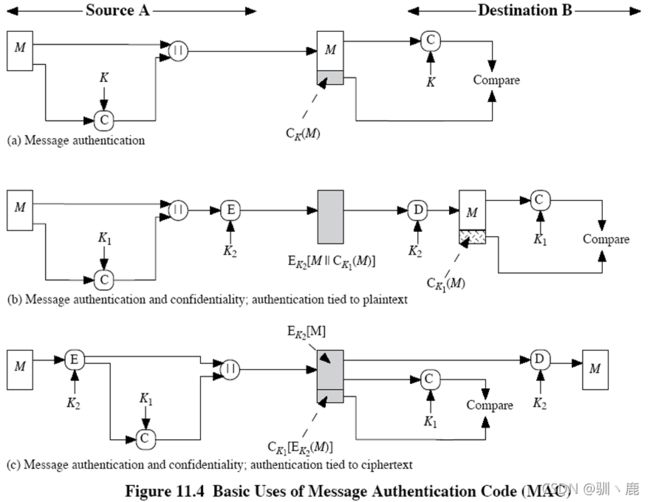
2.消息认证码(MAC)
MAC消息认证码的特点:
MAC加密所得的消息校验和MAC = CK(M)
使用一个秘密密钥K,浓缩一个变长的消息M,产生一个固定长度的认证子
MAC是一种多对一的函数,定义域由任意长的消息组成,值域由所有可能的MAC和密钥组成。若使用n位长的MAC, 则有2n个可能的MAC, 有N条可能的消息, N>>2n. 若密钥长度为k, 则有2k种可能的密钥。
如N为100, n为10, 共有2100不同的消息, 210种不同的MAC, 平均而言同一MAC可由2100/ 210=290条不同的消息产生。若密钥长度为5,则从消息集合到MAC值的集合有25=32不同映射。
MAC函数类似加密,但非数字签名,也无需可逆
由于认证函数的数学性质,与加密相比,认证函数更不易被攻破
MAC不提供数字签名,因为双方共享密钥
3.散列函数 (Hash Function)
一个散列函数以变长的报文M作为输入,产生定长的散列码H(M),作为输出,亦称作报文摘要Message Digest。散列码是报文所有比特的函数值,具有差错检测能力,报文任意一比特的改变都将引起散列码的改变,加密过程很慢,硬件开销大。应用在数字签名上的哈希函数必须是强哈希函数
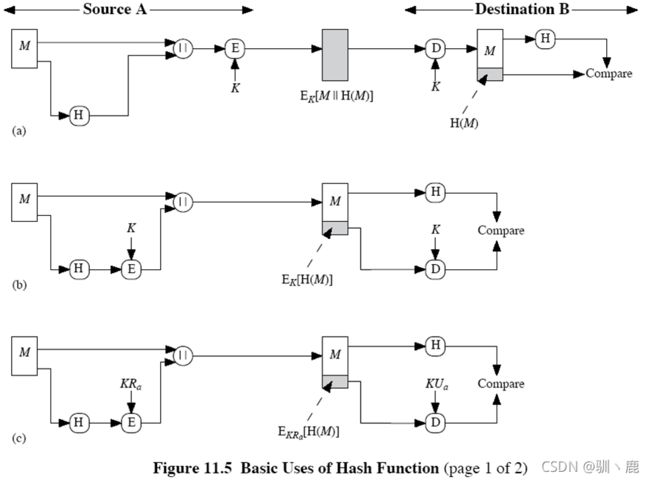
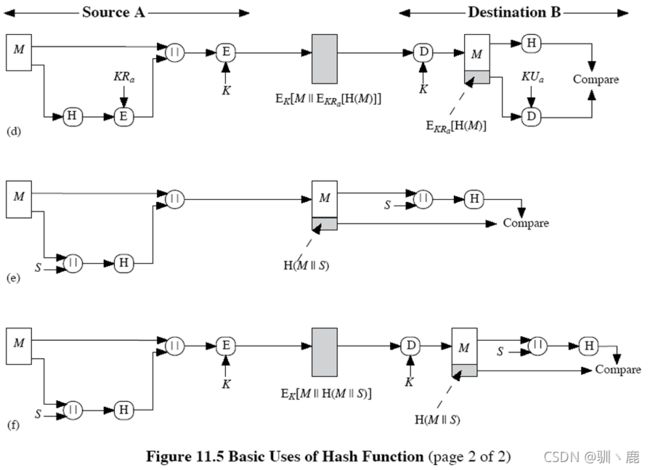
| 对散列函数h=H(M) 的要求: |
|---|
| 1. H可以应用于任意大小的数据块 |
| 2. H产生固定长度的输出 |
| 3. 对任意给定的明文x,计算h=H(x)容易,可由硬件或软件实现 |
| 4. 对任意给定的散列码h,找到满足H(x)=h的x,在计算上不可行,单向性 |
| 5. 对任何给定的分组x,找到满足y≠x且H(x)=H(y)的y,在计算上不可行,抗弱碰撞性,称弱哈希函数 |
| 6. 找到任何满足H(x)=H(y)的偶对(x, y),在计算上不可行,抗强碰撞性,称强哈希函数 |
数字签名 (Digital Signature)
数字签名的简单定义:
数字签名是使以数字形式存储的明文信息经过特定密码变换生成密文,作为相应明文的签名,使明文信息的接收者能够验证信息确实来自合法用户,以及确认信息发送者身份。
| 对数字签名的基本要求 |
|---|
| 在收发双方不能完全信任的情况下,需要除认证之外的其他方法来解决假冒和否认的问题,数字签名则是解决办法 |
| 签名接收者能容易地验证签字者对消息所做的数字签名,包括日期和时间 |
| 任何人,包括签名接收者,都不能伪造签名者的签字 |
| 发生争议时,可由第三方解决 |
数字签名与消息认证的区别:
消息认证是使消息接收方验证消息发送者发送的内容有无被修改过,对防止第三者破坏足够,但收发双方有利害冲突时就无法解决纷争,需要更严格的手段,即数字签名。
对消息签名的两种方法:
1.对消息整体的签字,将被签消息整体经过密码变换得到签字;
2.对消息摘要的签字,附在被签消息之后,或嵌在某一特定位置上作一段签字图样。
两类数字签名:
确定性数字签名,明文与签名一一对应;
概率性数字签名,一个明文可以有多个合法签名,每次都不一样。
基于ElGamal的数字签名方法
若A为B签署m,0<= m <= p-1,
A随机选择k∈[0, p-1],gcd(k, p-1) = 1
计算r =αk mod p
计算αm ≡ YArrs mod p, YAαxAmod p
即αm ≡αxAr αks mod p
则 m = (xA r + ks) mod (p-1)
根据此式求s,则对于m的数字签名即为(r, s),
0≤ r, s
αm mod p = YArrs mod p, 看其是否一致, k不能重复使用。

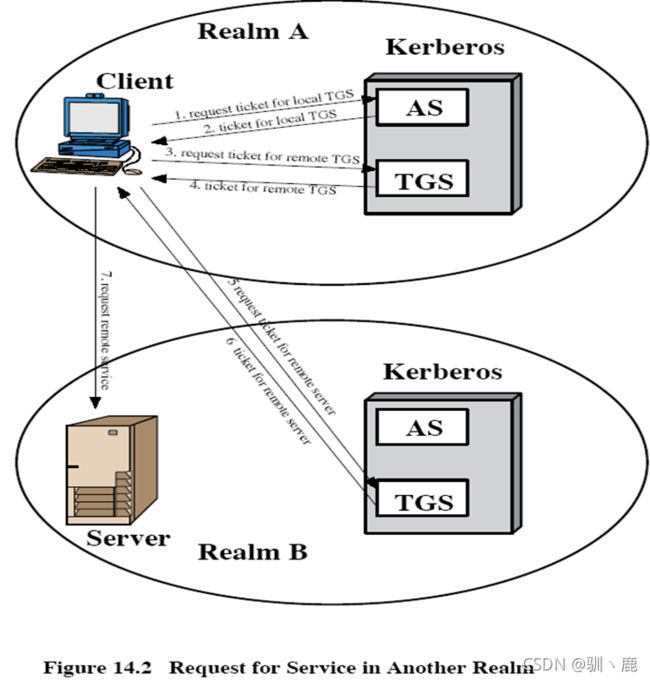
Kerberos认证
TS:时间戳
Lifetime:有效时间
Ticket:票据

跨域连接