2018石中大集训线段树总结.。。。

8/1 线段树练习总结——谢鹏宇

PS：题目见底部。。。

A - I Hate It

 就是一道模板题，但是还是提交了很多次，评测机可能对STD的max函数有点误解，用STD的就会错，然后自己手写了一个三目运算max。可能是因为数据问题，然后刚好卡过去。。。

B - A Simple Problem with Integers

      第二题也是一道模板题。错在维护的时候，标记要累加，但是我覆盖了标记，所以导致错误。。

C - Naive Operations

    题意：给你a,b两个序列，a一个初始值为空的序列，然后输入b序列的一个排列，对a序列进行区间加操作[l,r]，然后询问区间[l,r] ，返回的结果是a[l]/b[l]+a[l+1]/b[l+1]+a[l+2]/b[l+2]+……+a[r]/b[r] (其中除法是下取整例如：1/2=0)

思路:其实这是一道数学题，线段树只是一个辅助运算工具罢了，要点还是去证明为什么用线段树不会超时。我们一步一步分析，1 当a/b的时候，因为是下取整，所以只有当a是b的倍数的时候才会对a/b有影响，当我们用线段树进行区间加的时候怎么知道a是不是b的倍数呢？（1）一个一个查询，这样时间复杂度很高，根本就不需要线段树了。（2）当a是b的倍数的时候，是不是a=若干个b相加，我们就可以把问题转化为：a从0加到b，一加到b就标记a/b的值要加1，然后再把a清零，不断做这种操作。我们这样子做只不过是把理解问题的方式简化了，但是处理问题还是很麻烦，你怎么知道它什么时候加到b呢？我们这个时候就嵌套上线段树，线段树可以求和，求最大值，求最小值，我们怎么知道它能够加到b？可以换个思维想问题，因为b序列中每个数的大小不一，所以他们到达的边界也不一，如果反过来，a从0加到b其实就是a从b减到0，这样序列中的每个数的边界都统一是0了，就用线段树去维护最小值。。这个时候如果最小值是0，你就能够知道这段区间里面有某个数达到了对应的b，这段区间的答案就需要加1了（a==b所以这段区间的a/b的值又大了1）。但是想想，这样子做你要一次性把所有零取出来，然后给区间的答案加上v （v个0） 然后再把对应的0的位置的数变回b才能再往下减。这样子暴力去做会不会超时呢？？这就需要数学证明了，有Q次询问，假使答案是g的话，那么你找到的0也就总计有g个，我们先来算算这个g，肯定是每次都add（1，n）的区间是使得g最大的那么有Q次加法，g=(Q/1+Q/2+Q/3+Q/4+Q/5+……+Q/n) =Q(1+1/2+1/3+1/4+1/5……+1/n) ,然后有详细的证明出(1+1/2+1/3+1/4+1/5……+1/n)是约为logn的所以g=Qlogn，也就是有Qlogn个0，也就只需要暴力修改Qlogn次这样子就不会超时了。所以一步步总结下来：线段树存两个值，一个是最小值，一个是区间的价值，然后把a序列初始化为b序列，然后对应的add其实是对每个a序列进行减操作，如果发现最小值==0就logn进去修改这个数，然后对应所属的区间的价值就要加。然后询问的时候直接求和，把对应的价值加起来。。。

从中学到了两个重要的东西：（1）转换法，本来是a从0到b，然后转化成a从b到0，达到一个目标：共同的边界。。（2）分析法，分析0的个数，从而反应到暴力修改的次数，从而去推测时间复杂度。

D - 约会安排

这个题目非常杂乱，要先自己提取有用的信息，看他要你干什么事情。。。以后看到这种题目，可以尝试模拟，把它复杂的问题归纳下来自己想一个好理解的，好思考的问题嵌套上去。。这道题其实就是G的升级版，因为这里有两个量，女神和基友，所以就要开两棵线段树，在第一棵找完之后去第二棵找，然后必要的修改，两棵树一起修改。。但是线段树维护的内容和怎么去维护详情见题G

E - Stars in Your Window

     题意：一个平面空间，有很多颗星星，每颗星星有自己的权值V，现在有一个矩形，要用这个矩形去框住某些星星使得他们的权值和最大

这是一道经典的扫描线题目，通过这一题其实也深入学习了扫描线。我们先看，为什么这道题要怎么做。如果是单纯的二维前缀和的话（1）会爆数组，没有这么大的数组，（2）会超时，n*m很大。但是我们会发现其实星星的总数是很小的，这就是一个突破口，然后就可以联想到扫描线。

扫描线是什么？？（我的理解如下）

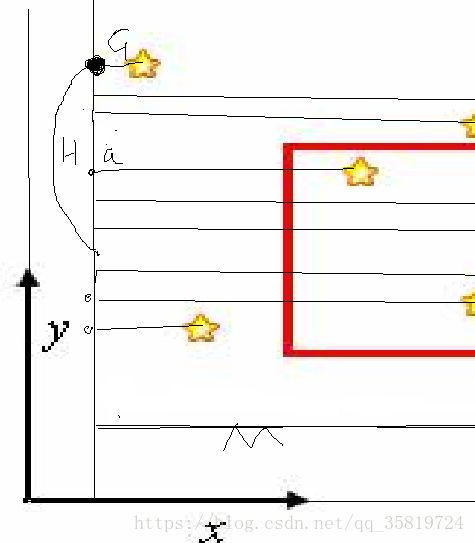
这里有两根扫描线，a和b然后他们之间是保持着距离为m（同时m就是去覆盖星星的矩形的长）然后不断地向右移动。那这样子有什么用呢？

把每颗星星向扫描线a作垂直，得到的点代表着这个星星的位置。这样我们就把这个二维的平面给压缩成了一条线，就把二维给转化成了一维，然后我们现在的任务就是去维护这条线a对吧。我们看

对于这个点G来说，（PS：H是去覆盖星星的矩形的高），把G作为右上角的话，能提供贡献的区间的高就是y[G]——y[G-H+1]，每一个星星在扫描线a上都会有对应的提供贡献的区间，然后我们就需要把它提供的贡献（他的权值）给加入到这个区间然后维护区间和。这样就能够保证从这条线中的某个点取出的整条线的最大值a一定是只能被H覆盖的高的和（在这个区间的所有星星的y坐标中（abs(max[y]-min[y])<=H的）。因为我们要求的是全局的权值最大，所以扫描线a维护的同时也有一个区间最大值。然后有这些操作，我们就可以选取线段树来进行维护。我们现在处理完了扫描线a，同时ab两条线是在不断地往右移动，

如图:

在某个时刻，可能A’这颗星星就会进入到ab两条线这个区间，当A’一进去的时候就需要在扫描线a维护的这棵线段树中区间加操作，竟然移动的话，肯定在某一时刻星星G又会出去ab两条线这个区间，然后我们就要对这个区间进行区间减操作，然后一直这样子维护下去。但是在某些题目中，可能坐标是浮点数，或者很大，超出了空间限制，我们就要对点进行离散化，因为这些点之间虽然隔了很多，但都是对答案不存在影响的空点，通过离散，标记距离和当前点影响的区间，这样线段树就可以很好地实现功能了。

F - Mayor's posters

题意：有n张壁纸，然后贴到一个墙上，它的左边的起点l，和右边的终点r，然后按照输入顺序贴，问最后能够在第一层看到多少种壁纸。

思路：其实很简单，就是直接覆盖上去，区间覆盖，墙很长，壁纸数很小，所以可以先离散后，放入到线段树里，进行覆盖操作。

G - Hotel

 题意：就是有一堆奶牛按顺序来到一个宾馆，宾馆有n间房子，这一堆奶牛需要第一个连续的一段长度为d的空房间，有的话就要住进去，不然就会走人。每次询问要输出那一段的起点，如果住不进去就输出0，然后还有一个操作，就是某一段的奶牛要离开。然后要对区间进行这些操作，线段树是最好不过的了，这棵树要返回什么值，维护什么值呢？首先我们可以思考判断这棵树能不能存在可以住的房间，那就是询问这个区间的最大的连续的空房子的长度，看他有没有大于当前奶牛要住的区间。如果大的话就左儿子，右儿子，自己分别递归找到一个可以放下的位置，（优先左儿子，自己再到右儿子）。可是一般的线段树是(seg[root]=max(seg[lson],seg[rson]);)这样的，但是这一棵线段树有一点小特殊，因为如图

 

他可能是这样存在的（0表示空房子1表示有人住），LSON的最大值是3RLSON的最大值也是3，但是这一段的最大值是4,（LSON的右边两个加上RSON左边两个），所以我们还要维护两个量，从左边开始最长的空房间和右边开始的最长空房间，在push_up的时候，最大值就有三种取法，左儿子，右儿子，两个中间拼在一起。同时区间的左边最长，和右边最长也要更新。然后就是这样子不断维护它，询问最大值就完成了。

H - Help with Intervals

    其实这道题目的要点是读懂集合之间的运算，规则，用这种规则，对线段树中的每一个下表进行操作，然后就没有什么很难的地方了，注意：开闭区间是一个坑。

题目如下

A - I Hate It

 很多学校流行一种比较的习惯。老师们很喜欢询问，从某某到某某当中，分数最高的是多少。 
这让很多学生很反感。 

不管你喜不喜欢，现在需要你做的是，就是按照老师的要求，写一个程序，模拟老师的询问。当然，老师有时候需要更新某位同学的成绩。

Input

本题目包含多组测试，请处理到文件结束。 
在每个测试的第一行，有两个正整数 N 和 M ( 0，分别代表学生的数目和操作的数目。 
学生ID编号分别从1编到N。 
第二行包含N个整数，代表这N个学生的初始成绩，其中第i个数代表ID为i的学生的成绩。 
接下来有M行。每一行有一个字符 C (只取'Q'或'U') ，和两个正整数A，B。 
当C为'Q'的时候，表示这是一条询问操作，它询问ID从A到B(包括A,B)的学生当中，成绩最高的是多少。 
当C为'U'的时候，表示这是一条更新操作，要求把ID为A的学生的成绩更改为B。 

Output

对于每一次询问操作，在一行里面输出最高成绩。

Sample Input

5 6

1 2 3 4 5

Q 1 5

U 3 6

Q 3 4

Q 4 5

U 2 9

Q 1 5

Sample Output

5

6

5

9

 

 

       

  

Hint

Huge input,the C function scanf() will work better than cin

B - A Simple Problem with Integers

 You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.

Output

You need to answer all Q commands in order. One answer in a line.

Sample Input

10 5

1 2 3 4 5 6 7 8 9 10

Q 4 4

Q 1 10

Q 2 4

C 3 6 3

Q 2 4

Sample Output

4

55

9

15

Hint

The sums may exceed the range of 32-bit integers.

C - Naive Operations

 In a galaxy far, far away, there are two integer sequence a and b of length n. 
b is a static permutation of 1 to n. Initially a is filled with zeroes. 
There are two kind of operations: 
1. add l r: add one for $a_l,a_{l+1}...a_r$ 
2. query l r: query $\sum_{i=l}^r \lfloor a_i / b_i \rfloor$

Input

There are multiple test cases, please read till the end of input file. 
For each test case, in the first line, two integers n,q, representing the length of a,b and the number of queries. 
In the second line, n integers separated by spaces, representing permutation b. 
In the following q lines, each line is either in the form 'add l r' or 'query l r', representing an operation. 
$1 \leq n,q \leq 100000$, $1 \leq l \leq r \leq n$, there're no more than 5 test cases. 

Output

Output the answer for each 'query', each one line. 

Sample Input

5 12

1 5 2 4 3

add 1 4

query 1 4

add 2 5

query 2 5

add 3 5

query 1 5

add 2 4

query 1 4

add 2 5

query 2 5

add 2 2

query 1 5

Sample Output

1

1

2

4

4

6

D - 约会安排

 　　寒假来了，又到了小明和女神们约会的季节。 
　　小明虽为屌丝级码农，但非常活跃，女神们常常在小明网上的大段发言后热情回复“呵呵”，所以，小明的最爱就是和女神们约会。与此同时，也有很多基友找他开黑，由于数量实在过于巨大，怎么安排时间便成了小明的一大心事。 
　　我们已知小明一共有T的空闲时间，期间会有很多女神或者基友来找小明。 
　　作为一个操作系统曾经怒考71分的大神，小明想到了一个算法，即“首次适应算法”，根据操作系统课本的描述，就是找一段最靠前的符合要求的连续空间分配给每个请求，由此小明做出了一个决定： 
　　当一个基友来找小明时，小明就根据“首次适应算法”来找一段空闲的时间来和基友约好，如果找到，就说“X,let’s fly”（此处，X为开始时间），否则就说“fly with yourself”；
　　当女神来找小明时，先使用一次“首次适应算法”，如果没有找到，小明就冒着木叽叽的风险无视所有屌丝基友的约定，再次使用“无视基友首次适应算法”，两次只要有一次找到，就说“X,don’t put my gezi”（此处，X为开始时间），否则就说“wait for me” 
　　当然，我们知道小明不是一个节操负无穷的人，如果和女神约会完，还有剩余时间，他还是会和原来约好的基友去dota的。（举个例子：小西（屌丝）和小明约好在1~5这个时间单位段内打dota，这时候，女神来和小明预约长度为3的时间段，那么最终就是1~3小明去和女神约会，搞定后在4~5和小西打dota） 
　　小明偶尔也会想要学习新知识，此时小明就会把某一个时间区间的所有已经预定的时间全部清空用来学习并且怒吼“I am the hope of chinese chengxuyuan!!”，不过小明一般都是三分钟热度，再有人来预定的话，小明就会按耐不住寂寞把学习新知识的时间分配出去。

Input

输入第一行为CASE，表示有CASE组测试数据； 
每组数据以两个整数T，N开始，T代表总共的时间，N表示预约请求的个数； 
接着的N行，每行表示一个女神或者基友的预约，“NS QT”代表一个女神来找小明约一段长为QT的时间，“DS QT”则代表一个屌丝的长为QT的请求，当然也有可能是小明想学知识了，“STUDY!! L R”代表清空L~R区间内的所有请求。 

[Technical Specification] 
1. 1 <= CASE <= 30 
2. 1 <= T, N <= 100000 
3. 1 <= QT <= 110000 
4. 1 <= L <= R <=T

Output

对于每一个case，第一行先输出“Case C:”代表是第几个case，然后N行，每行对应一个请求的结果(参照描述)。 
输出样本(可复制此处)： 
“X,let's fly”,”fly with yourself”,”X,don't put my gezi”,”wait for me”,”I am the hope of chinese chengxuyuan!!” 

Sample Input

1

5 6

DS 3

NS 2

NS 4

STUDY!! 1 5

DS 4

NS 2

Sample Output

Case 1:

1,let's fly

4,don't put my gezi

wait for me

I am the hope of chinese chengxuyuan!!

1,let's fly

1,don't put my gezi

E - Stars in Your Window

 Fleeting time does not blur my memory of you. Can it really be 4 years since I first saw you? I still remember, vividly, on the beautiful Zhuhai Campus, 4 years ago, from the moment I saw you smile, as you were walking out of the classroom and turned your head back, with the soft sunset glow shining on your rosy cheek, I knew, I knew that I was already drunk on you. Then, after several months’ observation and prying, your grace and your wisdom, your attitude to life and your aspiration for future were all strongly impressed on my memory. You were the glamorous and sunny girl whom I always dream of to share the rest of my life with. Alas, actually you were far beyond my wildest dreams and I had no idea about how to bridge that gulf between you and me. So I schemed nothing but to wait, to wait for an appropriate opportunity. Till now — the arrival of graduation, I realize I am such an idiot that one should create the opportunity and seize it instead of just waiting. 

These days, having parted with friends, roommates and classmates one after another, I still cannot believe the fact that after waving hands, these familiar faces will soon vanish from our life and become no more than a memory. I will move out from school tomorrow. And you are planning to fly far far away, to pursue your future and fulfill your dreams. Perhaps we will not meet each other any more if without fate and luck. So tonight, I was wandering around your dormitory building hoping to meet you there by chance. But contradictorily, your appearance must quicken my heartbeat and my clumsy tongue might be not able to belch out a word. I cannot remember how many times I have passed your dormitory building both in Zhuhai and Guangzhou, and each time aspired to see you appear in the balcony or your silhouette that cast on the window. I cannot remember how many times this idea comes to my mind: call her out to have dinner or at least a conversation. But each time, thinking of your excellence and my commonness, the predominance of timidity over courage drove me leave silently. 

Graduation, means the end of life in university, the end of these glorious, romantic years. Your lovely smile which is my original incentive to work hard and this unrequited love will be both sealed as a memory in the deep of my heart and my mind. Graduation, also means a start of new life, a footprint on the way to bright prospect. I truly hope you will be happy everyday abroad and everything goes well. Meanwhile, I will try to get out from puerility and become more sophisticated. To pursue my own love and happiness here in reality will be my ideal I never desert. 

Farewell, my princess! 

If someday, somewhere, we have a chance to gather, even as gray-haired man and woman, at that time, I hope we can be good friends to share this memory proudly to relight the youthful and joyful emotions. If this chance never comes, I wish I were the stars in the sky and twinkling in your window, to bless you far away, as friends, to accompany you every night, sharing the sweet dreams or going through the nightmares together. 

Here comes the problem: Assume the sky is a flat plane. All the stars lie on it with a location (x, y). for each star, there is a grade ranging from 1 to 100, representing its brightness, where 100 is the brightest and 1 is the weakest. The window is a rectangle whose edges are parallel to the x-axis or y-axis. Your task is to tell where I should put the window in order to maximize the sum of the brightness of the stars within the window. Note, the stars which are right on the edge of the window does not count. The window can be translated but rotation is not allowed. 

Input

There are several test cases in the input. The first line of each case contains 3 integers: n, W, H, indicating the number of stars, the horizontal length and the vertical height of the rectangle-shaped window. Then n lines follow, with 3 integers each: x, y, c, telling the location (x, y) and the brightness of each star. No two stars are on the same point. 

There are at least 1 and at most 10000 stars in the sky. 1<=W，H<=1000000, 0<=x，y<2^31. 

Output

For each test case, output the maximum brightness in a single line.

Sample Input

3 5 4

1 2 3

2 3 2

6 3 1

3 5 4

1 2 3

2 3 2

5 3 1

Sample Output

5

6

F - Mayor's posters

 The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
• The wall is divided into segments and the width of each segment is one byte. 
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l i, l i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

The picture below illustrates the case of the sample input.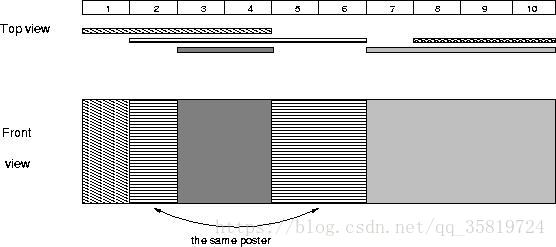 

Sample Input

1

5

1 4

2 6

8 10

3 4

7 10

Sample Output

4

G - Hotel

 The cows are journeying north to Thunder Bay in Canada to gain cultural enrichment and enjoy a vacation on the sunny shores of Lake Superior. Bessie, ever the competent travel agent, has named the Bullmoose Hotel on famed Cumberland Street as their vacation residence. This immense hotel has N (1 ≤ N ≤ 50,000) rooms all located on the same side of an extremely long hallway (all the better to see the lake, of course).

The cows and other visitors arrive in groups of size Di (1 ≤ Di ≤ N) and approach the front desk to check in. Each group i requests a set of Di contiguous rooms from Canmuu, the moose staffing the counter. He assigns them some set of consecutive room numbers r..r+Di-1 if they are available or, if no contiguous set of rooms is available, politely suggests alternate lodging. Canmuu always chooses the value of rto be the smallest possible.

Visitors also depart the hotel from groups of contiguous rooms. Checkout i has the parameters Xi and Di which specify the vacating of rooms Xi ..Xi +Di-1 (1 ≤ Xi ≤ N-Di+1). Some (or all) of those rooms might be empty before the checkout.

Your job is to assist Canmuu by processing M (1 ≤ M < 50,000) checkin/checkout requests. The hotel is initially unoccupied.

Input

* Line 1: Two space-separated integers: N and M
* Lines 2..M+1: Line i+1 contains request expressed as one of two possible formats: (a) Two space separated integers representing a check-in request: 1 and Di (b) Three space-separated integers representing a check-out: 2, Xi, and Di

Output

* Lines 1.....: For each check-in request, output a single line with a single integer r, the first room in the contiguous sequence of rooms to be occupied. If the request cannot be satisfied, output 0.

Sample Input

10 6

1 3

1 3

1 3

1 3

2 5 5

1 6

Sample Output

1

4

7

0

5

H - Help with Intervals

 LogLoader, Inc. is a company specialized in providing products for analyzing logs. While Ikki is working on graduation design, he is also engaged in an internship at LogLoader. Among his tasks, one is to write a module for manipulating time intervals, which have confused him a lot. Now he badly needs your help.

In discrete mathematics, you have studied several basic set operations, namely union, intersection, relative complementation and symmetric difference, which naturally apply to the specialization of sets as intervals.. For your quick reference they are summarized in the table below:

Operation	Notation	Definition
Union	A ∪ B	{x : x ∈ A or x ∈ B}
Intersection	A ∩ B	{x : x ∈ A and x ∈ B}
Relative complementation	A − B	{x : x ∈ A but B}
Symmetric difference	A ⊕ B	(A − B) ∪ (B − A)

Ikki has abstracted the interval operations emerging from his job as a tiny programming language. He wants you to implement an interpreter for him. The language maintains a set S, which starts out empty and is modified as specified by the following commands:

Command	Semantics
U T	S ← S ∪ T
I T	S ← S ∩ T
D T	S ← S − T
C T	S ← T − S
S T	S ← S ⊕ T

Input

The input contains exactly one test case, which consists of between 0 and 65,535 (inclusive) commands of the language. Each command occupies a single line and appears like

X T

where X is one of ‘U’, ‘I’, ‘D’, ‘C’ and ‘S’ and T is an interval in one of the forms (a,b), (a,b], [a,b) and [a,b] (a, b ∈ Z, 0 ≤ a ≤ b ≤ 65,535), which take their usual meanings. The commands are executed in the order they appear in the input.

End of file (EOF) indicates the end of input.

Output

Output the set S as it is after the last command is executed as the union of a minimal collection of disjoint intervals. The intervals should be printed on one line separated by single spaces and appear in increasing order of their endpoints. If S is empty, just print “empty set” and nothing else.

Sample Input

U [1,5]

D [3,3]

S [2,4]

C (1,5)

I (2,3]

Sample Output

(2,3)