蓝桥杯：人物相关性分析

蓝桥杯：人物相关性分析https://www.lanqiao.cn/problems/198/learning/

目录

题目描述   

输入描述

输出描述

输入输出样例

输入

输出

输入

输出

运行限制

题目分析:(滑动窗口)

AC代码（JAVA）

---

题目描述   

        小明正在分析一本小说中的人物相关性。他想知道在小说中 Alice 和 Bob 有多少次同时出现。

        更准确的说，小明定义 Alice 和 Bob "同时出现" 的意思是：在小说文本 中 Alice 和 Bob 之间不超过 K 个字符。

        例如以下文本：

This is a story about Alice and Bob.Alice wants to send a private message to Bob.

        假设 K = 20，则 Alice 和 Bob 同时出现了 2 次，分别是"Alice and Bob" 和 "Bob. Alice"。前者 Alice 和 Bob 之间有 5 个字符，后者有 2 个字符。

注意:

1. Alice 和 Bob 是大小写敏感的，alice 或 bob 等并不计算在内。

2. Alice 和 Bob 应为单独的单词，前后可以有标点符号和空格，但是不能 有字母。例如出现了 Bobbi 并不算出现了 Bob。

输入描述

        第一行包含一个整数 K（1≤K≤）。

        第二行包含一行字符串，只包含大小写字母、标点符号和空格。长度不超过 。

输出描述

输出一个整数，表示 Alice 和 Bob 同时出现的次数。

输入输出样例

输入

20
This is a story about Alice and Bob.Alice wants to send a private message to Bob.

输出

2

输入

1000
Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Alice.Bob.Bob.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Alice.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Bob.Bob.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Bob.Alice.Bob.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Bob.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Bob.Alice.Alice.Alice.Alice.Bob.Bob.Bob.Bob.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Bob.Bob.Alice.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Bob.Alice.Alice.Bob.Alice.Alice.

输出

191784

运行限制

• 最大运行时间：1s
• 最大运行内存: 512M

题目分析:(滑动窗口)

        我们需要记录下每个Alice和Bob出现的下标，记录Alice和Bob这两个单词首字母出现的下标，方便后续进行操作，不然每次搜索Alice的时候都需要进行equals判断，耗时非常高的。

        遍历给定字符串str，我们分别记录下Alice和Bob出现的下标，分别存储到两个数组中，并且记录长度。

        判断出现的下标的时候，首先判断头部是A还是B，如果是A，那么就需要判断末尾是否位e，则判断后面第四位是不是e。

        B同理，同样需要判断末尾是不是b，也就是判断判断后面第二位是不是b。

        如果是了，就在进行字符串截取和比较，与Alice or Bob相同则记录到数组中。

        //记录Alice和Bob出现的下标
        for(int i = 0;i

             如果使用双重for循环来遍历Alice和Bob数组的话，肯定会有超时的，但也能拿80%。

        所以我们要对双重for进行优化，我们这里选择滑动窗口进行优化，下面是可行性分析：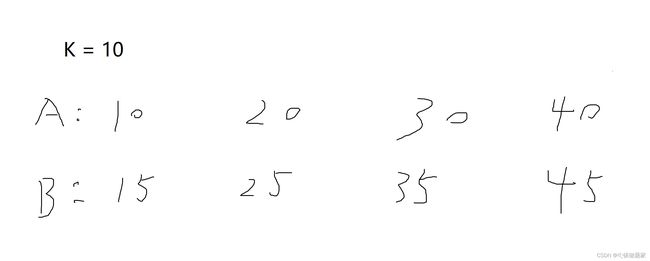        

        如同所示，假设K=10，A，B数组存放Alice和Bob出现的下标，如图所示。

        那么，我们看一下哪个范围可以使A[0] = 10,与B[i]相差不超过10，

        [ A[0] - 10, A[0] + 10 ] 也就是说，如果处于这个范围之内，Alice和Bob是合法的。

        但是题目中是有限制的：

        如 "Alice and Bob" 之间有5个字符。

        如"Bob.Alice"之间有1个字符。

        也就是说，如果从Alice，往右边数的话，其实是要从Alice的e，到K个字符之间，都算合法距离。也就是说，Alice记录的是A出现的下标，但是从Alice往右边数是从e开始数的，所以实际计算记录应该要+4。

        同样，假如Bob在Alice左边，那么实际有效范围应该是从Bob的b到Alice的A，那么记录Bob出现的下标只记录了B，那么如果要从b开始，就要+上2，才算是Bob实际的出现次数。

        这里继续距离，当K=5，如果Alice[i] = 15，那么他的合法数据范围应该是 10-15,15-20。

        左边界10也就是Bob的b必须在的位置，右边界20必须是Bob的B所在的位置

         如此我们可以汇总得到范围为 [ Alice[i]-K-2,Alice[i]+K+4 ] 。

        也就是在[ Alice[i]-K-2,Alice[i]+K+4 ] 范围内的数据都是合法的，那么我们需要left和right，都在这个范围之外，这样就能保证right-left 就能得到这个区间内合法的数据

        也就是时刻要保证Bob[left] < Alice[i]-K-2, 并且 Alice[i]+K+4 < Bob[right].

        推导出公式，接下来是窗口的滑动问题，

        我们可以假设如果 Bob[left] == Alice[i]-k+2 并且 Alice[i]+k+4 == Bob[right]，

        那么Alice[i+1]必定大于Bob[left]+k+2,同时也大于Bob[right]+k+4，所以我们的窗口只需要跟着i进行滑动即可，也就是在第一次滑动之后每次根据Alice[i]的值进行滑动，避免重复计算，减少Bob数组的遍历。

AC代码（JAVA）

        代码中为了保证Bob[right] > Alice[i]+K+4,则每次当 Bob[right] < Alice[i]+K+5时，就让right右移。

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    static int K;
    static String str;
    public static void init() {
        Scanner scan = new Scanner(System.in);
        K = scan.nextInt();
        scan.nextLine();
        str = scan.nextLine();
        scan.close();
    }

    static int[] Alice = new int[1000000];
    static int length = 0;
    static int[] Bob = new int[1000000];
    static int size = 0;
    public static void main(String[] args) {
        init();
        int len = str.length();

        //记录Alice出现的下标
        for(int i = 0;i<=len-5;i++) {
            //判断首尾是否相同
            if(str.charAt(i) == 'A' && str.charAt(i+4) == 'e') {
                //在截取判断
                if(str.substring(i,i+5).equals("Alice")) Alice[length++] = i;
            }
        }
        //记录Bob出现的下标
        for(int i = 0;i<=len-3;i++) {
            //判断首尾是否相同
            if(str.charAt(i) == 'B' && str.charAt(i+2) == 'b') {
                //截取判断
                if(str.substring(i,i+3).equals("Bob")) Bob[size++] = i;
            }
        }

        //以Alice进行遍历，那么在他的范围内，就是[Alice[i]-k,Alice[i]+k]
        //但是如果Bob在Alice的左边，那么需要算上o和b这两个字符，所以左边界应该是[Alice[i]-k+2
        //如果Bob在Alice右边，那么是从Alice的e开始计算到Bob的计算，那么右边界就是[Alice[i]+k+4
        long ans = 0;
        //这里可以推导，假设Bob[left] == Alice[i]-k+2 && Alice[i]+k+4 == Bob[right]
        //那么Alice[i+1]必定大于Bob[left]+k+2,同时也大于Bob[right]+k+4
        //因此双指针定义在循环外面，作为窗口，跟着i进行滑动
        int left = 0;
        int right = 0;
        for(int i = 0;i Bob[left]) {
                left++;
            }
            //扩展右窗口,必须保证Bob[right]  > Alice[i]+K+4
            while(right < size && Alice[i]+K+5 > Bob[right]) {
                right++;
            }
            //当前位置的数量就是 右窗口-左窗口
            ans += Math.max((right-left),0);
        }

        System.out.println(ans);
    }
}