算法训练营 - 广度优先BFS
目录
从层序遍历开始
N 叉树的层序遍历
经典BFS最短路模板
经典C++ queue
数组模拟队列
打印路径
示例1.bfs查找所有连接方块
C++queue版
数组模拟队列
示例2.从多个位置同时开始BFS
示例3.抽象最短路类(作图关键)
示例4.跨过障碍的最短路
从层序遍历开始
广度优先搜索(Breadth First Search,BFS),又称为宽度优先搜索,是最常见的图搜索方法之一。广度优先搜索是从某个顶点(源点)出发,一次性访问所有未被访问的邻接点,再依次从这些访问过邻接点出发,…,似水中涟漪,似声音传播,一层层地传播开来。
广度优先遍历是按照广度优先搜索的方式对图进行遍历。
广度优先搜索模型
Bfs()
{
1. 建立起始步骤,队列初始化
2. 遍历队列中的每一种可能,whlie(队列不为空)
{
通过队头元素带出下一步的所有可能,并且依次入队
{
判断当前情况是否达成目标:按照目标要求处理逻辑
}
继续遍历队列中的剩余情况
}
}
(看不懂没有关系,直接看题就完事儿了)
N 叉树的层序遍历
力扣
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector> levelOrder(Node* root) {
vector v;
vector> vec;
queue q;
if(!root) return vec;
q.push(root);//将开始bfs位置入队
while(!q.empty())
{
int n=q.size();//需要遍历这一层的元素个数
for(int i=0;ival);
//将这个点所连接的点入队
vector son=temp->children;
for(int j=0;j 经典BFS最短路模板
经典C++ queue
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
int n, m;
int g[N][N], d[N][N];
int bfs()
{
queue< pair > q;
q.push({0, 0});
memset(d, -1, sizeof(d));
d[0][0] = 0;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (q.size())//队列不为空
{
PII t = q.front();//取队头元素
q.pop();//出队
for (int i = 0; i < 4; i++)
{
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;//当前点到起点的距离
q.push({x, y});//将新坐标入队
}
}
}
return d[n - 1][m -1];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
数组模拟队列
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
PII q[N * N];//手写队列
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过
d[0][0] = 0;//表示起点走过了
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左
while(hh <= tt)//队列不空
{
PII t = q[hh ++ ];//取队头元素
for(int i = 0; i < 4; i ++ )//枚举4个方向
{
int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过
{
d[x][y] = d[t.first][t.second] + 1;//到起点的距离
q[ ++ tt ] = {x, y};//新坐标入队
}
}
}
return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
打印路径
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
PII q[N*N],Prev[N][N];
int g[N][N], d[N][N];
int n, m;
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, -1, sizeof d);
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
d[0][0] = 0;
while(hh <= tt)
{
PII t = q[hh ++ ];
for(int i = 0; i < 4; i ++ )
{
int x = dx[i] + t.first, y = t.second + dy[i];
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;
Prev[x][y] = t;
q[++ tt] = {x, y};
}
}
}
int x = n - 1, y = m - 1;
while(x || y)//有一个不d等于0
{
cout << x << ' ' << y << endl;
PII t = Prev[x][y];
x = t.first, y = t.second;
}
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m;j ++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
输入
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出
4 4
3 4
2 4
2 3
2 2
2 1
2 0
1 0
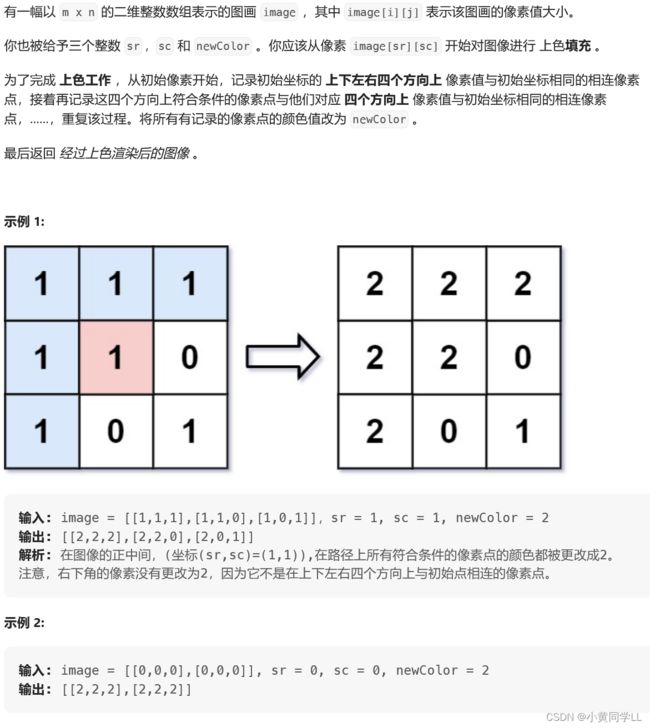
8示例1.bfs查找所有连接方块
力扣
思路:
非常简单,就是把图块的四个方向都搜索一遍,对于每个相邻的同色图块修改成新色即可
C++queue版
class Solution {
public:
const int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
vector> floodFill(vector>& image, int sr, int sc, int color) {
int old=image[sr][sc];
if(old==color) return image;
int n=image.size(),m=image[0].size();
queue> q;
q.push({sr,sc});
image[sr][sc]=color;
while(!q.empty())
{
pair t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if(x>=0&&x=0&&y 数组模拟队列
class Solution {
public:
const int dx[4] = {1, 0, 0, -1},dy[4] = {0, 1, -1, 0};
vector> floodFill(vector>& image, int sr, int sc, int color) {
int old = image[sr][sc];
if (old == color) return image;
int n = image.size(), m = image[0].size();
int hh=0,tt=0;
pair q[n*m];
q[0]={sr,sc};
image[sr][sc] = color;
while (hh<=tt) {
pair t=q[hh++];
for (int i = 0; i < 4; i++) {
int x = t.first+dx[i], y = t.second+dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && image[x][y] == old) {
q[++tt]={x,y};
image[x][y] = color;
}
}
}
return image;
}
};
示例2.从多个位置同时开始BFS
力扣
本题可以先找到所有的腐烂橘子,入队,用第一批带出新一批腐烂的橘子
每以匹橘子都会在一分钟之内腐烂,所以此题可以转化为求BFS执行的大循环的次数
这里的step的更新需要有一个标记,只有新的腐烂的橘子加入,step才能自加
最后BFS执行完之后,说明所有可以被腐烂的都完成了,再去遍历grid,如何还有
值为1的,说明没有办法完全腐烂,返回-1,如果没有,则返回step
class Solution {
public:
int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
int orangesRotting(vector>& grid) {
int n=grid.size(),m=grid[0].size();
queue> q;
int cnt=0;
int step=0;
for(int i=0;i t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if(x>=0&&x=0&&y 示例3.抽象最短路类(作图关键)
力扣
思路:
- 通过BFS, 首先用beginWord带出转换一个字母之后所有可能的结果
- 每一步都要把队列中上一步添加的所有单词转换一遍,最短的转换肯定在这些单词当中, 所有这些词的转换只能算一次转换,因为都是上一步转换出来的,这里对于每个单词的每个位置都可以用26个字母进行转换,所以一个单词一次转换的可能有:单词的长度 * 26
- 把转换成功的新词入队,进行下一步的转换
- 最后整个转换的长度就和BFS执行的次数相同
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector& wordList) {
//hash表的查询效率最高,将单词存入哈希表
unordered_set wordDict(wordList.begin(), wordList.end());
//标记单词是否已经访问过,访问过的不再访问
unordered_set visited;
visited.insert(beginWord);
//初始化队列
queue q;
q.push(beginWord);
int res = 1;
while (!q.empty())
{
int nextSize = q.size();
while (nextSize--)
{
string curWord = q.front();
q.pop();
if (curWord == endWord)
return res ;
//尝试转换当前单词的每一个位置
for (int i = 0; i < curWord.size(); i++)
{
string newWord = curWord;
//每一个位置用26个字母分别替换
for (char ch = 'a'; ch <= 'z'; ch++)
{
newWord[i] = ch;
//在字典里且没有用过
if (wordDict.count(newWord) && !visited.count(newWord))
{
visited.insert(newWord);//标记用过
q.push(newWord);
}
}
}
}
res++;
}
//转换不成功,返回0
return 0;
}
}; 示例4.跨过障碍的最短路
力扣
障碍指不可到达的路径,这种障碍一般用数组或者hash表存储,用if判断此路不通;
思路:
深度优先不适合解此题,递归深度太大,会导致栈溢出
本题的密码为4位密码,每位密码可以通过拨动一次进行改变,注意这里的数的回环以及拨动的方向
拨动方向:向前,向后
回环:如果当前是9,0时,向前,向后拨动需要变成最小最大,而不是简单的自加自减
class Solution {
public:
int openLock(vector& deadends, string target) {
// 哈希表的查找更快
unordered_set deadendsSet(deadends.begin(), deadends.end());
//如果"0000"在死亡字符串中,则永远到达不了
if (deadendsSet.find("0000") != deadendsSet.end())
return -1;
//初始化队列
queue que;
que.push("0000");
//加标记,已经搜索过的字符串不需要再次搜索
unordered_set book;
book.insert("0000");
int step = 0;
while (!que.empty()) {
int n = que.size();
//从上一步转换之后的字符串都需要进行验证和转换
//并且只算做一次转换,类似于层序遍历,转换的步数和层相同
//同一层的元素都是经过一步转换得到的
while(n--)
{
string curStr = que.front();
que.pop();
if (curStr == target) return step;
//四位密码锁,每个位置每次都可以转一次
for (int j = 0; j < 4; j++)
{
string newStr1 = curStr, newStr2 = curStr;
//当前位置可以向前或者向后拨一位
newStr1[j] = newStr1[j] == '9' ? '0' : newStr1[j] + 1;
newStr2[j] = newStr2[j] == '0' ? '9' : newStr2[j] - 1;
//如果不会死锁且没有尝试过,则入队
if (deadendsSet.find(newStr1) == deadendsSet.end()
&& book.find(newStr1) == book.end()) {
que.push(newStr1);
book.insert(newStr1);
}
if (deadendsSet.find(newStr2) == deadendsSet.end()
&& book.find(newStr2) == book.end()) {
que.push(newStr2);
book.insert(newStr2);
}
}
}
step++;
}
return -1;
}
};