【CUDA】yolov5前处理

1. 仿射变换

1.1 旋转

变换公式：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\text{\hspace{1em}(1.1)}$$
具体推导

由于opencv的图像坐标原点在左上角，y轴向下，因此变换矩阵为：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\text{\hspace{1em}(1.2)}$$

1.2 缩放

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\text{scale}& 0\\ 0& \text{scale}\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\text{\hspace{1em}(1.3)}$$

1.3 缩放加旋转

$$\left[\begin{array}{cc}\text{scale}& 0\\ 0& \text{scale}\end{array}\right]\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]=\left[\begin{array}{cc}\cos \theta \times \text{scale}& \sin \theta \times \text{scale}\\ -\sin \theta \times \text{scale}& \cos \theta \times \text{scale}\end{array}\right]\text{\hspace{1em}(1.4)}$$

1.4 平移变换

[ x ′ y ′ 1 ] = [ 1 0 d x 0 1 d y 0 0 1 ] [ x y 1 ] (1.5) \begin{bmatrix} x'\\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \\ 1 \end{bmatrix} \tag{1.5} ​x′y′1​ ​= ​100​010​dxdy1​ ​ ​xy1​ ​(1.5)

1.5 统一使用齐次坐标表示仿射变换(旋转、缩放、平移等)

[ x ′ y ′ 1 ] = [ s cos ⁡ θ s sin ⁡ θ d x − s sin ⁡ θ s cos ⁡ θ d y 0 0 1 ] [ x y 1 ] (1.6) \begin{bmatrix} x'\\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s\cos \theta & s\sin \theta & dx\\ -s\sin \theta & s\cos \theta & dy\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \\ 1 \end{bmatrix} \tag{1.6} ​x′y′1​ ​= ​scosθ−ssinθ0​ssinθscosθ0​dxdy1​ ​ ​xy1​ ​(1.6)

1.6 仿射变换逆变换

仿射变换的逆变换是指，将变换(旋转、平移、缩放)过后的图片变换回原图的操作。正向的仿射变换：
$$x^{\prime }=Mx\text{\hspace{1em}(1.7)}$$
仿射变换的逆变换：
$$x=M^{-1}{x}^{\prime }\text{\hspace{1em}(1.8)}$$

2. yolov5 预处理 python实现

2.1 yolov5预处理

对于目标检测推理而言，通常需要图像等比例缩放并且居中

可以分解为三个仿射变换：

2.1.1 缩放

缩放比例 $\text{scale}$ 为：
$$\text{scale}=\min (\frac{dstW}{oriW},\frac{dstH}{oriH})\text{\hspace{1em}(2.1)}$$
缩放后的图像尺寸为：
$$\begin{array}{rlr}imgW=& dstW-\text{scale}\times oriWimgH=& dstH-\text{scale}\times oriH\end{array}\text{\hspace{1em}(2.2)}$$

2.1.2 平移

平移矩阵为：
t r a n s M = [ 1 0 − scale × o r i W / 2 0 1 − scale × o r i H / 2 0 0 1 ] (2.2) transM = \begin{bmatrix}1 & 0 &- \text{scale} \times oriW /2\\ 0 &1 & - \text{scale} \times oriH/2 \\ 0 & 0 & 1 \text{} \end{bmatrix} \tag{2.2} transM= ​100​010​−scale×oriW/2−scale×oriH/21​ ​(2.2)

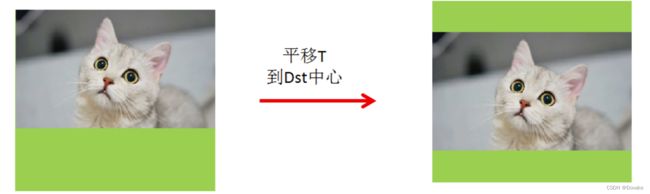
2.1.3 将图像中心平移至画布中心

变换矩阵：
t r a n s M 1 = [ 1 0 d s t W / 2 0 1 d s t H / 2 0 0 1 ] (2.3) transM1 = \begin{bmatrix}1 & 0 & dstW /2\\ 0 &1 & dstH/2 \\ 0 & 0 & 1 \text{} \end{bmatrix} \tag{2.3} transM1= ​100​010​dstW/2dstH/21​ ​(2.3)

这三步分解，其实是为了方便分析复杂的仿射变换组合。因为仿射变换是矩阵乘法是具有可叠加性的。

我们可以得到最后的仿射变换矩阵：
$$\begin{array}{rl}tw=& -\text{scale}\times oriW/2+dstW/2\\ th=& -\text{scale}\times oriH/2+dstH/2\end{array}\text{\hspace{1em}(2.4)}$$

M = [ scale 0 t w 0 scale t h 0 0 1 ] (2.4) M = \begin{bmatrix}\text{scale} & 0 & tw \\ 0 &\text{scale} & th\\ 0 & 0 & 1 \text{} \end{bmatrix} \tag{2.4} M= ​scale00​0scale0​twth1​ ​(2.4)

逆变换：
M = [ 1 / scale 0 − t w scale 0 1 / scale − t h scale 0 0 1 ] (2.5) M = \begin{bmatrix} 1/\text{scale} & 0 & -\frac{tw }{\text{scale}} \\ \\ 0 & 1/ \text{scale} & -\frac{th }{\text{scale}} \\ \\ 0 & 0 & 1 \text{} \end{bmatrix} \tag{2.5} M= ​1/scale00​01/scale0​−scaletw​−scaleth​1​ ​(2.5)

2.2 双线性插值

2.2.1 双线性插值原理

2.2.1 双线性插值python实现

python代码

def pyWarpAffine(image, M, dst_size, constant=(0,0,0)):
	'''
		@brief: 带双线性插值的仿射变换，目的像素由源图中的相邻四个点的像素加权决定。
				由目的像素位置，计算源图中的对应位置点，并求出原图中相邻四个点的像素值
				将原图中的四个点加权得到目的图像素的像素值
				如果目的图像素找不到，则使用constant的值代替
		@param image(np.ndarray) 	原图
		@param M(np.ndarray) 		变换矩阵
		@param dst_size(tuple)		目标图的尺寸
		@param constant(tuple) 		当找不到像素是，使用constat代替
	'''
	# 取逆矩阵， dst --> src 变换的矩阵
	M = cv2.invertAffineTransform(M)
	constant = np.array(constant)
	ih, iw = image.shape[:2]
	dw, dh = dst_size
	dst = np.full((dh, dw, 3), constant, dtype=np.uint8)
	in_range = lambda p : p[0] >=0 and p[0] <= dw and p[1] >= 0 and p[1] <= dh
	for y in range(dh):
		for x in range(dw):
			homo_coord = np.array([[x, y, 1]]).T
			ox, oy = M @ homo_coord

			low_ox = int(np.floor(ox))
			low_oy = int(np.floor(oy))
			high_ox = low_ox + 1
			high_oy = low_oy + 1
			# |(low_ox,  low_oy) .........(high_ox, low_oy)
			# |........p0...............|........p1........|
			# |-------------------------|o(dx, dy)---------|
			# |.........................|..................|
			# |........p2...............|........p3........|
			# |.........................|..................|
			# | (low_ox, high_oy) .......(high_ox, high_oy)|
			
			dx, dy = ox - low_ox, oy - low_oy
			# 取对角矩形的面积作为自己的权重
			p0_wight = (1-dx)* (1-dy)
			p1_wight = dx * (1-dy)
			p2_wight = (1-dx) * dy
			p3_wight = dx * dy
			p0_value = image[(low_ox, low_oy)] if in_range((low_ox, low_oy) else constant)
			p1_value = image[(high_ox, low_oy)] if in_range((high_ox, low_oy) else constant)
			p2_value = image[(low_ox, high_ox)] if in_range((low_ox, high_ox) else constant)
			p3_value = image[(high_ox, high_ox)] if in_range((high_ox, high_ox) else constant)
			dst[y, x] = p0_wight * p0_value + p1_wight * p1_value + p2_wight * p2_value + p3_wight * p3_value
	return dst

3. yolov5 预处理 cuda实现

3.1 仿射变换

__device__ void affine_project(float* matrix, int x, int y, float* proj_x, float* proj_y) {
    *proj_x = matrix[0] * x + matrix[1] * y + matrix[2];
    *proj_y = matrix[3] * x + matrix[4] * y + matrix[5];
}

__global__ void warp_affine_bilinear_kernel (
    uint8_t* src, int src_width, int src_height,
    uint8_t* dst, int dst_width, int dst_height,
    uint8_t  fill_val, AffineMatrix matrix,
    int channels = 3, bool brg2rgb = true
) {

    int src_line_size   = src_height * channels;
    int dst_line_size   = dst_height * channels;

    int dx = blockDim.x * blockIdx.x + threadIdx.x;
    int dy = blockDim.y * blockIdx.y + threadIdx.y;
    if ( dx >= dst_width || dy >= dst_height) return;

    float src_x = 0, src_y = 0;
    affine_project(matrix.d2i, dx, dy, &src_x, &src_y);

    float ch0 = fill_val, ch1 = fill_val, ch2 = fill_val;
    float *ch_data = new float[channels];
    for(int i = 0; i < channels; ++i) {
        ch_data[i] = fill_val;
    }

    if ( src_x >=0 && src_x <src_width && src_y >= 0 && src_y < src_height) {
        int low_x = floorf(src_x);
        int low_y = floorf(src_y);

        int high_x = low_x + 1;
        int high_y = low_y + 1;
        uint8_t* const_vals = new uint8_t[channels];
        for(int i = 0; i < channels; ++i) {
            const_vals[i] = fill_val;
        }

        // |(low_ox,  low_oy) .......|.(high_ox, low_oy)......|
        // |........p0...............|........p1..............|
        // |-------------------------|o(src_x, src_y)---------|
        // |.........................|........................|
        // |........p2...............|........p3..............|
        // |.........................|........................|
        // | (low_ox, high_oy) ......|(high_ox, high_oy)......|
        float dx = src_x - low_x;
        float dy = src_y - low_y;
        float p0_wt = (1-dx) * (1-dy);
        float p1_wt = dx * (1-dy);
        float p2_wt = (1-dx) * dy;
        float p3_wt = dx * dy;
        uint8_t* v0 = const_vals;
        uint8_t* v1 = const_vals;
        uint8_t* v2 = const_vals;
        uint8_t* v3 = const_vals;
        if (low_y >= 0) {
            if (low_x >= 0) {
                v0 = src + low_y * src_line_size + low_x * channels;
            }

            if (high_x < src_width) {
                v1 = src + low_y * src_line_size + high_x * channels;
            }
        }

        if(high_y < src_height) {
            if (low_x >= 0) {
                v2 = src + high_y * src_line_size + low_x * 3;
            }

            if (high_x < src_width) {
                v3 = src + high_y * src_line_size + high_x * 3;
            }
        }

        for (int i = 0; i < channels; ++i) {
            ch_data[i] = floorf(p0_wt * v0[i] + p1_wt * v1[i] + p2_wt * v2[i] + p3_wt * v3[i] + 0.5f);
        }

    } // end if

    uint8_t* pdst = dst + dy * dst_line_size + dx * channels;
    if (brg2rgb) {
        pdst[0] = ch_data[2];
        pdst[1] = ch_data[1];
        pdst[2] = ch_data[0];
        return;
    }

    for (int i = 0; i < channels; ++i) {
        pdst[i] = ch_data[i];
    }
}