动态规划学习整理

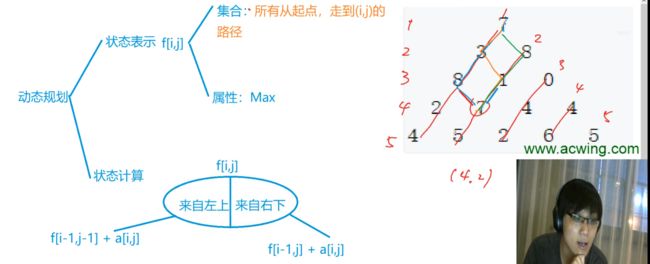
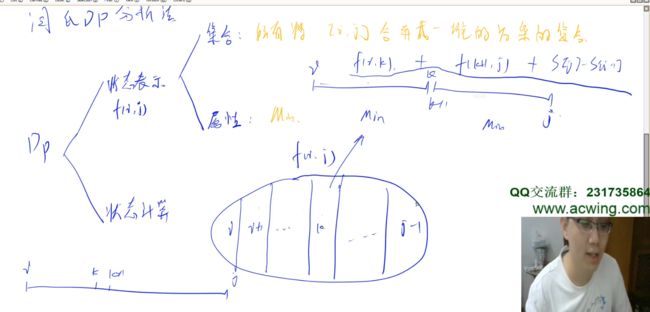
闫氏dp分析法

dp问题两步走：「状态定义」 和 「状态计算」

动态规划就是一个**「化零为整、化整为零」**的过程

状态定义

状态定义就是「化零为整」，用一个值（属性）将一个集合代表。

状态计算

状态计算就是「化整为零」，将一个大整体划分为一个个小问题求解。

状态计算基本要求

• 不重复（求最大最小值无所谓，求个数的的话需要满足）
• 不漏（无论如何都一定要满足）

状态计算划分依据比较

状态计算 化整为零的时候，一般都是找最后一个不同点来进行分割

• 背包问题：看最后一个物品怎么选的，按不同选法分类（选/不选/选几个）
• 最长上升子序列：看倒数第二个数大小分类
• 编辑距离：看两个字符串的最后一个字母是否相同分类
• 最长公共子序列：看最后两个字母的情况分类
  • 第一个字符串的最后一个字母包不包含在这个子序列中
  • 第二个字符串的最后一个字母包不包含在这个子序列中
  • 与上升子序列不同，子序列规定了必须包含最后一个字母，而这里没有
    • 在分析f(i-1,j)和f(i,j-1)的时候会有重复；这里无所谓，因为求得是max不是cnt
• 数字三角形：最后一步是怎么走下来

背包问题

01背包「用一次」

必然需要两重循环填充

但可以优化空间，二维数组->一维数组

根据状态计算公式，我们需要上一行靠前的数据，因此内层循环(单行)从后往前遍历。

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 1010;
    static int[] dp = new int[N];
    static int n,v;
    
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] arr = br.readLine().split(" ");
        n = Integer.parseInt(arr[0]);
        v = Integer.parseInt(arr[1]);
        for(int i=1;i<=n;i++){
            String[] arr1 = br.readLine().split(" ");
            int volume = Integer.parseInt(arr1[0]);
            int w = Integer.parseInt(arr1[1]);
            for(int j=v;j>=0;j--){
                if(volume<=j)dp[j]=Math.max(dp[j],dp[j-volume]+w);
            }
        }
        System.out.println(dp[v]);
    }
}

练习题单

• 416. 分割等和子集
• 1049. 最后一块石头的重量 II
• 474. 一和零
• 494. 目标和

完全背包「用无限次」

状态定义是与01背包一致。

两种理解方式完全背包的方式：

公式推导

因为可以用无限次，限制条件就变成了背包容量。

状态计算中，从01背包的 「选/不选」 过渡到了 选1次到选 「容量/当前物品的重量」 次

通过公式推导不难发现，在

dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-v]+w,dp[i-1][j-2v]+2w....,dp[i-1][0]+j/v*w)

而dp[i][j-v]=Math.max(dp[i-1][j-v],dp[i-1][j-2v]+w,dp[i-1][j-3v]+2w....,dp[i-1][0]+(j/v-1)*w)

在朴素做法中，公式后半段需要遍历求最大值的max其实就是dp[i][j-v]+w，因此我们可以把公式优化成

dp[i][j]=Math.max(dp[i-1][j],dp[i][j-v])，同时在进行空间一维优化的时候，因为dp[i][j-v]用到的是当前层处理好的数据，所以从前向后遍历，和01背包的一维从后向前遍历的本质不同原因也在此。

其他思路

通过之前推导公式我们不难看出，在遍历同一个物品的时候，完全背包代表着我们可以选多次。

因此我们当前层之前新更新的数据也可以被“复用”，即选一个物品可以基于其之前已经选过的结果来进行计算。变相选无限次。

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 1010;
    static int[] dp = new int[N];
    
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] arr = br.readLine().split(" ");
        int n = Integer.parseInt(arr[0]);
        int v = Integer.parseInt(arr[1]);
        for(int i=1;i<=n;i++){
            String[] arr1= br.readLine().split(" ");
            int volume = Integer.parseInt(arr1[0]);
            int w  = Integer.parseInt(arr1[1]);
            for(int j=0;j<=v;j++){
                if(j>=volume)dp[j]=Math.max(dp[j],dp[j-volume]+w);
            }
        }
        System.out.println(dp[v]);
        
    }
}

另附推导图：

练习题单

• 322. 零钱兑换

• 518. 零钱兑换 II

• 377. 组合总和 Ⅳ

• 70. 爬楼梯

• 279. 完全平方数

• 139. 单词拆分

多重背包「用K次」

暴力一点：把1个物品用K次，拆成K个相同重量和占用的物品用/不用，转换为01背包去做。

优化一点：

因为一个整数K可以拆分为二进制表示，我们只需要把原来K个物品拆分成二进制底数的组，再通过对这些组用/不用，代表选K次，从而将暴力的O(N)降为O(logN)

重点介绍多重背包的二进制优化

参考代码：

import java.util.*;
import java.io.*;

public class Main{
   static final int S = 2010,V=2010;
   static int[] dp = new int[V];
   static int[] w = new int[S*1000];
   static int[] v = new int[S*1000];
   static int n,idx;
   
   public static void main(String[] args)throws Exception{
       BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
       String[] arr = br.readLine().split(" ");
       n = Integer.parseInt(arr[0]);
       int vv = Integer.parseInt(arr[1]);
       
       //二进制优化初始化
       for(int i=0;i<n;i++){
           String[] arr1 = br.readLine().split(" ");
           int m = Integer.parseInt(arr1[2]);
           int nw = Integer.parseInt(arr1[1]);
           int nv = Integer.parseInt(arr1[0]);
           int k = 1;
           while(m>=k){
               m-=k;
               w[idx]=nw*k;
               v[idx]=nv*k;
               idx++;
               k<<=1;
           }
           if(m>0){
               w[idx]=nw*m;
               v[idx]=nv*m;
               idx++;
           }
       }
       
       n=idx;
       //遍历每一个物品
       for(int i=0;i<n;i++){
           for(int j=vv;j>=0;j--){
               if(j>=v[i])dp[j]=Math.max(dp[j],dp[j-v[i]]+w[i]);
           }
       }
       
       System.out.println(dp[vv]);
       
   }
}

分组背包

把组当成01背包，再来一层循环遍历物品的属性就好了，是一个变型。

线性dp

状态计算的时候，递推有个明确线性的顺序，故而得称”线性dp“。

常见的子序列问题也可归纳为线性dp问题。

数字三角形问题

同样类似的有蓝桥杯的「杨辉三角形」也是这种类似的数字三角形，考虑怎么转换为数组‘

也要注意边界的取值问题

最长上升子序列问题

$O(N^2)$解法

import java.util.*;
import java.io.*;
public class Main{
    static final int N = 1010;
    static int[] dp = new int[N];
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        String[] arr = br.readLine().split(" ");
        int[] nums = new int[n];
        for(int i=0;i<n;i++)nums[i]=Integer.parseInt(arr[i]);
        Arrays.fill(dp,1);
        int res = 1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                if(nums[j-1]<nums[i-1])dp[i]=Math.max(dp[i],dp[j]+1);
            }
            res=Math.max(res,dp[i]);
        }
        System.out.println(res);
    }
}

$O(NlogN)$解法

思路就是能够通过二分来优化$O(N^2)$中的内层寻找倒数第二个，即小于当前最后一个数的过程。

参考代码：

import java.util.*;
import java.io.*;
public class Main{
    static final int N = 100010;
    static int[] handle = new int[N]; //handle[i]存的是长度为i的子序列的集合的末尾的最小值
    static int cnt;
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        String[] arr = br.readLine().split(" ");
        int[] nums = new int[n];
        for(int i=0;i<n;i++)nums[i]=Integer.parseInt(arr[i]);
        
        for(int i=0;i<n;i++){
            int l = 0,r=cnt;
            //二分找到小于nums[i]的最大值
            while(l<r){
                int mid = l+r+1>>1;
                if(nums[i]<=handle[mid])r=mid-1;
                else l=mid;
            }
            handle[l+1]=nums[i];
            if(l==cnt)cnt++;
        }
        System.out.println(cnt);
    }
}

最长公共子序列问题

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 1010;
    static int[][] dp = new int[N][N]; //dp[i][j]代表的是 以由字符串A中1~i组成 B 1~j中组成的所有公共子序列 的最大值
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] arr = br.readLine().split(" ");
        int n = Integer.parseInt(arr[0]);
        int m = Integer.parseInt(arr[1]);
        char[] A = (" "+br.readLine()).toCharArray();
        char[] B = (" "+br.readLine()).toCharArray();
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
				//dp[i-1][j] 和 dp[i][j-1] 已经包含了dp[i-1][j-1]，省略不写
                dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                if(A[i]==B[j])dp[i][j]=Math.max(dp[i][j],dp[i-1][j-1]+1);
            }
        }
        System.out.println(dp[n][m]);
        
    }
}

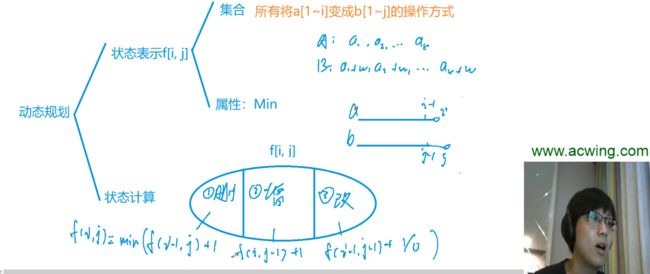
编辑距离问题

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 1010;
    static int[][] dp = new int[N][N];
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine().trim());
        char[] A = (" "+br.readLine()).toCharArray();
        int m = Integer.parseInt(br.readLine().trim());
        char[] B = (" "+br.readLine()).toCharArray();
        //初始化 
        for(int i=1;i<=m;i++)dp[0][i]=i;
        for(int j=1;j<=n;j++)dp[j][0]=j;
        
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                dp[i][j]=0x3f3f3f3f;
                if(A[i]==B[j])dp[i][j]=dp[i-1][j-1];
                dp[i][j]=Math.min(dp[i-1][j]+1,dp[i][j]);   //删
                dp[i][j]=Math.min(dp[i][j-1]+1,dp[i][j]);   //增
                dp[i][j]=Math.min(dp[i-1][j-1]+1,dp[i][j]); //改
            }
        }
        System.out.println(dp[n][m]);
        
    }
}

区间dp

合并相邻区间的题目，考虑使用区间dp。

dp[i][j]状态定义为 合并区间[i,j]为一堆 的 XX属性

因为合并相邻区间，所以我们还需要一个k来代表合并的是[i,k]与[k+1,j]两个相邻区间

因此时间复杂度是$O(N^3)$的 遍历顺序：区间长度->区间左端点->区间划分(l,mid)与(mid+1,r)

题目：石子合并

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 310;
    static int[][] dp = new int[N][N];  //dp[i][j]表示 合并区间[i,j]为一堆 的最小代价
    static int[] S = new int[N];
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        String[] arr = br.readLine().split(" ");
        //O(1)求区间的长度——前缀和数组
        for(int i=1;i<=n;i++){
            S[i]=S[i-1]+Integer.parseInt(arr[i-1]);
        }
        
        //区间dp
        for(int i=0;i<=n;i++)Arrays.fill(dp[i],0x3f3f3f3f);
        for(int i=0;i<=n;i++)dp[i][i]=0;
        
        //大区间合并需要用到小区间，最外层为区间长度
        for(int i=2;i<=n;i++){
            //区间左端点
            for(int j=1;j<=n-i+1;j++){
                //k
                for(int k=j;k<=j+i-2;k++){
                    dp[j][j+i-1]=Math.min(dp[j][j+i-1],dp[j][k]+dp[k+1][j+i-1]+S[k]-S[j-1]+S[j+i-1]-S[k]);
                }
            }
        }
        
        System.out.println(dp[1][n]);
    }
}

计数类dp

题目：整数划分

集合的属性是cnt。有的题目也可以用「背包思路」去做，可以优化成一维数组。

但这里换一种新的思路解决计数类问题：【核心在于去掉1】

• 集合定义为用多少个数的总和的方案数
• 如果最小值为1，那么它的方案数 与 去掉1的方案数 一致
• 如果最小值大于1，那么它的方案数 与 所有数减1的方案数 一致

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 1010;
    static final int MOD = (int)1e9+7;
    static int[][] dp = new int[N][N]; //dp[i][j]代表 用j个数 代表总和为i 的方法数
    public static void main(String[] args)throws Exception{
        BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        dp[1][1]=1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                //        最小值是1，去1方案数不变    最小值不是1，所有数减1方案数不变
                dp[i][j]=(      dp[i-1][j-1]       +              dp[i-j][j]            )%MOD;
            }
        }
        int res  = 0;
        for(int i=1;i<=n;i++)res=(res+dp[n][i])%MOD;
        System.out.println(res);
    }
}

记忆化搜索

dp是循环，记忆化搜索是递归实现。

记忆化搜索思路简单，代码复杂度低，但是存在爆栈的可能性。

滑雪这道题用dp来做就会麻烦一些，用记忆化搜索会清晰很多

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int R = 310,C=310;
    static int[][] dp = new int[R][C];
    static int[][] g;
    static int[][] dirs = {{-1,0},{1,0},{0,1},{0,-1}};
    static int r,c;

    public static int Dp(int x,int y){
        if(dp[x][y]!=-1)return dp[x][y];

        dp[x][y]=1;
        //上下左右四个点
        for(int[] dir : dirs){
            int nx = x+dir[0],ny=y+dir[1];
            if(nx<0||ny<0||nx>=r||ny>=c||g[nx][ny]>=g[x][y])continue;
            dp[x][y]=Math.max(dp[x][y],Dp(nx,ny)+1);
        }
        return dp[x][y];
    }

    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] arr = br.readLine().split(" ");
        //给的样例矩阵中整数都是>=0，可以用-1初始化dp数组
        for(int i=0;i<R;i++)Arrays.fill(dp[i],-1);

        r = Integer.parseInt(arr[0]);
        c = Integer.parseInt(arr[1]);
        g = new int[r][c];
        for(int i=0;i<r;i++){
            String[] arr1 = br.readLine().split(" ");
            for(int j=0;j<c;j++){
                g[i][j]=Integer.parseInt(arr1[j]);
            }
        }

        int res = 1;
        for(int i=0;i<r;i++){
            for(int j=0;j<c;j++){
                res = Math.max(res,Dp(i,j));
            }
        }
        System.out.println(res);        
    }
}

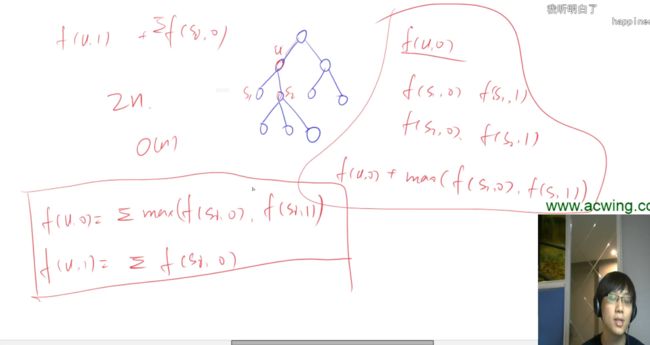
树形dp

感觉树形dp和记忆化搜索差不多，都是封装dp数组用于记忆，进行递归搜索(遍历树)。

于是就把树形dp归到记忆化搜索下面了

题目：没有上司的舞会

参考代码：

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 6010;
    static int[] happy = new int[N];
    static int n;
    static int[] e = new int[N],ne=new int[N],head = new int[N];
    static int idx;
    static boolean[] hasLeader = new boolean[N];
    static int[][] dp = new int[N][2];

    public static void add(int a,int b){
        e[idx]=b;
        ne[idx]=head[a];
        head[a]=idx++;
    }

    public static int getDP(int u,int choose){
        //去掉这个if会TLE，因为会重复计算，浪费时间，有点记忆化搜索的味道（已经把计算结果存进dp数组里了）
        if(dp[u][choose]!=0x3f3f3f3f)return dp[u][choose];
        if(choose==0){
            dp[u][choose]=0;
            //遍历当前节点的所有子节点
            for(int i=head[u];i!=-1;i=ne[i]){
                int son = e[i];
                dp[u][choose]+=Math.max(getDP(son,1),getDP(son,0));
            }

        }else{
            dp[u][choose]=happy[u];
            //遍历当前节点的所有子节点
            for(int i=head[u];i!=-1;i=ne[i]){
                int son = e[i];
                dp[u][choose]+=getDP(son,0);
            }
        }
        return dp[u][choose];
    }

    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        Arrays.fill(head,-1);
        for(int i=0;i<N;i++)Arrays.fill(dp[i],0x3f3f3f3f);
        for(int i=1;i<=n;i++)happy[i]=Integer.parseInt(br.readLine());
        for(int i=0;i<n-1;i++){
            String[] arr = br.readLine().split(" ");
            int l = Integer.parseInt(arr[0]);
            int k = Integer.parseInt(arr[1]);
            // K 是 L 的直接上司
            add(k,l);
            hasLeader[l]=true;
        }

        //找到最大的boss
        int i = 1;
        for(;i<=n;i++)if(!hasLeader[i])break;

        int res = Math.max(getDP(i,1),getDP(i,0));
        System.out.println(res);
    }
}

状态压缩dp

状态是一个整数，但我们要把它看成是一个二进制数，是0是1代表着不同的情况。

因为我们把所有的情况都压缩到一个数里，所以这个数一般不会很大。

状态表示：

• 蒙德里安的梦想：dp[i][j]代表从第 $i-1$ 列伸向第 $i$ 列的 $j$[当前位 代表 行，0代表行没伸，1代表行伸了]
  • 的 所有方案
  • 属性：cnt
• 最短Hamilton路径： dp[i][j]代表从0到 $i$ 的点，经过 $j$[当前位 代表 哪个点，0代表没经过，1代表经过了]
  • 的 所有路径
  • 属性：min

状态计算：

• 蒙德里安的梦想：dp[i][j]+=dp[i-1][k] 如果选法k和选法j不冲突且列满足放置方块的需求
• 最短Hamilton路径：dp[i][j]=dp[k][j-{i}]+a[k][i] 如果经过的所有点j中包含{i}点和{k}点

详细内容：

题目：蒙德里安的梦想

注意这里的boolean[]数组和dp数组 对于不同的n和m来说 都是不能共用的

boolean数组：不同的n（行） 其统计的偶数0也不一样，因此会导致最终n的不一致而boolean的情况不一致。

import java.util.*;
import java.io.*;

public class Main{
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        while(true){
            String[] arr = br.readLine().split(" ");
            int n = Integer.parseInt(arr[0]);  //行
            int m = Integer.parseInt(arr[1]);  //列
            if(n==0&&m==0)break;
            boolean[] isVaild = new boolean[1<<n];
            for(int i=0;i<1<<n;i++){
                int cnt = 0;
                boolean flag = true;
                for(int j=0;j<n;j++){
                    int cur = i>>j;
                    if((cur&1)==0){
                        cnt++;
                    }else{
                        if(cnt%2!=0){
                            flag=false;
                            break;
                        }
                        cnt=0;
                    }
                }
                if(cnt%2!=0)flag=false;
                isVaild[i]=flag;
            }
            long[][] dp = new long[m+1][1<<n];
            dp[0][0]=1;
            for(int i=1;i<=m;i++)
                for(int j=0;j<1<<n;j++)
                    for(int k=0;k<1<<n;k++)
                        if((j&k)==0&&isVaild[j|k])
                            dp[i][j]+=dp[i-1][k];
            System.out.println(dp[m][0]);
        }
    }
}

题目：最短Hamilton路径

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 21;
    static int[][] a = new int[N][N];
    
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        //每个点到其他点都有通路
        for(int i=0;i<n;i++){
            String[] arr = br.readLine().split(" ");
            for(int j=0;j<n;j++){
                a[i][j]=Integer.parseInt(arr[j]);
            }
        }
        int[][] dp = new int[n][1<<n];
        for(int i=0;i<n;i++)Arrays.fill(dp[i],0x3f3f3f3f);
        //dp[i][j] 代表 从0到i节点，路径包含j的节点的最短路径
        dp[0][1]=0;
        //由于基于dp[k][j-{i}]，因此[j-{i}]必须确定为最小值（结果），因此先遍历所有路径
        for(int j=0;j<1<<n;j++){
            for(int i=0;i<n;i++){
                //如果遍历的路径没有i点，跳过
                if((j&(1<<i))==0)continue;
                //递推：dp[i][j]由 dp[k][j-{i}]+a[k][i]得到
                for(int k=0;k<n;k++){
                    //如果j包含k
                    if(((j>>k)&1)==1){
                        dp[i][j]=Math.min(dp[i][j],dp[k][j-(1<<i)]+a[k][i]);
                    }
                }
            }
        }
        System.out.println(dp[n-1][(1<<n)-1]);
    }
}