【电路原理】电路元件基本知识详解
![]()
- 博主简介:努力学习的22级计科生一枚~
- 博主主页: @是瑶瑶子啦
- 所属专栏: 电路理论
前言
- 1.电阻元件
- 2.电容元件
- 3.电感元件
- 4.独立电源
-
- 4.1:电压源
- 4.2:电流源
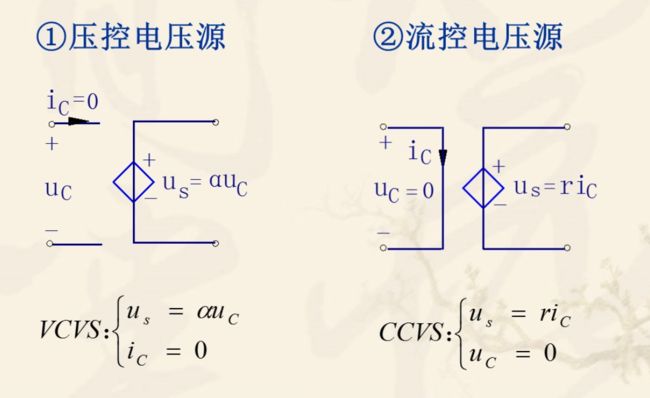
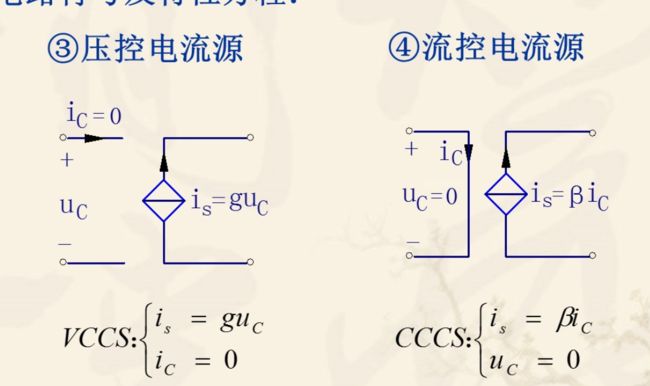
- 5.受控电源
- 6.符号补充:
- 7.总结
本专栏文章主要总结、归纳电路原理、电路理论的知识,以思维导图、表格的方式,清晰的展现知识点。
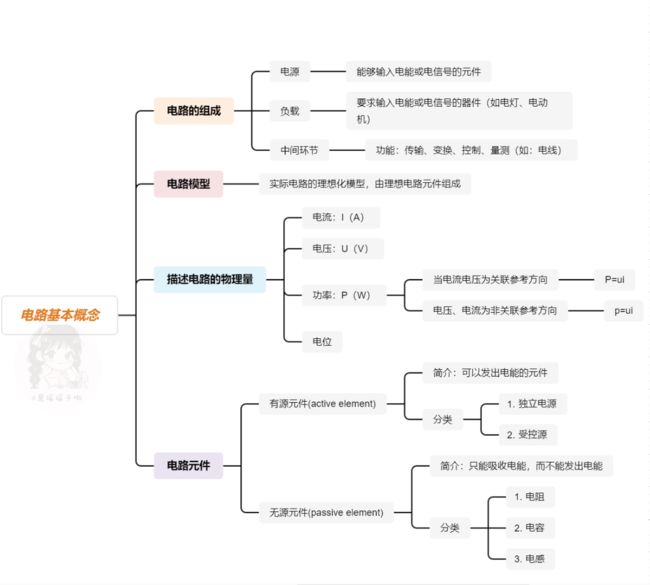
首先我们来了解以下电路中的一些基本概念:
在本节中,主要学习的是电路元件
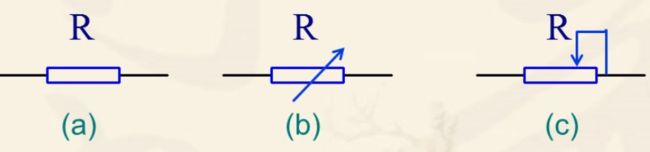
1.电阻元件
❗注意,这里的电阻元件指的线性二端电阻,也就是,即端口电压和电源成比例的二端元件,满足欧姆定律(R=U/I)
3.电磁特性:
所谓电磁特性,指的是端口u-i的特性
| u-i关联,端口特性方程 | u-i非关联,端口特性方程 |
|---|---|
| u = Ri | u = -Ri |
| 当R=0时,u=0,短路 |
另外,还有一个概念叫电导,记为G,G = 1/R
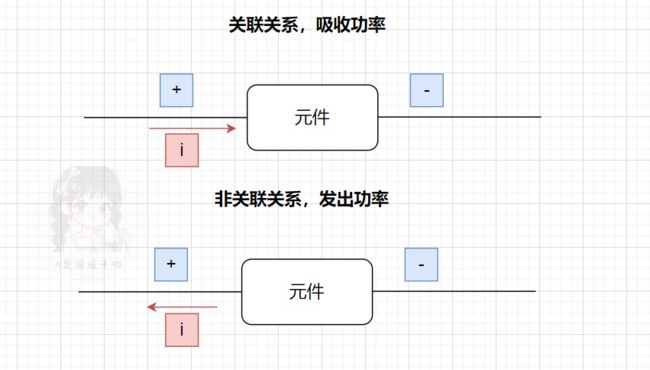
这里补充,什么叫作关联?u,i均有参考方向,这个参考方向是人为设置的(不一定是实际方向),当这两个参考方向一致时,我们称为关联,否则称为非关联。
4.功率与能量
- 功率p:
下面是以关联关系进行的分析
p = ui = Ri^2 = Gu^2
| R>0,则P>0 | R<0,则p<0,实际发出 |
|---|---|
| 实际为吸收功率,无源元件,耗能元件 | 有源元件 |
- 能量w:
∫ − ∞ t p ( x ) d x \int_{-∞}^{t}p(x)dx ∫−∞tp(x)dx
是功率对时间的积分
2.电容元件
注意,此节研究的依然是线性的电容元件,即电荷q和电压u成正比
- 符号表示:C
- 单位:F(法)
1.简介
我们初中和高中听说的电容器就是就是电容元件,电容器是由两块用介质绝缘的电导体构成的,能存储电荷和电场能
2.构成原理
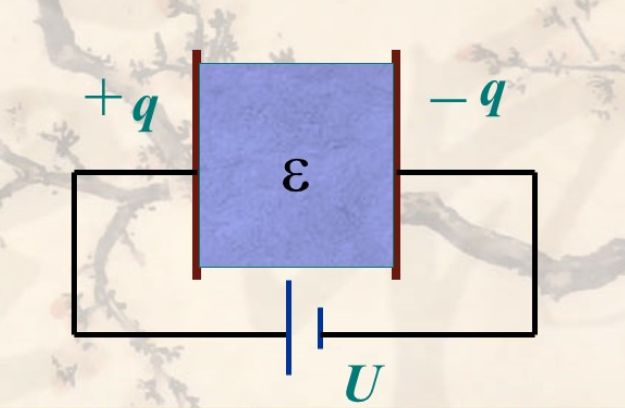
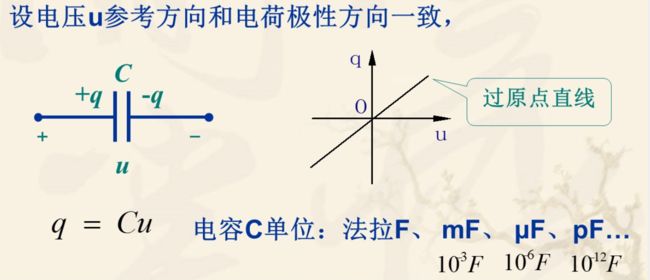
2.电路符号
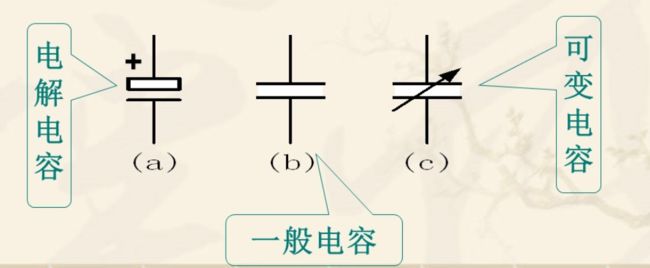
3.电磁特性:q-u
q = C u q=Cu q=Cu
电容:
C = ε S d C = \frac{εS}{d} C=dεS
S为两块极板的正对面积,d为极板之间的距离
i = d q d t = C d u d t i = \frac{dq}{dt}=C \frac{du}{dt} i=dtdq=Cdtdu
u ( t ) = 1 C ∫ − ∞ t i ( t ) d t u(t)=\frac{1}{C} \int_{-∞}^{t}i(t)dt u(t)=C1∫−∞ti(t)dt
可以看到,i是和电压随时间的变化率有关的,成正比关系
同时,从第一个式子我们可以看出,i的表达式是一个微分方程,说明电容器是一个动态元件,第二个式子是i关于t的一个积分方程,说明电容是一个记忆元件
同时,因为在直流电路中(电压u为常数),此时du=0,电容相当于开路/断路
4.储能
下面依旧是按照u-i为关联关系的情况下进行分析
w ( t ) = ∫ − ∞ t p ( t ) d t = ∫ − ∞ t u ( t ) i ( t ) d t = ∫ − ∞ t u ( t ) C d u ( t ) d t d t = 1 2 C u 2 ( t ) ∣ − ∞ t w(t)=\int_{-∞}^{t}p(t)dt=\int_{-∞}^{t}u(t)i(t)dt=\int_{-∞}^{t}u(t)C\frac{du(t)}{dt}dt=\frac{1}{2}Cu^{2}(t)|_{-∞}^{t} w(t)=∫−∞tp(t)dt=∫−∞tu(t)i(t)dt=∫−∞tu(t)Cdtdu(t)dt=21Cu2(t)∣−∞t
假设 u(- ∞ )= 0,有w>=0,则说明电容是无源元件,任一时刻t,电容储能:
w = 1 2 C u 2 ( t ) w = \frac{1}{2}Cu^{2}(t) w=21Cu2(t)
3.电感元件
我们之前所说的线圈,对,就是那种导线绕城,能存储磁场能,的线圈,其实就是一个电感元件
- 符号表示:L
- 单位:H、mH…
1.电感线圈原理示意图
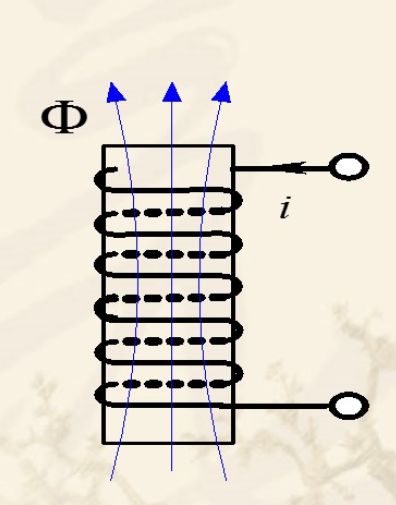
2.电路符号
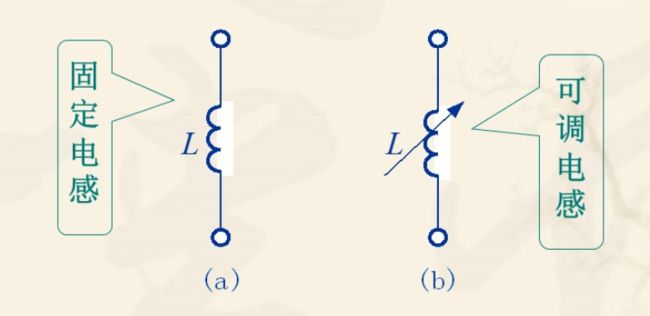
3.电磁特性
电感元件的电磁特性用磁链和电流的关系来表示。ψ-i
线圈中的电流在线圈中激发产生磁场(magnetic field),从而在线圈中形成与电流相交链的磁通φ(flux)
电流i和磁通量φ之间遵守右手螺旋法则。与每匝线圈所交链的磁通量之和称之为该线圈的磁链,记为ψ
公式:
ψ = L i ψ=Li ψ=Li
4.u-i 关系(端口特性
还是以关联关系分析
u = d ψ d t = L d i d t u = \frac{dψ}{dt}=L\frac{di}{dt} u=dtdψ=Ldtdi
可以看出,u和磁通量的变化率或者说电流的变化率有关,说明电感元件是动态元件
i ( t ) = 1 L ∫ − ∞ t u ( x ) d x i(t)=\frac{1}{L}\int_{-∞}^{t}u(x)dx i(t)=L1∫−∞tu(x)dx
可以看出,电流是关于积分方程的表达式,说明电感是一个记忆元件
在直流电路(电流i为常数,di=0),此时电感相当于短路
以t0为计时起点:
i ( t ) = 1 L ∫ − ∞ t u ( x ) d x = i ( t 0 ) + 1 L ∫ t 0 t u ( x ) d x i(t)=\frac{1}{L}\int_{-∞}^{t}u(x)dx=i(t0)+\frac{1}{L}\int_{t0}^{t}u(x)dx i(t)=L1∫−∞tu(x)dx=i(t0)+L1∫t0tu(x)dx
5.储能
关联关系下,电感元件吸收的总能量:
w ( t ) = ∫ − ∞ t p ( x ) t x = ∫ − ∞ t u ( x ) i ( x ) d x = 1 2 L i 2 ( x ) ∣ − ∞ t w(t)=\int_{-∞}^{t}p(x)tx=\int_{-∞}^{t}u(x)i(x)dx=\frac{1}{2}Li^{2}(x)|_{-∞}^{t} w(t)=∫−∞tp(x)tx=∫−∞tu(x)i(x)dx=21Li2(x)∣−∞t
假设i(-∞)=0,则w>0
任一时刻t,电感储能:
w ( t ) = 1 2 L i 2 ( t ) w(t)=\frac{1}{2}Li^{2}(t) w(t)=21Li2(t)
储能对比
| 电容C | 电感 |
|---|---|
| 电能 | 磁能 |
4.独立电源
简介:独立电源是指能独立向外提供电能的电元件,也叫作激励
独立电源有两种电源模型:
- 电压源
- 电流源
接下来我们逐一介绍
4.1:电压源
电压源模型是指有化学电池、稳压电源等的抽象
1.定义
端口电压,即源电压是确定的时间函数,u = u(t),与端口电流无关;端口电流由外电路决定。
源电压可以是常量(如直流电压源U),或者时变量u(t)
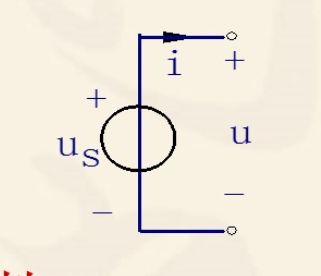
3.端口特性
u = u s u = u_{s} u=us
两端电压是确定的,与外电路没有关系!电流i由外电路确定
当电压源两端电压置为0时,电压源相当于短路
4.功率
这里的前提是非关联情况下:
p = u s i p=u_{s}i p=usi
| p的正负 | 情况 |
|---|---|
| P>0 | 实际输出,电源供电 |
| p<0 | 实际吸收,负载用电 |
4.2:电流源
是光电池、稳流电源的抽象
1.定义
端口电流即源电流i是确定的时间函数:
i s = i ( t ) i_{s}=i(t) is=i(t)
与端口电压无关
2.符号
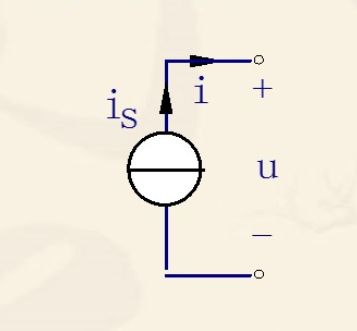
3.端口特性
i = i s i=i_{s} i=is
u由外电路确定
当电流置为0时,电流源相当于开路
4.功率
非关联情况下:
p = u i p=ui p=ui
| p的正负 | 情况 |
|---|---|
| P>0 | 实际输出,电源供电 |
| p<0 | 实际吸收,负载用电 |