数据结构——栈
目录
- 栈的结构
- 栈的实现
-
- 栈的结构体
- 初始化
- 判空
- 入栈
- 出栈
- 取栈顶元素值
- 销毁
栈的结构
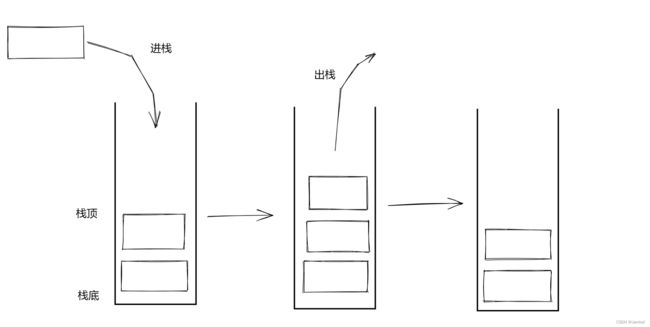
栈是一个特殊的线性表,只允许在固定的一端进行插入和删除操作
进行数据插入和数据删除的一端叫做栈顶,另一端叫做栈底
栈中元素都遵循后进先出LIFO的原则
压栈:在栈顶进行插入的操作
出栈:在栈顶进行删除的操作
所以根据栈的顺序,有一种题,给定一个入栈序列,选出可能或不可能的出栈顺序
假设入栈序列为ABCDE
因为栈的原则是后进先出,所以我们最先想到的结果是EDCBA
但是可以在入栈的过程中出栈:
比如先进一个A,然后将A出栈,再将B入栈,B再出栈,以此类推,最后出栈的顺序就是ABCDE了
所以这种题最稳妥的做法就是一次画图
栈的实现
对于实现栈的结构,我们可以使用数组来实现
根据栈的特点,只会在栈顶出入元素,所以用数组来实现,不会出现挪动数据的现象发生,元素的插入和删除的时间复杂度都是O(1)
同时也可以使用链表结构来实现
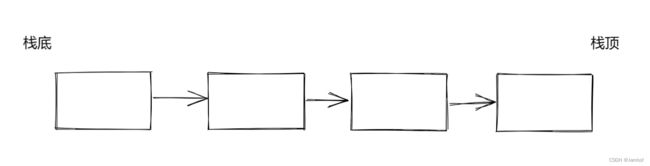
如果使用单链表来实现,头节点作为栈底,尾结点作为栈顶
入栈直接在最后尾插一个结点,时间复杂是O(1),而出栈操作需要找到最后一个节点的前一个节点,需要遍历,复杂度为O(n),想要解决这个问题就需要把结构改为带头双向循环链表,但是带头双向循环链表的结构又有些复杂
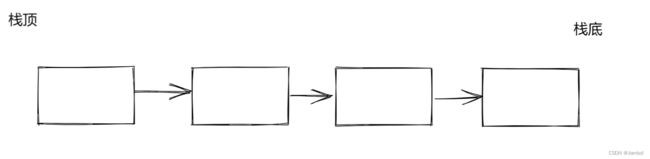
所以我们还有一种更好的解决方法:还是使用单链表,但是头节点作为栈顶,尾节点作为栈底
不论是出栈入栈都直接对头进行操作,时间复杂度为O(1)
从前面看出:用数组和链表实现栈都可以,入栈出栈的时间复杂度都为O(1)
而数组的缓存利用率高,所以使用数组实现是一种更好的选择
下面我们使用数组实现一下栈
栈的结构体
因为使用数组实现,所以这里的结构体与顺序表相似
typedef int STDataType;
#define INITCAPA 4
typedef struct Stack
{
STDataType* a;
int top; //栈顶
int capacity;//容量
}ST;
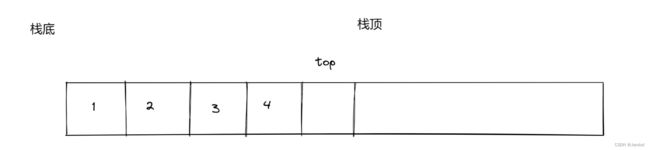
这里的top表示的是栈顶
初始化
初始化,就需要为a开辟空间,然后将capacity赋值,这些都与线性表相同
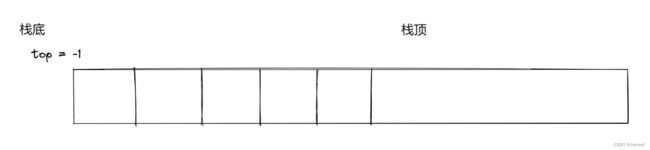
需要注意的一点就是对top初始化的值,可以对top 赋 0 或 -1
如果赋值为0的化,
top就表示栈顶元素的下一个位置
这样在后序的过程中,top一直在栈顶元素的下一个位置
其实,还可以看出:如果top的初始值为0,那么top的值也就是栈中元素的个数
所以这里我选择为top赋初值为0
void STInit(ST* s)
{
assert(s);
s->a = (STDataType*)malloc(sizeof(STDataType) * INITCAPA);
if (s->a == NULL)
{
perror("malloc fail");
return;
}
s->capacity = INITCAPA;
s->top = 0;//top等于0,指的是栈顶元素的下一位置
//s->top = -1; //指的是栈顶元素的位置
}
判空
因为前面为top赋的初值为0,所以当top == 0时,就表示栈为空
bool STEmpy(ST* s)
{
assert(s);
return s->top == 0;
}
入栈
入栈,需要先判断栈满没满,满的条件为s->top== s->capacity,如果满就需要扩容,扩容的过程与顺序表相同
因为top表示栈顶元素的下一位置,所以在top下标处位置进行入数据即可
然后top++ 就完成一次入栈了
void STPush(ST* s,STDataType x)
{
assert(s);
if (s->capacity == s->top)
{
STDataType* tmp = (STDataType*)realloc(s->a, sizeof(STDataType) * s->capacity * 2);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
s->a = tmp;
s->capacity *= 2;
}
s->a[s->top] = x;
s->top++;
}
出栈
出栈,如果栈为空,就会出问题,所以我们可以使用STEmpy函数判断一下栈是否为空
想要出栈,其实只要s->top--即可,top值减1,那么在其他操作中就访问不到最后一个元素,就达到了出栈效果
void STPop(ST* s)
{
assert(s);
assert(!STEmpy(s));
s->top--;
}
这里的出栈函数只是将栈顶的元素出栈,并没有返回栈顶元素的值,想要返回栈顶元素的值,要配合下面的取栈顶元素值函数才行
其实这么设计是遵循C++STL中的函数,在STL中,出栈函数也是不能返回取栈顶元素值的
取栈顶元素值
如果栈为空,无法返回值,就出问题了,所以还要使用STEmpy判空
top是栈顶元素的下一个位置,所以top-1才是栈顶元素的下标
所以返回s->a[s->top-1]的值即可
STDataType STTop(ST* s)
{
assert(s);
assert(!STEmpy(s));
return s->a[s->top - 1];
}
这里的STTop是可以配合着STPop函数使用的,先用STTop返回栈顶元素,然后再用STPop函数将栈顶元素出栈
下面是用STTop和STPop对栈中的值进行打印:
void print(ST* s)
{
int num = s.top;
while (num--)
{
printf("%d\n",STTop(&s));
STPop(&s);
}
}
销毁
void STDestroy(ST* s)
{
assert(s);
free(s->a);
s->a == NULL;
s->capacity = 0;
s->top = 0;
}