排序算法——快速排序（C语言多种实现及其优化策略）

总述

快速排序可以说是排序界的大哥的存在，在c库中的qsort和c++库中的sort两个排序底层都是用快速排序实现，可想快速排序是有多么强大了把哈哈！

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

---

了解过二叉树的佬们肯定一眼就可以看出来，快速排序的思想和二叉树前序遍历的规则非常像，因此，大家在学习快速排序的时候，可以先将基本框架搭好之后，再考虑单趟排法带入即可。

快速排序递归框架

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
   if(right - left <= 1)
       return;
   
   // 按照基准值对array数组的 [left, right)区间中的元素进行划分
   int div = partion(array, left, right);
   //partion为单趟快速排序的封装
   // 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
   // 递归排[left, div)
   QuickSort(array, left, div-1);
   
   // 递归排[div+1, right)
   QuickSort(array, div+1, right);
}

这里的思路很好理解，还有一个细节：
一趟快速排序之后能确定div在排完序之后的位置，所以不用继续对其进行处理，原因也很简单，div下标左边的数都比其小，右边的数都比其大。

单趟快速排序

一共有三种单趟排序的方法，这里一一进行讲解。
由于下面三种做法都需要使用swap函数，所以这里对其进行了封装。

void swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

hoare法

这个单趟排法也是快速排序的发明者hoare所发明的方法，具有开创性作用。
大家可以通过一张动图来理解这一过程：

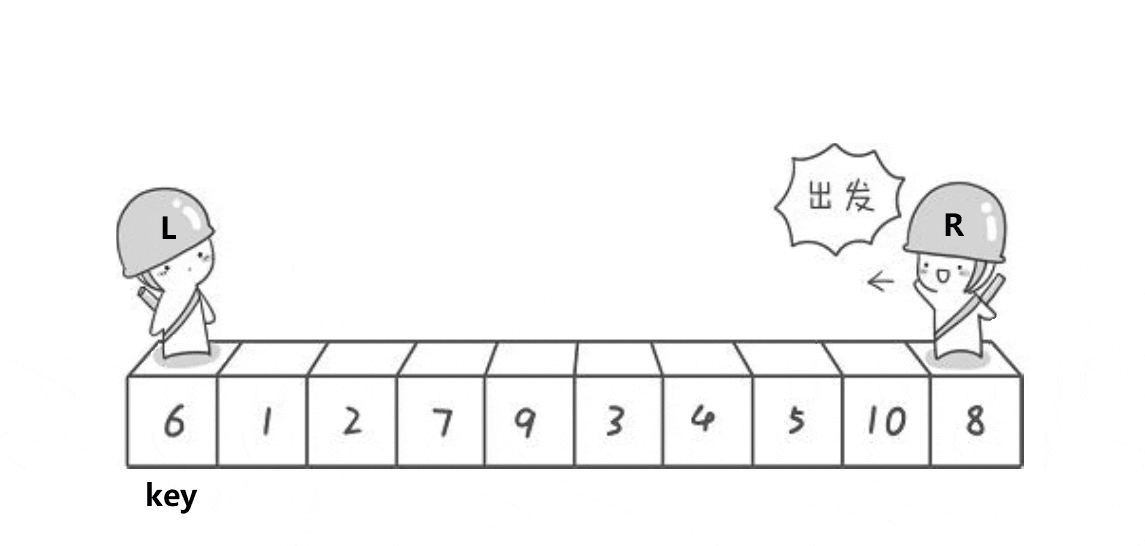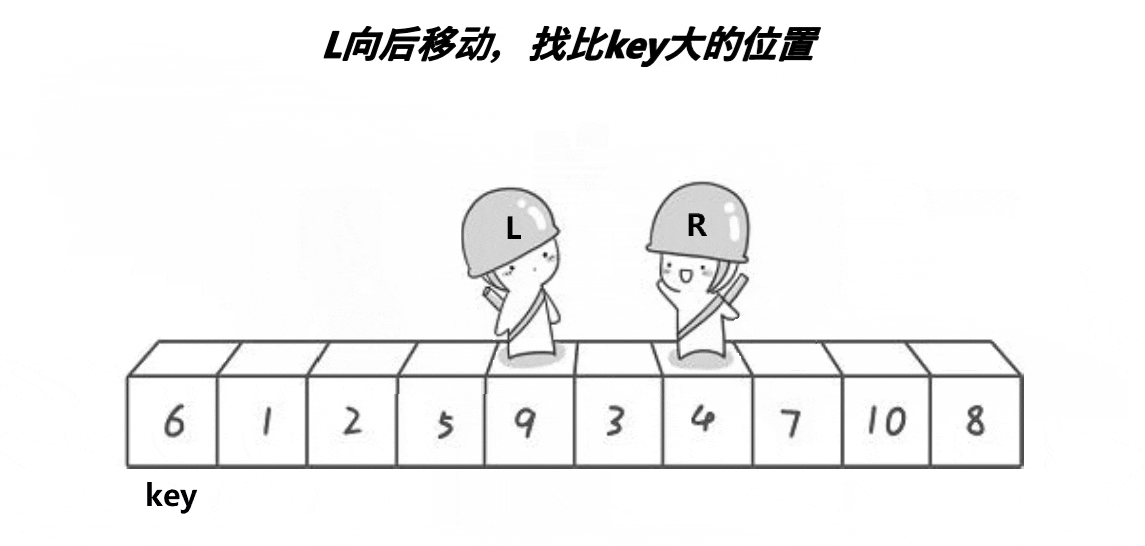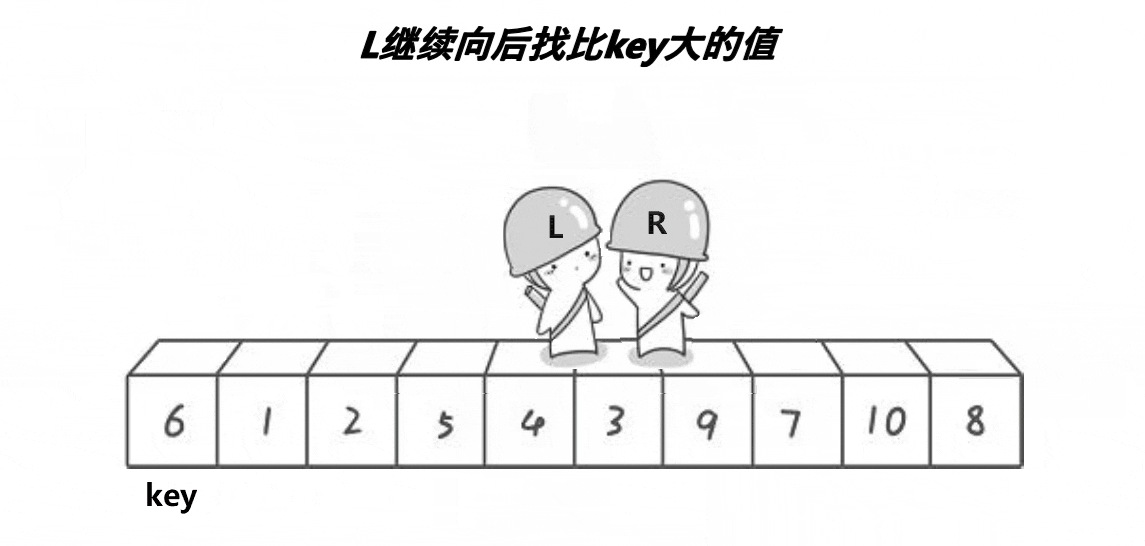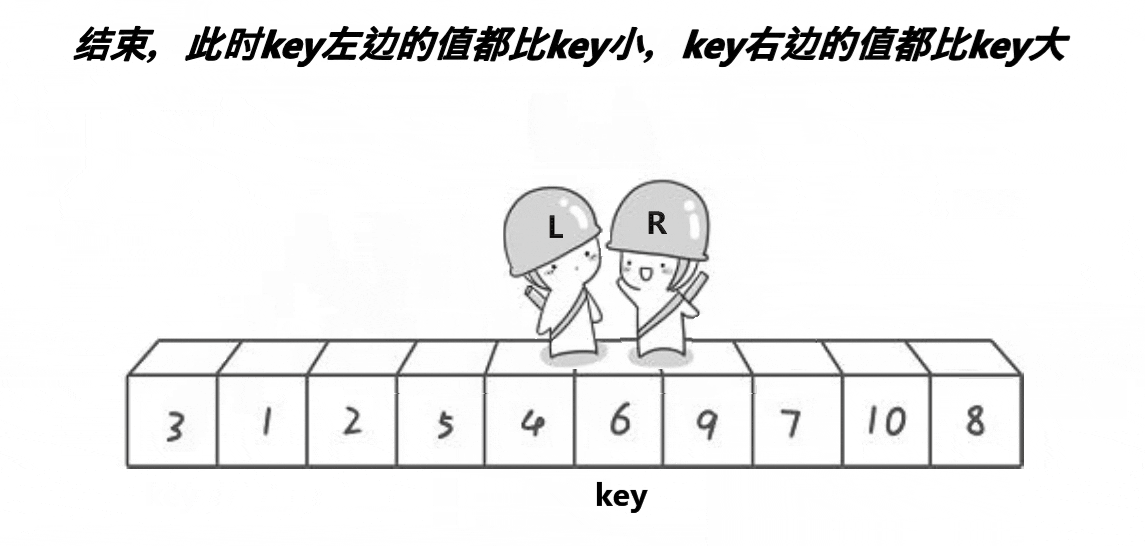
大体思路：在左右两端都设置一个索引，并且选择待排序部分的第一个数做key，右索引先往前走找到比key小的数，接着左索引向后走找到比key大的数，然后交换两数，接着继续这一过程直到left和right相遇，然后将相遇点的位置和左端位置进行交换即完成。

代码如下：

//hoare法
int partSort1(int* a, int begin, int end)
{
	int keyi = begin;
	while (begin < end)
	{
		//前进的时候必须把等于带上，否则当left和right都和key相等时程序就会死循环
		//并且等于的时候位置是不用变的，在原位也能满足快速排序的要求
		// （快速排序只需要左边的数小于等于，右边的数大于等于）
		//并且为了防止某些情况移动时超出数组范围，所以内部移动也需要限制
		while (end > begin &&a[end] >= a[keyi])
			end--;
		while (end > begin &&a[begin] <= a[keyi])
			begin++;
		swap(&a[begin], &a[end]);
	}
	swap(&a[begin], &a[keyi]);
	return begin;
}

这里有一个问题，为什么左边做key就一定要从右边先走？

原因是左边做key，从反方向走能保证相遇时两索引指向的数比key指向的数小，这样完成交换之后才能满足快速排序单趟排序的要求。
下面用分类的方法来验证一下为什么能够满足上面的问题：
分析最后一步，相遇时有两种情况，left走向right，right走向left。

• 若时left走向right，根据该算法，其上一步是right找比key小的数，则一定有a[right]比a[keyi]大，也就是说right指向的数一定要比keyi指向的数来的小，满足题目所需。
• 若是right走向left，同样根据该算法，其上一步是swap(&a[left],&a[right])，并且交换之后left指向的数小于a[keyi]，所以同样满足要求。

这是快速排序的最初版本，但是由于其细节较多导致比较不好控制，因此后面的大佬又研发出了更好理解的两种方法，下面继续进行讲解。

---

挖坑法

挖坑法的大体做法与hoare法相差不大，这里还是用一张动图让大家体会一下。

挖坑法比hoare好的一点在于挖坑法更好理解为什么要从右边先走，左边挖坑右边填，这很符合逻辑（doge），因此改进并不是很大，主要是更好理解。
实现代码：

int partSort2(int* a, int begin, int end)
{
	int left = begin, right = end;
	//保存原坑位的数据，避免“填坑“后数据丢失
	int hole = a[begin];
	while (left < right)
	{
		while (right > left && a[right] >= hole)
			--right;
		a[left] = a[right];
		while (right > left && a[left] <= hole)
			++left;
		a[right] = a[left];
	}
	//将刚开始保存的值填到最后的坑位上
	a[left] = hole;
	return left;
}

前后指针法

这一方法和前面两种方法有了本质上的区别，前后指针的核心就前后指针之间维护了一片数据，这片数据的特点是都比a[keyi]更大，然后在遍历数组的时候不断维护这一个区间，将这片区间不断往后推，即将大的数往后推，小的数往前翻，同样先用一张动图带大家大致的了解一下。

这种排序方法相对于前面两种方法没有那么多的"坑"，并且代码也更加简洁，因此本人更推荐这种写法，接下来上代码让大家感受一下哈哈！
实现代码：

int partSort3(int* a, int begin, int end)
{
	int left = begin, right = begin + 1;
	int key = begin;
	while (right <= end)
	{
		//版本一
		/*if (a[right] < a[key])
			swap(&a[++left], &a[right]);*/

		//版本二(运用语法特性)
		//如果前一个条件不成立，那么就不会执行第二个条件
		if (a[right] < a[key]&&++left<right)
			swap(&a[left], &a[right]);
		++right;
	}
	swap(&a[left], &a[key]);
	return left;
}

怎么样，确实简洁很多把！
到此，再把快排的框架部分的partion函数改成这三种函数的其中一个，快速排序就已经完成了，但是请大家再思考一下，现在的排序有没有什么缺陷？

---

快排改进

key的选取

首先，我们可以思考一下，如果快速排序排的是一个有序的数组会出现什么情况呢？

不难发现，如果是有序的情况，快速排序的效率将会直逼$O(n^2)$,效率极其低下，并且如果数据量过多，由于快速排序使用递归的写法，还有可能出现爆栈的状况，这是我们最不想看到的事。

而造成这样的原因，就是key的选取问题，很容易能够发现，如果每次key的选取都是该部分中排名中等的数，那么快排的效率将会达到最大，而如果是最大或者最小的数，快排的效率将会极低，因此为了解决这一个问题，就需要改进key的选取方式，不能每次都是选取的最左边。
这里有两种方法，随机选key和三数取中法，下面进行一一讨论。

随机选key

我们每次随机选取区间中的一个数，将其与其最左边的数交换，接着再进行排序，就可以比较好解决这一问题。下面的改进都在第三种快排方法进行改进。

具体代码：

**注意：**要使用rand()函数，C语言中需要包含头文件，并且需要在main()函数调用srand()函数

int partSort3(int* a, int begin, int end)
{
	int left = begin, right = begin + 1;
	
	//随机选key
	int randI = rand()%(right - left) + left;
	if (randI != left)
		swap(&a[midI], &a[left]);
		
	int key = begin;
	while (right <= end)
	{
		//版本一
		/*if (a[right] < a[key])
			swap(&a[++left], &a[right]);*/

		//版本二(运用语法特性)
		//如果前一个条件不成立，那么就不会执行第二个条件
		if (a[right] < a[key]&&++left<right)
			swap(&a[left], &a[right]);
		++right;
	}
	swap(&a[left], &a[key]);
	return left;
}

三数取中

三数取中的思路其实很简单，就是选出区间中间的数以及两端的数中排行第二的数与第一个数进行交换，这种做法在有序的情况下优化最大，因为有序状态下能搞保证三数取中后所选出的key值能让下一次平均划分区间。

三数取中的代码如下：

int findMid(int* a, int begin, int end)
{
	int mid = (begin + end) / 2;
	if (a[begin] > a[mid])
	{
		if (a[mid] > a[end])
			return mid;
		else if (a[begin] > a[end])
			return end;
		else
			return begin;
	}
	else
	{
		if (a[mid] < a[end])
			return mid;
		else if (a[begin] > a[end])
			return begin;
		else
			return end;
	}
}

将其带入快排单趟之后：

int partSort3(int* a, int begin, int end)
{
	int left = begin, right = begin + 1;
	int midI = findMid(a, begin, end);
	if (midI != left)
		swap(&a[midI], &a[left]);
	int key = begin;
	while (right <= end)
	{
		//版本一
		/*if (a[right] < a[key])
			swap(&a[++left], &a[right]);*/

		//版本二(运用语法特性)
		//如果前一个条件不成立，那么就不会执行第二个条件
		if (a[right] < a[key]&&++left<right)
			swap(&a[left], &a[right]);
		++right;
	}
	swap(&a[left], &a[key]);
	return left;
}

小区间优化

这部分优化运用了插入排序的知识，如果不了解的老铁可以先看看这篇文章：
插入排序详解

考虑数据很少的时候，如果用快速排序，那么递归消耗和直接使用插入排序哪个效率更高。
由于递归的消耗，当区间个数较小时，其效率是远远比不上插入排序的，并且递归的深度越大，所消耗的时间占比越多。
参考下图：

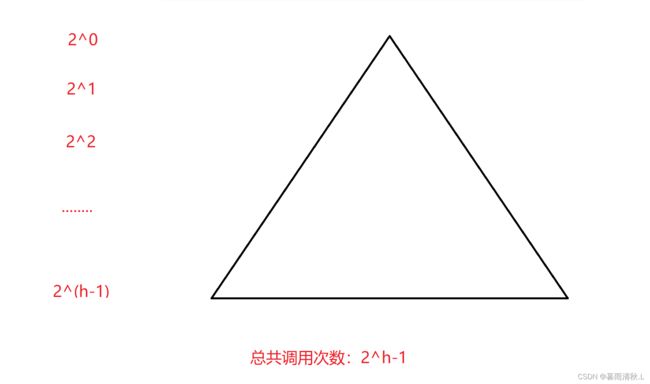
最理想状态下，快速排序的递归调用中最后一层的调用次数占了总调用次数的1/2，这是非常恐怖的，也就是说如果当区间较小的时候采取插入排序来替代快速排序，将会减小一半以上的递归调用次数，这里性能就又有了很大的提升。

因此，当区间数据数量小于一定值时，就可以用插入排序来代替快速排序，代码如下：

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
   if(right - left <= 1)
       return;
   //当区间个数大于10个时，继续走快速排序
   if(right - left + 1 > 10)
   {
   		// 按照基准值对array数组的 [left, right)区间中的元素进行划分
   		int div = partSort(array, left, right);
   		//partion为单趟快速排序的封装
  	 	// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
   		// 递归排[left, div)
   		QuickSort(array, left, div-1);
   		// 递归排[div+1, right)
   		QuickSort(array, div+1, right);
   }
   else
   {
   		//这里需要注意的就是由于区间不一定是从数组的头开始，所以起始点应该设置为array+begin
   		//数据个数是end-begin+1
   		//关于插入排序的代码在上一篇博客，如果不了解的可以查看上一篇
   		insertSort(array+begin,end - begin + 1);
   }
}

面对多个重复数据时的乏力

想像一下，如果待排序的数是几百万的重复数字的话，光靠随机选key或者三数取中能防止爆栈吗？
答案显而易见，是不能的，所以这里还需要一种方法就是三路划分，通过这个技巧就能完美的解决这一问题。

关于三路划分的思想以及三路划分如何实现，博主这里偷个懒（doge），转载一下csdn上看到的一个佬的文章（主要是写的真的不错hhh），本人的三路递归就是学习这个文章的。
文章链接：来自csdn佬的三路划分

但是这个佬在文章中并没有给出三路划分的实现代码，这里给出我的实现代码：(完整快速排序)

void QuickSort(int* a, int begin, int end)
{
	int left = begin, right = end;
	if (begin >= end)
		return;
	//小区间优化
	//当待处理的子区域很小时，用插入排序效果更好
	/*if (end - begin + 1 > 10)
	{*/
		//int mid = partSort1(a, begin, end);
		//int mid = partSort2(a, begin, end);
		//int mid = partSort3(a, begin, end);	//用一个指针指向最后面，然后让一个指针不断向前走
	//把大的数往后推，小的数往前进
		int mid = findMid(a, begin, end);
		if (mid != begin)
			swap(&a[begin], &a[mid]);
		int keyi = begin;
		int cur = begin + 1;
		int less_end = begin + 1, great_head = end;
		while (cur <= great_head)
		{
			while (cur <= great_head && a[cur] > a[keyi])
				swap(&a[cur], &a[great_head--]);
			if (a[cur] < a[keyi])
				swap(&a[cur], &a[less_end++]);
			++cur;
		}
		swap(&a[less_end - 1], &a[keyi]);
		QuickSort(a, begin, less_end-1);
		QuickSort(a, great_head + 1, end);
	//}
	/*else
		InsertSort(a + begin, end - begin + 1);*/
}

---

以上就是快速排序的所有内容了，如果有哪里写的有问题，还请大家评论区中指出！