Map和Set
文章目录
1.二叉搜素树
2.TreeMap、TreeSet
3.HashMap、HashSet
二叉搜索树的定义:
二叉搜索树是指左结点比根结点小的结点,右结点比根节点大的一种树形的数据结构。
单分支的情况:
这是右单只,当然也有左单只。
二叉搜索树:如果左右分支都有时间复杂度为log2N ,如果是单分支的情况,时间复杂度为O(N)
二叉搜索树找某个结点:
public TreeNode search(int cur) {
//TreeNode head = creat();
TreeNode c=this.head;
while (c != null) {
if (c.val > cur) { //结点的数值大于要找的数值就去结点的左子树找,反之去结点的右子树找。
c = c.left;
} else if (c.val < cur) {
c = c.right;
} else {
return c;
}
}
return null;
}二叉搜索树插入某个结点:
public void offer(int cur)
{
TreeNode m=new TreeNode(cur);
if(this.head==null) {
this.head=m;
return;
}
TreeNode c=this.head;
TreeNode parent=null;
//TreeNode head = creat();
while(c!=null)
{
parent=c;
if (c.val > cur) {
c = c.left;
} else if(c.val < cur) {
c = c.right;
} else { //如果要插入的数据已存在,就不需要再插入了。
System.out.println("有相同的数据无法插入");
}
}
去找叶子结点,根据要插入结点数值的大小和叶子结点大小比较,来确定是放在叶子结点这个根结点的左结点还是右结点。
if(cur>parent.val)
{
//m=parent.right;
parent.right=m;
return;
}
else
{
parent.left=m;
return;
}
}二叉搜索树删除某个结点:
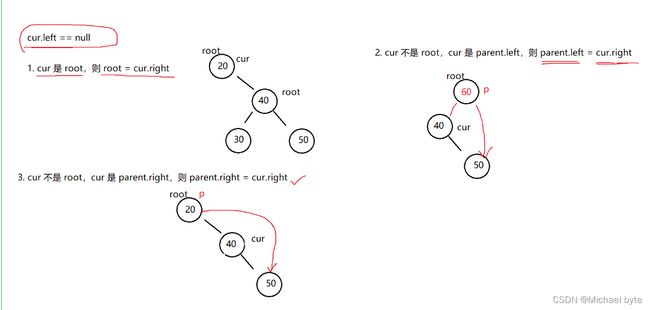
可以总体上分为三种情况:
假设要删除的结点为cur,
1.cur.left==null;
2.cur.right==null;
3.cur.right!=null&&cur.left!=null
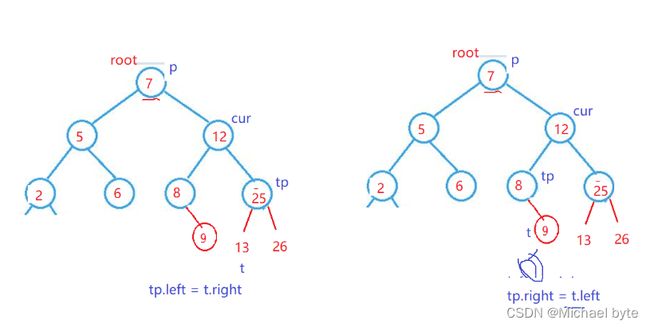
像这种情况我们主要采用替罪羊的方式进行删除:我们可以找要删除接点左子树的最大结点或者要删除结点右子树最小结点来替代要删除的结点:
像这种情况我们知道9或者13都可以替代12,那问题是我们应该如何删除9或者13呢?
我们知道9的左右要么都为空,要么只有左结点,因为9已经是12这个要删除结点的左子树的最大值了,那么9就不可能再有右结点了,这时只需tp.right=t.left就可以删除9这个结点了
同理13要么左右都为空,要么只有右结点,这时只需tp.left=t.right就可以删除了。
这里还有一种特殊情况需要考虑:8或者25没有结点:
public void remove(int cur)
{
TreeNode c=this.head;
TreeNode parent1=null;
while (c != null) {
if (c.val > cur) {
parent1=c;
c = c.left;
} else if (c.val < cur) {
parent1=c;
c = c.right;
} else {
if(c.left==null)
{
if(c==this.head)
{
head=c.right;
}
else if(parent1.left==c)
{
parent1.left=c.right;
}
else
{
parent1.right=c.right;
}
}
else if(c.right==null)
{
if(c==this.head)
{
head=c.left;
}
else if(parent1.left==c)
{
parent1.left=c.left;
}
else
{
parent1.right=c.left;
}
}
else {
TreeNode target=c.left;
TreeNode tp=c;
while(target.right!=null) //去左子树找最大值
{
tp=c;
target=target.right;
}
c.val=target.val; //将左子树最大值赋值给要删除的结点
if(tp.right==target) {
tp.right = target.left;
}
else
{
tp.left=target.left; //这种情况要注意此时要删除的结点左节点没有结点了。
}
}
}
}
}
TreeMap是一种数据结构,里面存有关键字Key,和关键字对应的值Value.
TreeMap底层是红黑树,红黑树具备二叉搜索树的基本特性,其时间复杂度为log2N,因此TreeMap里的Key值必须是可比较的,且必须是唯一的,Value值可以不是唯一的,可以修改,key值不可以修改,且Key值不能为null。
Map.Entry
键值对遍历的方式一般有两种:
public static void main(String[] args) {
TreeMapa=new TreeMap<>();
a.put("xiaofang",1);
a.put("xiaohai",2);
a.put("xiaosun",3);
System.out.println(a); public static void main(String[] args) {
TreeMapa=new TreeMap<>();
a.put("xiaofang",1);
a.put("xiaohai",2);
a.put("xiaosun",3);
//System.out.println(a);
Set>m=a.entrySet();
for(Map.Entryl:m)
{
System.out.println("Key:"+l.getKey()+' '+"Value:"+l.getValue());
}
}
TreeMap可以用来解决Key的次数问题:用Value表示Key的次数,比如查英语每个单词出现的个数:英语单词可以用Key来表示,Value表示这个单词出现的个数。
我们来看一个例题:
像这道题我们可以用TreeMap来存储每个数及其出现的次数。
HashMapb=new HashMap<>();
int i=0;
for(i=0;i>c=b.entrySet();
for(Map.Entryl:c)
{
if(l.getValue()>=2)
{
return true;
}
}
return false; TreeSet
1.TreeSet里面只有Key没有Value,且Key值是唯一的,Key值不能是null,不能修改。
由TreeSet的源码我们可以看到TreeSet的底层其实是TreeMap来实现的,所以Key值是唯一的,不能为null,不能被修改。
TreeSet最大的作用是去重。
public static void main(String[] args) {
TreeSeta=new TreeSet<>();
int[]arr={1,1,3,3,4,4};
for(int i=0;i 哈希表:哈希表是一种查找、插入数据时间复杂度可以达到O(1)的数据结构
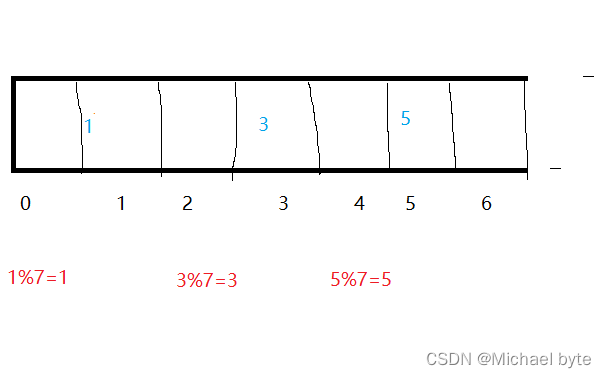
哈希函数:常用 hash(key)=key%数组容量
假设我们存的数据Key分别为1 3 5
计算出来的哈希码值就是要存放Key值的数组下标。
那么我们再想另一个问题:如果是8的话 8%7=1那是不是也放在1下标,那这样不就冲突了吗?
其实像这种冲突是无法避免的,我们可以采用一些方法来解决这些冲突。
常用的方法有:线性探测法,二次探测法,而我们java当中常用的是开链法,也叫链地址法。
(数组+链表+红黑树)
像这种情况我们知道 3%7=3 10%7=3,3 和7 都放在同一个位置上,这时候我们就用链地址法,再数组下标3的位置后形成一个链表把元素用链表的形式存储。
hashcode和equals的qe:hascode是指对象的哈希码,equals判断的是两个对象的内容是否相同,两个对象的hashcode一样,equals不一定一样,两个对象的equals一样,hascode一定一样。
eHashMap底层是哈希桶,其时间复杂度为在不冲突情况下是O(1) ,HashMap里面的Key值和Value值可以是null,Key值可以是不具备比较关系的
当Key值一样时,新的键值对的Value会覆盖旧的Value
HashSet底层是HashMap,其存放的Key可以是null,Key可以是不具备大小比较关系的。
HashMap的实现:
class HashMap{
class Node
{
int val;
Node next;
int key;
public Node(int key,int val) {
this.val = val;
this.key=key;
}
}
Node[]arr=new Node[8];
public int usesize;
public void creat(int key,int val)
{
//Node b=new Node(key,val);
int c=key%arr.length;
Node cur=arr[c];
while(cur!=null)
{
if(cur.key==key)
{
cur.val=val;
return;
}
cur=cur.next;
}
Node b=new Node(key,val);
b.next=arr[c];
arr[c]=b;
this.usesize++;
if(load()>0.75) //当负载因子大于0.75时,我们进行扩容
{
kuorong();
}
}
public double load()
{
return (this.usesize)*1.0/this.arr.length;
}
public int search(int key)
{
int d=key%arr.length;
Node m=arr[d];
while(m!=null)
{
if(m.key==key)
{
return m.val;
}
m=m.next;
}
return -1;
}
public void kuorong()
{
Node[]t=new Node[2*arr.length];
int i=0;
for(i=0;i泛型的形式:
class Hash3
{
class Node
{
V val;
Node next;
K key;
public Node(K key,V val) {
this.val = val;
this.key=key;
}
}
Node[]arr=(Node[])new Node[8];
public int usesize;
public void creat(K key,V val)
{
//Node b=new Node(key,val);
//K c=key%arr.length;
int hash=key.hashCode();//获取hash码值
int c=hash%arr.length;
Node cur=arr[c];
while(cur!=null)
{
if(cur.key.equals(key))
{
cur.val=val;
return;
}
cur=cur.next;
}
Node b=new Node<>(key,val);
b.next=arr[c];
arr[c]=b;
this.usesize++;
/*if(load()>0.75)
{
kuorong();
}
}
public V search(K key)
{
//int d=key%arr.length;
int ma=key.hashCode();
int d=ma%arr.length;
Node m=arr[d];
while(m!=null)
{
if(m.key.equals(key))
{
return m.val;
}
m=m.next;
}
return null;
}
我们来看一下HashMap底层的源码:
我们可以看到HashMap底层有两个有参的构造方法:一个是 两个参数的,一个是一个参数的,但其实第二个构造方法还是指向第一个构造方法:当我们传一个19时,数组大小的容量会不会是19呢?我们继续来看:
我们看到其实返回的是一个最接近给的参数的2次幂的值,取大于等于的,那就是32.
当我们调用不带参数的构造方法:
我们会发现HashMap并没有数组开辟内存,那到底啥时候开辟的呢?
我们可以发现是在第一次put的时候,数组开辟的容量 为默认的容量,也就是16.
由这张源码,我们可以看到当数组容量大于8,链表的长度大于64时,链表会变成红黑树。
由这张源码我们可以看到:当没有 实现comparable 这个接口的时候,其实是在比较两个对象的hash码值,当实现了的时候:
则按照自己指定的比较规则进行比较。