21天力扣打卡记录
力扣打卡
力扣打卡第一天
题目
给你两个字符串 word1 和 word2 。请你从 word1 开始,通过交替添加字母来合并字符串。如果一个字符串比另一个字符串长,就将多出来的字母追加到合并后字符串的末尾。
返回 合并后的字符串 。
示例 1:
输入:word1 = "abc", word2 = "pqr"
输出:"apbqcr"
解释:字符串合并情况如下所示:
word1: a b c
word2: p q r
合并后: a p b q c r
示例 2:
输入:word1 = "ab", word2 = "pqrs"
输出:"apbqrs"
解释:注意,word2 比 word1 长,"rs" 需要追加到合并后字符串的末尾。
word1: a b
word2: p q r s
合并后: a p b q r s
示例 3:
输入:word1 = "abcd", word2 = "pq"
输出:"apbqcd"
解释:注意,word1 比 word2 长,"cd" 需要追加到合并后字符串的末尾。
word1: a b c d
word2: p q
合并后: a p b q c d
提示:
1 <= word1.length, word2.length <= 100word1和word2由小写英文字母组成
思路,定义一个word3和一个指针i,当指针i大于任何一个给定的字符串长度则结束,随后将剩余字符串补充到定义的word3。
class Solution {
public:
string mergeAlternately(string word1, string word2) {
string word3="";
int i=0;
for(;i<word1.size();i++){
if(i>=word2.size())
break;
word3=word3+word1[i]+word2[i];
}
while(i<word1.size())
{
word3+=word1[i];
i++;
}
while(i<word2.size())
{
word3+=word2[i];
i++;
}
return word3;
}
};
力扣打卡第二天
给定一个数组 nums ,将其划分为两个连续子数组 left 和 right, 使得:
left中的每个元素都小于或等于right中的每个元素。left和right都是非空的。left的长度要尽可能小。
在完成这样的分组后返回 left 的 长度 。
用例可以保证存在这样的划分方法。
思路:
left 中的每个元素都小于或等于 right 中的每个元素翻译为只要所有左边元素的最大值>=所有右边元素的最小值
因此,对于右边的最小值可以定义一个数组,从后向前建立 minright[n-1]=nums[n-1]; minright[i]=min(nums[i],minright[i+1]);
对于左边的最大值 可以每次入队比较 maxleft=max(nums[i],maxleft);
一次遍历即可结束,时间复杂度O(n);
代码如下
class Solution {
public:
int partitionDisjoint(vector<int>& nums) {
int n = nums.size();
vector<int> minright(n);
minright[n-1]=nums[n-1];
for(int i =n-2;i>0;i--){
minright[i]=min(nums[i],minright[i+1]);
}
int maxleft =0;
for(int i=0;i<n-1;i++){
maxleft=max(nums[i],maxleft);
if(maxleft<=minright[i+1]){
return i+1;
}
}
return n-1;
}
};
力扣打卡第三天
给你一个大小为 n x n 的二元矩阵 grid ,其中 1 表示陆地,0 表示水域。
岛 是由四面相连的 1 形成的一个最大组,即不会与非组内的任何其他 1 相连。grid 中 恰好存在两座岛 。
你可以将任意数量的 0 变为 1 ,以使两座岛连接起来,变成 一座岛 。
返回必须翻转的 0 的最小数目。
示例 1:
输入:grid = [[0,1],[1,0]]
输出:1
示例 2:
输入:grid = [[0,1,0],[0,0,0],[0,0,1]]
输出:2
示例 3:
输入:grid = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
输出:1
提示:
n == grid.length == grid[i].length2 <= n <= 100grid[i][j]为0或1grid中恰有两个岛
思路如下:
先找到找到一座岛,然后从岛屿的边缘开始进行地BFS(广度优先)搜索,每次只前进一步,遇到另外一个岛屿,则代表两个岛屿之间连通,返回步数,同时,最短步数即最短的桥。时间复杂度O(n2)
代码如下:
class Solution {
public:
int shortestBridge(vector<vector<int>>& grid) {
int dir[4][2]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//四个方向
int n = grid.size(), m = grid[0].size();
deque<int> st, st2;
//从一个岛开始
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] == 1) {
st.push_back(i * 1000 + j);
grid[i][j] = -1;
break;
}
}
if (!st.empty()) break;
}
// 扩展全岛入队
while (!st.empty()) {
int cur = st.front(); st.pop_front(); st2.push_back(cur);
int x = cur / 1000, y = cur % 1000;
for (int p = 0; p < 4; ++p) {
int i = x + dir[p][0], j = y + dir[p][1];
if (i < 0 || i >= n || j < 0 || j >= m) continue;
if (grid[i][j] == 0 || grid[i][j] == -1) continue;
st.push_back(i * 1000 + j);
grid[i][j] = -1; // 原地标记一下已访问位置
}
}
// 分步 BFS 找最短路
for (int step = 0; !st2.empty(); ++step) {
// one step
for (int k = 0, s = st2.size(); k < s; ++k) {
int cur = st2.front(); st2.pop_front();
int x = cur / 1000, y = cur % 1000;
for (int p = 0; p < 4; ++p) {
int i = x + dir[p][0], j = y + dir[p][1];
if (i < 0 || i >= n || j < 0 || j >= m) continue;
if (grid[i][j] == -1) continue;
if (grid[i][j] == 1) return step;
st2.push_back(i * 1000 + j);
grid[i][j] = -1;
}
}
}
return -1;
}
};
力扣打卡第四天
题目:
给你一个整数数组 nums 和一个整数 k ,找出 nums 中和至少为 k 的 最短非空子数组 ,并返回该子数组的长度。如果不存在这样的 子数组 ,返回 -1 。
子数组 是数组中 连续 的一部分。
示例 1:
输入:nums = [1], k = 1
输出:1
示例 2:
输入:nums = [1,2], k = 4
输出:-1
示例 3:
输入:nums = [2,-1,2], k = 3
输出:3
提示:
1 <= nums.length <= 105-105 <= nums[i] <= 1051 <= k <= 109
思路:
从nums 中和至少为 k 的 最短非空子数组,且子数组 是数组中 连续 的一部分,由此想到使用前缀和,
具体使用如
求出前缀和s后,如果是枚举所有的i>j,s[i]-s[j]>=k的从j到i子数组中的数组长度最小值会超时,优化如下:
优化一:
定义左边元素为j,右边元素为i
如果s[i]-s[j]已经大于k了,继续向右寻找的s[j]无论如何长度都会比目前i-j长,因此继续向右继续寻找没有意义,将左边元素s[j]出队
优化二:
如果s[i]<=s[j],意味从j到i为增加的为负,这时候继续向右遍历x,如果满足s[x]-s[j]>k,因为s[i]<=s[j],那么s[x]-s[i]也会>k,减去一个更小的数,因此左边j没有必要,可以出队,当完成两个优化后,将此时的右边i入队
具体代码如下
class Solution {
public:
int shortestSubarray(vector<int>& nums, int k) {
int n = nums.size();
vector<long> preSumArr(n + 1);
for (int i = 0; i < n; i++) {
preSumArr[i + 1] = preSumArr[i] + nums[i];
}
int res = n + 1;
deque<int> qu;
for (int i = 0; i <= n; i++) {
long curSum = preSumArr[i];
while (!qu.empty() && curSum - preSumArr[qu.front()] >= k) {
res = min(res, i - qu.front());
qu.pop_front();
}
while (!qu.empty() && preSumArr[qu.back()] >= curSum) {
qu.pop_back();
}
qu.push_back(i);
}
return res < n + 1 ? res : -1;
}
};
力扣打卡第五天
已知函数 signFunc(x) 将会根据 x 的正负返回特定值:
- 如果
x是正数,返回1。 - 如果
x是负数,返回-1。 - 如果
x是等于0,返回0。
给你一个整数数组 nums 。令 product 为数组 nums 中所有元素值的乘积。
返回 signFunc(product) 。
简单题:定义一个判断正负的,遍历数组元素,当为负取反,当为0返回,最后判断返回
class Solution {
public:
int arraySign(vector& nums) {
bool zheng =true;
for(int i=0;i 力扣打卡第六天
给定一个整数数组 arr,找到 min(b) 的总和,其中 b 的范围为 arr 的每个(连续)子数组。
由于答案可能很大,因此 返回答案模 10^9 + 7 。
示例 1:
输入:arr = [3,1,2,4]
输出:17
解释:
子数组为 [3],[1],[2],[4],[3,1],[1,2],[2,4],[3,1,2],[1,2,4],[3,1,2,4]。
最小值为 3,1,2,4,1,1,2,1,1,1,和为 17。
示例 2:
输入:arr = [11,81,94,43,3]
输出:444
提示:
1 <= arr.length <= 3 * 1041 <= arr[i] <= 3 * 104
思路
- 利用单调栈向左找到第一个比A[i]小的数A[left](遍历顺序为0->n-1),也就是A[i]辐射范围的左边界;
- 利用单调栈向右找到第一个比A[i]小的数A[right](遍历顺序为n-1->0),也就是A[i]辐射范围的右边界;
- 将每个元素的贡献值求和得到最终答案
class Solution {
const int MOD = 1e9 + 7;
public:
int sumSubarrayMins(vector<int> &arr) {
long ans = 0L;
arr.push_back(-1);
stack<int> st;
st.push(-1); // 哨兵
for (int r = 0; r < arr.size(); ++r) {
while (st.size() > 1 && arr[st.top()] >= arr[r]) {
int i = st.top();
st.pop();
ans += (long) arr[i] * (i - st.top()) * (r - i); // 累加贡献
}
st.push(r);
}
return ans % MOD;
}
};
力扣打卡第七天
给你一个数组 items ,其中 items[i] = [typei, colori, namei] ,描述第 i 件物品的类型、颜色以及名称。
另给你一条由两个字符串 ruleKey 和 ruleValue 表示的检索规则。
如果第 i 件物品能满足下述条件之一,则认为该物品与给定的检索规则 匹配 :
ruleKey == "type"且ruleValue == typei。ruleKey == "color"且ruleValue == colori。ruleKey == "name"且ruleValue == namei。
统计并返回 匹配检索规则的物品数量 。
示例 1:
输入:items = [["phone","blue","pixel"],["computer","silver","lenovo"],["phone","gold","iphone"]], ruleKey = "color", ruleValue = "silver"
输出:1
解释:只有一件物品匹配检索规则,这件物品是 ["computer","silver","lenovo"] 。
示例 2:
输入:items = [["phone","blue","pixel"],["computer","silver","phone"],["phone","gold","iphone"]], ruleKey = "type", ruleValue = "phone"
输出:2
解释:只有两件物品匹配检索规则,这两件物品分别是 ["phone","blue","pixel"] 和 ["phone","gold","iphone"] 。注意,["computer","silver","phone"] 未匹配检索规则。
提示:
1 <= items.length <= 1041 <= typei.length, colori.length, namei.length, ruleValue.length <= 10ruleKey等于"type"、"color"或"name"- 所有字符串仅由小写字母组成
思路:
先获取ruleKey的索引值index,随后在给定数组对应的位置开始遍历,满足条件加一
代码如下
class Solution {
public:
int countMatches(vector<vector<string>>& items, string ruleKey, string ruleValue) {
int k;
if(ruleKey == "type")
k=0;
else if(ruleKey == "color")
k=1;
else if(ruleKey == "name")
k=2;
int n=items.size();
int ans =0;
for(int i=0;i<n;i++){
if(items[i][k]==ruleValue)
ans++;
}
return ans;
}
};
力扣打卡第八天
给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。
返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。
示例 1:
输入:s = "a1b2"
输出:["a1b2", "a1B2", "A1b2", "A1B2"]
示例 2:
输入: s = "3z4"
输出: ["3z4","3Z4"]
思路如下:
同样的思路我们还可以采用回溯的思想,从左往右依次遍历每个字符,当搜索到字符串 s 的 第i个字符,对第i个字符开始判断
isalpha(s[pos]
如果 第 i 个字符为一个数字,则我们继续检测下一个字符;
如果 第 i 个字符为一个字母,我们将字符串中的第 i个字符改变大小写,往后继续搜索,完成改写形式的子状态搜索后,我们将 第 i 个字符进行恢复,继续往后搜索;
如果当前完成字符串搜索后,则表示当前的子状态已经搜索完成,该序列为全排列中的一个;
代码如下:
class Solution {
public:
void dfs(string &s,int pos,vector<string> &res){
while(pos<s.size()&&isdigit(s[pos])){
pos++;
}
if(pos == s.size()){
res.emplace_back(s);
return;
}
s[pos]^=32;
dfs(s,pos+1,res);
s[pos]^=32;
dfs(s,pos+1,res);
}
vector<string> letterCasePermutation(string s) {
vector<string> ans;
dfs(s,0,ans);
return ans;
}
};
力扣打卡第九天
神奇字符串 s 仅由 '1' 和 '2' 组成,并需要遵守下面的规则:
- 神奇字符串 s 的神奇之处在于,串联字符串中
'1'和'2'的连续出现次数可以生成该字符串。
s 的前几个元素是 s = "1221121221221121122……" 。如果将 s 中连续的若干 1 和 2 进行分组,可以得到 "1 22 11 2 1 22 1 22 11 2 11 22 ......" 。每组中 1 或者 2 的出现次数分别是 "1 2 2 1 1 2 1 2 2 1 2 2 ......" 。上面的出现次数正是 s 自身。
给你一个整数 n ,返回在神奇字符串 s 的前 n 个数字中 1 的数目。力扣打卡第九天
思路:
先构造s字符串,具体就是间隔填1或2,从第三个字符串开始填充,填多少个1或2由当前遍历到的s[i]值决定,
可以由1^3=2, 2^3=1,实现 1 和 2 之间转换效果,当数组长度大于n时结束构造,最后统计s字符串内有多少个1
因为最后一次可能构造会出现2个1添加到字符串末尾,因此统计时长度限定为n,避免催错误。
class Solution {
public:
int magicalString(int n) {
string s = "\1\2\2"; // 构造前三个字符
for (int i = 2; s.length() < n; ++i)
s += string(s[i], s.back() ^ 3); // 不断的在末尾拼接1或2,等号右边生成s[i]个1或2
return count(s.begin(), s.begin() + n, 1);
}
};
力扣打卡第十天
给你两个字符串数组 word1 和 word2 。如果两个数组表示的字符串相同,返回 true ;否则,返回 false 。
数组表示的字符串 是由数组中的所有元素 按顺序 连接形成的字符串。
示例 1:
输入:word1 = ["ab", "c"], word2 = ["a", "bc"]
输出:true
解释:
word1 表示的字符串为 "ab" + "c" -> "abc"
word2 表示的字符串为 "a" + "bc" -> "abc"
两个字符串相同,返回 true
示例 2:
输入:word1 = ["a", "cb"], word2 = ["ab", "c"]
输出:false
示例 3:
输入:word1 = ["abc", "d", "defg"], word2 = ["abcddefg"]
输出:true
思路:
将两个给定的字符串数组拼接起来,再比较,当拼接的字符串长度不等或者逐一比较时不匹配,返回false,都完成了返回true
代码如下:
class Solution {
public:
bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {
string s1,s2;
s1=s2="";
for(int i=0;i<word1.size();i++){
s1+=word1[i];
}
for(int i=0;i<word2.size();i++){
s2+=word2[i];
}
if(s1.size()!=s2.size())
return false;
for(int i=0;i<s1.size();i++){
if(s1[i]!=s2[i])
return false;
}
return true;
}
};
力扣打卡第十一天
给你一个数组 towers 和一个整数 radius 。
数组 towers 中包含一些网络信号塔,其中 towers[i] = [xi, yi, qi] 表示第 i 个网络信号塔的坐标是 (xi, yi) 且信号强度参数为 qi 。所有坐标都是在 X-Y 坐标系内的 整数 坐标。两个坐标之间的距离用 欧几里得距离 计算。
整数 radius 表示一个塔 能到达 的 最远距离 。如果一个坐标跟塔的距离在 radius 以内,那么该塔的信号可以到达该坐标。在这个范围以外信号会很微弱,所以 radius 以外的距离该塔是 不能到达的 。
如果第 i 个塔能到达 (x, y) ,那么该塔在此处的信号为 ⌊qi / (1 + d)⌋ ,其中 d 是塔跟此坐标的距离。一个坐标的 信号强度 是所有 能到达 该坐标的塔的信号强度之和。
请你返回数组 [cx, cy] ,表示 信号强度 最大的 整数 坐标点 (cx, cy) 。如果有多个坐标网络信号一样大,请你返回字典序最小的 非负 坐标。
注意:
-
坐标
(x1, y1)字典序比另一个坐标
(x2, y2)小,需满足以下条件之一:
- 要么
x1 < x2, - 要么
x1 == x2且y1 < y2。
- 要么
-
⌊val⌋表示小于等于val的最大整数(向下取整函数)。
示例 1:
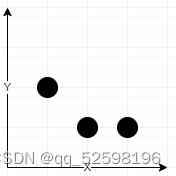
输入:towers = [[1,2,5],[2,1,7],[3,1,9]], radius = 2
输出:[2,1]
解释:
坐标 (2, 1) 信号强度之和为 13
- 塔 (2, 1) 强度参数为 7 ,在该点强度为 ⌊7 / (1 + sqrt(0)⌋ = ⌊7⌋ = 7
- 塔 (1, 2) 强度参数为 5 ,在该点强度为 ⌊5 / (1 + sqrt(2)⌋ = ⌊2.07⌋ = 2
- 塔 (3, 1) 强度参数为 9 ,在该点强度为 ⌊9 / (1 + sqrt(1)⌋ = ⌊4.5⌋ = 4
没有别的坐标有更大的信号强度。
示例 2:
输入:towers = [[23,11,21]], radius = 9
输出:[23,11]
解释:由于仅存在一座信号塔,所以塔的位置信号强度最大。
示例 3:
输入:towers = [[1,2,13],[2,1,7],[0,1,9]], radius = 2
输出:[1,2]
解释:坐标 (1, 2) 的信号强度最大。
思路:
暴力枚举从塔范围最小下标的到最大的下标,当满足塔能到达 的 最远距离则计算相应的强度,这里需注意坐标距离和塔能到达最远距离比较应该先平方,再开放,否则丢精度,和到累加信号强度值 ,返回最大强度值对应的下标。
代码如下
class Solution {
public:
vector<int> bestCoordinate(vector<vector<int>>& towers, int radius) {
int minx,miny,maxx,maxy;
minx=miny=0;
maxx=maxy=INT_MIN;
for(int i=0;i<towers.size();i++){
minx = min(minx,towers[i][0]);
maxx = max(maxx,towers[i][0]);
miny = min(miny,towers[i][1]);
maxy = max(maxy,towers[i][1]);
}
int maxq =0;
int q;
int xx,yy,qq;
int d;
int cx=minx,cy=miny;
int xinhaoq;
for(int tx=minx;tx<=maxx;tx++){
for(int ty=miny;ty<=maxy;ty++){
xinhaoq=0;
for(int k=0;k<towers.size();k++){
xx=towers[k][0];
yy=towers[k][1];
qq=towers[k][2];
d=((xx-tx)*(xx-tx)+(yy-ty)*(yy-ty));
if(d<=radius*radius){
//cout<<"manzu"<
xinhaoq+=float(qq/(1+sqrt(d)));
}
}
//cout<
if(xinhaoq>maxq){
cx=tx;
cy=ty;
maxq=xinhaoq;
}
}
}
return {cx,cy}; //return {cx,cy};
}
};
力扣打卡第十二天
给你一个字符串 sequence ,如果字符串 word 连续重复 k 次形成的字符串是 sequence 的一个子字符串,那么单词 word 的 重复值为 k 。单词 word 的 最****大重复值 是单词 word 在 sequence 中最大的重复值。如果 word 不是 sequence 的子串,那么重复值 k 为 0 。
给你一个字符串 sequence 和 word ,请你返回 最大重复值 k 。
示例 1:
输入:sequence = "ababc", word = "ab"
输出:2
解释:"abab" 是 "ababc" 的子字符串。
示例 2:
输入:sequence = "ababc", word = "ba"
输出:1
解释:"ba" 是 "ababc" 的子字符串,但 "baba" 不是 "ababc" 的子字符串。
示例 3:
输入:sequence = "ababc", word = "ac"
输出:0
解释:"ac" 不是 "ababc" 的子字符串。
思路
注意到字符串长度不超过 100,从大到小枚举 word 的重复次数 k,判断 word 重复该次数后是否是 sequence 的子串,是则直接返回当前的重复次数 k。
代码如下:
class Solution {
public:
int maxRepeating(string sequence, string word) {
int ans = 0;
string t = word;
int x = sequence.size() / word.size();
for (int k = 1; k <= x; ++k) {
if (sequence.find(t) != string::npos) {
ans = k;
}
t += word;
}
return ans;
}
};
力扣打卡第十三天
在一根无限长的数轴上,你站在0的位置。终点在target的位置。
你可以做一些数量的移动 numMoves :
- 每次你可以选择向左或向右移动。
- 第
i次移动(从i == 1开始,到i == numMoves),在选择的方向上走i步。
给定整数 target ,返回 到达目标所需的 最小 移动次数(即最小 numMoves ) 。
示例 1:
输入: target = 2
输出: 3
解释:
第一次移动,从 0 到 1 。
第二次移动,从 1 到 -1 。
第三次移动,从 -1 到 2 。
示例 2:
输入: target = 3
输出: 2
解释:
第一次移动,从 0 到 1 。
第二次移动,从 1 到 3 。
提示:
-109 <= target <= 109target != 0
思路:
走n步,
如果到达终点, 最小移动次数就是n,
如果越过了终点,如果越过的位置减目标位置为偶数,最小次数也是n,因为可以把其中的一步反向走,退回到n
如果越过了终点,如果越过的位置减目标位置为奇数,多走一步转换成上一种情况,
如果无法转换,则多走两步,必然为偶数,奇数再加上两个相邻数字(必定一偶一奇),即奇数+偶数+奇数,可以得到偶数
代码如下:
class Solution {
public:
int reachNumber(int target) {
target = abs(target);//终点可能为负数,取正数同解;
int s,n;//已累计步长和当前步长(移动次数)
s=n=0;
//当为到达终点或者越过终点距离不为奇数时继续添加
while(s<target||(s-target)%2){
s+=++n;
}
return n;
}
};
力扣打卡第十四天
给你一个以字符串形式表述的 布尔表达式(boolean) expression,返回该式的运算结果。
有效的表达式需遵循以下约定:
"t",运算结果为True"f",运算结果为False"!(expr)",运算过程为对内部表达式expr进行逻辑 非的运算(NOT)"&(expr1,expr2,...)",运算过程为对 2 个或以上内部表达式expr1, expr2, ...进行逻辑 与的运算(AND)"|(expr1,expr2,...)",运算过程为对 2 个或以上内部表达式expr1, expr2, ...进行逻辑 或的运算(OR)
示例 1:
输入:expression = "!(f)"
输出:true
示例 2:
输入:expression = "|(f,t)"
输出:true
示例 3:
输入:expression = "&(t,f)"
输出:false
示例 4:
输入:expression = "|(&(t,f,t),!(t))"
输出:false
思路如下:
使用栈,逐个遍历 expression 里面的每一个字符,如果:
-
字符是 , 那么跳过就好了,不需要往栈里面放。
-
字符是 ( 照样放进栈里面去,因为这个是用来标记嵌套的起始位置的。
-
字符是 ) 那么就把栈里面字符挨个弹出来放到新的栈中去,直到遇到了 ( 起始位置,此时新的栈中获取到的就是 () 里面的内容。然后再处理新栈中的表达式:
-
先取出来 () 外面的操作符 char operator = stack.pollLast()。
-
如果 operator == ! 那么说明新栈里面只会有一个字符,反转就好了。
-
如果 operator == & 或者 operator == | 将表达式串分解为几个小串,递归调用自身判断真假结果。
-
代码如下:
class Solution {
public:
bool parseBoolExpr(string expression) {
if(expression == "f") return false;
if(expression == "t") return true;
if(expression[0] == '!'){
expression.pop_back();
return !parseBoolExpr(expression.substr(2));
}
int i = 0; while(expression[i] != '(') i++;
int j = expression.size() - 1; while(expression[j] != ')') j--;
string ev;
int cnt = 0;
if(expression[0] == '&'){
for(int k = i + 1; k < j; ++k){
if(expression[k] == '(') cnt++;
else if(expression[k] == ')') cnt--;
if(expression[k] == ','){
if(cnt != 0) ev += expression[k];
else {
if(!parseBoolExpr(ev)) return false;
ev.clear();
}
}
else ev += expression[k];
}
if(!parseBoolExpr(ev)) return false;
return true;
}
else if(expression[0] == '|'){
for(int k = i + 1; k < j; ++k){
if(expression[k] == '(') cnt++;
else if(expression[k] == ')') cnt--;
if(expression[k] == ','){
if(cnt != 0) ev += expression[k];
else {
if(parseBoolExpr(ev)) return true;
ev.clear();
}
}
else ev += expression[k];
}
if(parseBoolExpr(ev)) return true;
return false;
}
// impossible
return false;
}
};
力扣打卡第十五天
请你设计一个可以解释字符串 command 的 Goal 解析器 。command 由 "G"、"()" 和/或 "(al)" 按某种顺序组成。Goal 解析器会将 "G" 解释为字符串 "G"、"()" 解释为字符串 "o" ,"(al)" 解释为字符串 "al" 。然后,按原顺序将经解释得到的字符串连接成一个字符串。
给你字符串 command ,返回 Goal 解析器 对 command 的解释结果。
示例 1:
输入:command = "G()(al)"
输出:"Goal"
解释:Goal 解析器解释命令的步骤如下所示:
G -> G
() -> o
(al) -> al
最后连接得到的结果是 "Goal"
示例 2:
输入:command = "G()()()()(al)"
输出:"Gooooal"
示例 3:
输入:command = "(al)G(al)()()G"
输出:"alGalooG"
提示:
1 <= command.length <= 100command由"G"、"()"和/或"(al)"按某种顺序组成
遍历字符串,将满足条件的字符对应转换拼装即可
代码如下:
class Solution {
public:
string interpret(string command) {
string res="";
for(int i=0;i<command.size();i++){
if(command[i]=='G')
res+='G';
if(command[i]=='('&&command[i+1]==')'){
res+='o';
i++;
continue;
}
if(command[i]=='('&&command[i+1]=='a'){
res+="al";
i+=3;
continue;
}
}
return res;
}
};
力扣打卡第十六天
我们有一些二维坐标,如 "(1, 3)" 或 "(2, 0.5)",然后我们移除所有逗号,小数点和空格,得到一个字符串S。返回所有可能的原始字符串到一个列表中。
原始的坐标表示法不会存在多余的零,所以不会出现类似于"00", “0.0”, “0.00”, “1.0”, “001”, "00.01"或一些其他更小的数来表示坐标。此外,一个小数点前至少存在一个数,所以也不会出现“.1”形式的数字。
最后返回的列表可以是任意顺序的。而且注意返回的两个数字中间(逗号之后)都有一个空格。
示例 1:
输入: "(123)"
输出: ["(1, 23)", "(12, 3)", "(1.2, 3)", "(1, 2.3)"]
示例 2:
输入: "(00011)"
输出: ["(0.001, 1)", "(0, 0.011)"]
解释:
0.0, 00, 0001 或 00.01 是不被允许的。
示例 3:
输入: "(0123)"
输出: ["(0, 123)", "(0, 12.3)", "(0, 1.23)", "(0.1, 23)", "(0.1, 2.3)", "(0.12, 3)"]
示例 4:
输入: "(100)"
输出: [(10, 0)]
解释:
1.0 是不被允许的。
提示:
4 <= S.length <= 12.S[0]= “(”,S[S.length - 1]= “)”, 且字符串S中的其他元素都是数字。
主要是如何确认小数,即把小数的逗号位置确认,判断方法如下:
- 字符串开头不为0,整体可以作为数字分,小数可以放在任何位置
- 字符串末尾不为0,小数点可以放在第一个数字的后面
注意返回的两个数字中间(逗号之后)都有一个空格。
代码如下:
class Solution {
public:
vector<string>gets(string s){
vector<string>ans;
if(s == "0") return vector<string> {s};
if(s[0] !='0') ans.push_back(s);
if(s[s.size()-1] !='0'){
for(int i=1;i<s.size();i++){
if(s[0]=='0'&&i!=1) continue;
string s1 = s.substr(0,i),s2=s.substr(i,s.size()-1);
string temp = s1 + "." + s2;
ans.push_back(temp);
}
}
return ans;
}
vector<string> ambiguousCoordinates(string s) {
s = s.substr(1,s.size()-2);
vector<string>ans;
for(int i=1;i<s.size();i++){
vector<string>s1 = gets(s.substr(0,i));
vector<string>s2 = gets(s.substr(i,s.size()-1));
for(int ci=0;ci<s1.size();ci++){
for(int cj=0;cj<s2.size();cj++){
string temp = "(" + s1[ci] + ", " + s2[cj] + ")";
ans.push_back(temp);
}
}
}
return ans;
}
};
力扣打卡第十七天
给你一个由不同字符组成的字符串 allowed 和一个字符串数组 words 。如果一个字符串的每一个字符都在 allowed 中,就称这个字符串是 一致字符串 。
请你返回 words 数组中 一致字符串 的数目。
示例 1:
输入:allowed = "ab", words = ["ad","bd","aaab","baa","badab"]
输出:2
解释:字符串 "aaab" 和 "baa" 都是一致字符串,因为它们只包含字符 'a' 和 'b' 。
示例 2:
输入:allowed = "abc", words = ["a","b","c","ab","ac","bc","abc"]
输出:7
解释:所有字符串都是一致的。
示例 3:
输入:allowed = "cad", words = ["cc","acd","b","ba","bac","bad","ac","d"]
输出:4
解释:字符串 "cc","acd","ac" 和 "d" 是一致字符串。
提示:
1 <= words.length <= 1041 <= allowed.length <= 261 <= words[i].length <= 10allowed中的字符 互不相同 。words[i]和allowed只包含小写英文字母。
思路:
定义一个数组,标记allowed出现过的下标数组,下标使用 allowed[i] - ‘a’ ,随后用比较标记位判断是否出现。
代码如下:
class Solution {
public:
int countConsistentStrings(string allowed, vector<string>& words) {
int judge[26]={0};
for(int i=0;i<allowed.size();i++){
judge[allowed[i]-'a']=1;
}
int ans=0;
for(int i=0;i<words.size();i++){
bool flag =true;
string sj = words[i];
for(int j=0;j<sj.size();j++){
if(judge[sj[j]-'a']==0){
flag =false;
continue;
}
}
if(flag)
ans++;
}
return ans;
}
};
力扣打卡第十八天
在一个 n x n 的矩阵 grid 中,除了在数组 mines 中给出的元素为 0,其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0
返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志,返回 0 。
提示:
1 <= n <= 5001 <= mines.length <= 50000 <= xi, yi < n- 每一对
(xi, yi)都 不重复
思路如下:
暴力遍历,即遍历扫描每一个点,并且记录能够延伸的长度。
1.先创建能遍历的数组grid,将给定0添加到数组中,1为能遍历的点。
2.双层for循环遍历每一个点,并且上下左右去延伸,然后拿到最小的延伸,因为是轴对称图形,最小才能让他们轴对称,类似木桶理论,最短那块板决定了这个桶能装多少水的感觉。
3.存储结果,每次都与上一个点作比较,找到最大的。
同时剪枝优化:
每次在开始延伸前,判断一下坐标点到四个方向边界的最小距离,这决定了加号的阶数上限,当上限都不大于当前res时,就可以跳过了
代码如下:
class Solution {
public:
int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
vector<vector<int>> grid(n, vector<int>(n, 1));//创建二维数组全为1
for (auto mine : mines) {
grid[mine[0]][mine[1]] = 0;
}
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
int curMin = min(min(i + 1, j + 1), min(n - i, n - j));
if (curMin <= res) continue;//判断该坐标到四个方向边界的距离,若不大于当前的res,就跳过
int up = 0, down = 0, left = 0, right = 0;
while (grid[i][j] == 1 && i - up >= 0 && grid[i - up][j] == 1) up++;
while (grid[i][j] == 1 && i + down < n && grid[i + down][j] == 1) down++;
while (grid[i][j] == 1 && j - left >= 0 && grid[i][j - left] == 1) left++;
while (grid[i][j] == 1 && j + right < n && grid[i][j + right] == 1) right++;
curMin = min(min(up, down), min(left, right));
res = max(res, curMin);
}
}
return res;
}
};
力扣打卡第十九天
给定一个二维网格 grid ,其中:
- ‘.’ 代表一个空房间
- ‘#’ 代表一堵
- ‘@’ 是起点
- 小写字母代表钥匙
- 大写字母代表锁
我们从起点开始出发,一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走,也无法穿过一堵墙。如果途经一个钥匙,我们就把它捡起来。除非我们手里有对应的钥匙,否则无法通过锁。
假设 k 为 钥匙/锁 的个数,且满足 1 <= k <= 6,字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之,每个锁有唯一对应的钥匙,每个钥匙也有唯一对应的锁。另外,代表钥匙和锁的字母互为大小写并按字母顺序排列。
返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙,返回 -1 。
示例 1:
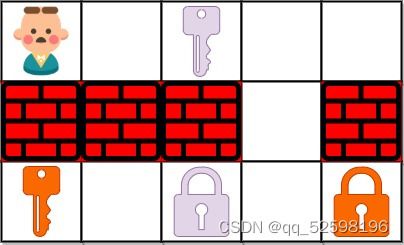
输入:grid = ["@.a.#","###.#","b.A.B"]
输出:8
解释:目标是获得所有钥匙,而不是打开所有锁。
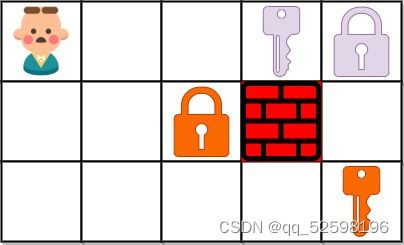
输入:grid = ["@..aA","..B#.","....b"]
输出:6
示例 3:
输入: grid = ["@Aa"]
输出: -1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]只含有'.','#','@','a'-``'f``'以及'A'-'F'- 钥匙的数目范围是
[1, 6] - 每个钥匙都对应一个 不同 的字母
- 每个钥匙正好打开一个对应的锁
思路:
搜索最短路径,首先应该想到BFS,而本题的难点在于收集钥匙和开锁,这意味着访问数组visited不能简单地使用坐标来表示了,还应该考虑到持有钥匙的情况。实现来讲,使用广度优先搜索处理各种情况(墙、钥匙、锁),并使用二进制数位来表示钥匙的持有情况。
代码如下:
class Solution {
public:
vector<vector<int>> dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int shortestPathAllKeys(vector<string>& grid) {
int m = grid.size(), n = grid[0].size();
int count = 0; //钥匙个数
int si = 0, sj = 0; //起点位置
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++) {
if(grid[i][j] >= 'a' && grid[i][j] <= 'z')
count++;
else if(grid[i][j] == '@') {
si = i;
sj = j;
}
}
queue<tuple<int, int, int>> q; //BFS
q.push({si, sj, 0}); //当前位置与当前钥匙状态,钥匙状态用二进制数表示
vector<vector<vector<int>>> visited(m, vector<vector<int>>(n, vector<int>(1<<count, 0)));
//visited[i][j][state]表示在位置(i, j)拥有钥匙状态state时是否已经访问
visited[si][sj][0] = 1;
int ans = 0;
while(!q.empty()) {
int size = q.size();
for(int k = 0; k < size; k++) {
auto [i, j, state] = q.front();
q.pop();
if(__builtin_popcount(state) == count)
return ans; //找到了所有的钥匙
for(vector<int> & dir : dirs) {
int x = i + dir[0], y = j + dir[1];
if(x >= 0 && x < m && y >= 0 && y < n) {
char c = grid[x][y];
if(c == '#' || (c >= 'A' && c <= 'Z' && (state>>(c - 'A') & 1) == 0))
continue; //遇到墙,或者遇到锁而没有对应钥匙,跳过
int nstate = state;
if(c >= 'a' && c <= 'z')
nstate |= 1<<(c - 'a'); //获得钥匙,更新状态
if(visited[x][y][nstate] == 0) { //该状态未被访问,入队
visited[x][y][nstate] = 1;
q.push({x, y, nstate});
}
}
}
}
ans++; //步数加一
}
return -1;
}
};
力扣打卡第二十天
给你一个偶数长度的字符串 s 。将其拆分成长度相同的两半,前一半为 a ,后一半为 b 。
两个字符串 相似 的前提是它们都含有相同数目的元音('a','e','i','o','u','A','E','I','O','U')。注意,s 可能同时含有大写和小写字母。
如果 a 和 b 相似,返回 true ;否则,返回 false 。
示例 1:
输入:s = "book"
输出:true
解释:a = "bo" 且 b = "ok" 。a 中有 1 个元音,b 也有 1 个元音。所以,a 和 b 相似。
示例 2:
输入:s = "textbook"
输出:false
解释:a = "text" 且 b = "book" 。a 中有 1 个元音,b 中有 2 个元音。因此,a 和 b 不相似。
注意,元音 o 在 b 中出现两次,记为 2 个。
思路:
定义一个ans,记录前半段的元音个数,判断后半段的元音,如果减到0,则相似true,否则返回不相似false
代码如下:
class Solution {
public:
bool halvesAreAlike(string s) {
int n =s.size();
int ans=0;
int i=0;
for(;i<n/2;i++)
{
if(s[i]=='a'||s[i]=='e'||s[i]=='i'||s[i]=='o'||s[i]=='u'||s[i]=='A'||s[i]=='E'||s[i]=='I'||s[i]=='O'||s[i]=='U')
ans++;
}
for(;i<n;i++)
{
if(s[i]=='a'||s[i]=='e'||s[i]=='i'||s[i]=='o'||s[i]=='u'||s[i]=='A'||s[i]=='E'||s[i]=='I'||s[i]=='O'||s[i]=='U')
ans--;
}
if(ans)
return false;
else
return true;
}
};
力扣打卡第二十一天
有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
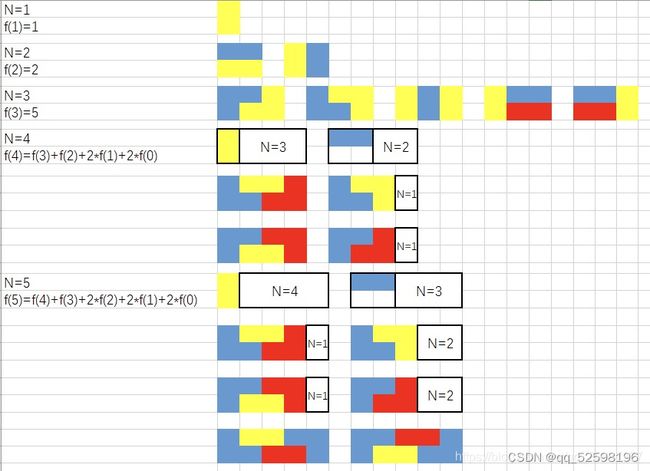
示例 1:
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:
输入: n = 1
输出: 1
思路:
找规律得到递推公式 f(N)=2*f(N-1)+f(N-3)
代码如下
class Solution {
public:
int numTilings(int N) {
int mod=1000000007;
vector<int> dp(N+3,0);
dp[1]=1;
dp[2]=2;
dp[3]=5;
for(int i=4;i<=N;i++){
dp[i]=(2*dp[i-1]%mod+dp[i-3])%mod;
}
return dp[N];
}
};