代码随想录刷LeetCode | 二叉树刷题回顾02

前沿：撰写博客的目的是为了再刷时回顾和进一步完善，其次才是以教为学，所以如果有些博客写的较简陋，是为了保持进度不得已而为之，还请大家多多见谅。

预：看到题目后的思路和实现的代码。

见：参考答案展示。

感思：对比答案后的思考，与之前做过的题目是否有关联。

行：

（1）对于没做出来的题目，阅读答案后重新做一遍；

（2）下次做题可以尝试改善的方向；

（3）有助于理解的相关的题目

优先级：做题＞学习&总结＞默写回顾＞做题数量

题目回顾

1.二叉树的层序遍历

题目链接：102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。

（即逐层地，从左到右访问所有节点）。

BFS深度优先遍历：DeQueue队列（先进先出）-迭代法

DeQueque que = new LinkedList() ;

que.offerpoll(root);

while终止条件:队列不为空

• List itemList = new ArrayList();嵌套List要每层新建List分别存储；
• TreeNode tempNode = que.pollpop();队列弹出当前节点，并赋予临时变量；
• 再将当前节点值存入result中。
• 读取队列此时长度，即每层需要遍历的次数：int len = que.size()→while(len-- > 0)
  • TreeNode tempNode = que.pollpop();队列弹出当前节点，并赋予临时变量；
  • 依次判断是否存在左、右节点，存在则存入队列中。

二刷没做出来反思

做题时10分钟没有思路跳，看完题解后仍不能直接实现出来。

队列+两层嵌套while-迭代法实现：

以为一层len便能够实现，发现需要找到每层截止点，想用if判断找到，但失败了。

与组合总和III一样发现实现不了时，没有想从其他地方来解决问题；

像使用两层while循环便能分割层，而终止条件复杂无法实现时，则选择再for循环中多筛选解决问题。

DFS深度优先遍历-递归-前序优先遍历

1.递归函数类型值和返回值：deep记录当前遍历的层数，保证找到相关层。

public void checkFun01(TreeNode node, Integer deep)

2.单层递归逻辑：

        if (resList.size() < deep) {
            //当层级增加时，list的Item也增加，利用list的索引值进行层级界定
            List item = new ArrayList();
            resList.add(item);
        }
        resList.get(deep - 1).add(node.val);

        checkFun01(node.left, deep);
        checkFun01(node.right, deep);

3.递归终止条件：

if (node == null) return;

参考来源：代码随想录：二叉树的层序遍历

2.翻转二叉树

题目链接：226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

BFS深度优先遍历：DeQueue队列（先进先出）-迭代法

ArrayDeque deque = new ArrayDeque() ;

deque.offerpoll(root);

while终止条件:队列不为空

• List itemList = new ArrayList();嵌套List要每层新建List分别存储；
• 再将当前节点值存入result中。
• 读取队列此时长度，即每层需要遍历的次数：int len = que.size()→while(len-- > 0)
  • TreeNode tempNode = que.pollpop();队列弹出当前节点，并赋予临时变量；
  • 创建临时变量，将左右子节点转换；
  • 依次判断是否存在左、右节点，存在则存入队列中。

DFS深度优先遍历-递归：前后序遍历都可以

1.递归函数类型值和返回值：以题目定义的为递归函数,无需自行再定义！

2.单层递归逻辑：invertTree(root.left); invertTree(root.right); 创建临时变量，将左右子节点转换；

3.递归终止条件：当节点为空时终止

3. 对称二叉树

题目链接：101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

DFS深度优先遍历-递归："后"序遍历

1.递归函数类型值和返回值：以题目定义的为递归函数,无需自行再定义！

 private boolean compare(TreeNode left, TreeNode right) {
                    ...
        return compareOutside && compareInside;
}

2.单层递归逻辑：

• 外边对称判断:boolean compareOutside = compare(left.left,right.right);
• 内边对称判断:boolean compareInside = compare(left.right,right.left);

3.递归终止条件：当左右节都为空or都不为空值为True；

class Solution {
    public boolean isSymmetric(TreeNode root) {
        //递归-分别判断外层和内层相同
        if (root == NULL) return true;
        return compare(root.left,root.right);

    }
    boolean compare(TreeNode left,TreeNode right){
        if(left == null && right == null){
            return true;
        }else if(left == null || right == null || left.val != right.val){
            return false;
        }
        boolean outside = compare(left.left,right.right);
        boolean inside = compare(left.right,right.left);
        return outside && inside;
    }
}

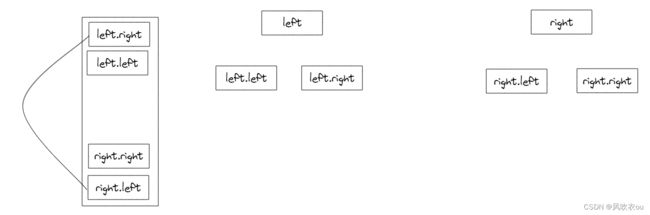
BFS广度优先遍历-迭代：双端队列Deque

迭代-双端队列法

    public boolean isSymmetric2(TreeNode root) {
        Deque deque = new LinkedList<>();
        deque.offerFirst(root.left);
        deque.offerLast(root.right);
        while (!deque.isEmpty()) {
            TreeNode leftNode = deque.pollFirst();
            TreeNode rightNode = deque.pollLast();
            if (leftNode == null && rightNode == null) {
                continue;
            }
            if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
                return false;
            }
            deque.offerFirst(leftNode.left);
            deque.offerFirst(leftNode.right);
            deque.offerLast(rightNode.right);
            deque.offerLast(rightNode.left);
        }
        return true;
    }

迭代-普通栈法

            // 这里顺序与使用Deque不同
            deque.offer(leftNode.left);
            deque.offer(rightNode.right);
            deque.offer(leftNode.right);
            deque.offer(rightNode.left);

参考来源：代码随想录：对称二叉树

小结：

1.当单层递归逻辑想不通时，反过去质疑是否是递归函数类型值和返回值没有写好？

• 尤其是这题的返回值不是单纯某个值，而是一个并行判断语句。

相关知识点

 Stack与Queue、Deque关联：

Stack属于栈，而Queue和Deque都属于队列，但后者属于两端队列，即前后都能添加删除。

stack.pop()与que.poll()都是是取出（移除）LinkedList的第一个元素；

Queue——单端队列；Deque——双端队列；

	Stack	Queue	Deque
增	push	add	addFirst/addLast
删	pop	poll/remove	pollFirst(remove)/pollLast
查	peek	peek	getFirst/getLast

Stack栈结构每次都需要压入新的元素，所以使用push推/按进去；而Queue队列则是正常加进去，所以使用add，而Deque是两端加入，则在基础上使用addFirst/addLast。

Stack栈结构每次删除时，则是要弹出栈顶元素，pop就是弹出、发出爆炸声的意思；而Queue队列则是相当于绳子按照次序剪掉最前面的，而poll则有剪短的意思。

• 其中poll和remove的区别在于，取出值为空值，poll返回null，而remove返回false。

LinkedList与ArrayList关联：

Java LinkedList（链表） 类似于 ArrayList，是一种常用的数据容器。

与 ArrayList 相比，LinkedList 的增加和删除的操作效率更高，而查找和修改的操作效率较低。

以下情况使用 ArrayList :

• 频繁访问列表中的某一个元素。
• 只需要在列表末尾进行添加和删除元素操作。

以下情况使用 LinkedList :

• 你需要通过循环迭代来访问列表中的某些元素。
• 需要频繁的在列表开头、中间、末尾等位置进行添加和删除元素操作。

参考来源：

Java LinkedList | 菜鸟教程 (runoob.com)

总结

DFS深度优先遍历-递归+int index→层序遍历

BFS广度优先遍历=while+队列实现