python形态学滤波：腐蚀、膨胀、开、闭运算

最基础的形态学操作有四个，分别是腐蚀、膨胀、开计算和闭计算，`scipy.ndimage分别实现了二值数组和灰度数组的这四种运算

二值	灰度
binary_erosion	grey_erosion	腐蚀
binary_dilation	grey_dilation	膨胀
binary_closing	grey_closing	闭(先膨胀后腐蚀)
binary_opening	grey_opening	开(先腐蚀后膨胀)

二值形态学

所谓腐蚀，用数学符号表示为

$$A\ominus B=\{(i,j)|B_{ij}\subseteq A\}$$

其中$B_{ij}$表示当$B$的原点在$(i,j)$处时，B中所有为1的值的集合。

这个式子的意思是，用结构B腐蚀A，当B的原点平移到图像A的像元$(i,j)$时，若B完全被二者的重叠区域所包围，则赋值为1，否则赋值为0。更直观的例子是，如果B中为1的元素位置上，对应的A的像素值也都为1，则$(i,j)$处为1。

膨胀则与之相反，可表示为

$$A\oplus B=\{(i,j)|B_{ij}\cup A\ne \varnothing \}$$

换言之，只要$B$和$A$的重叠区域不是空集，那么$(i,j)$点就置为1。

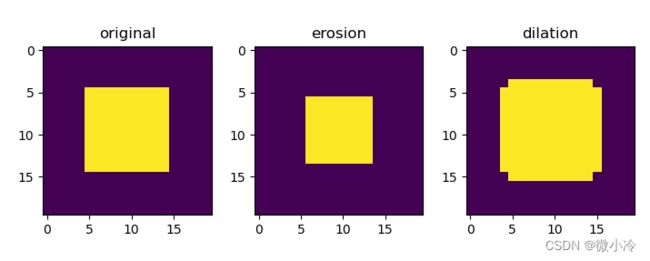
举个例子如下

import numpy as np
import matplotlib.pyplot as plt
import scipy.ndimage as sn

x = np.zeros([20,20])
x[5:15, 5:15] = 1
x_ero = sn.binary_erosion(x)
x_dil = sn.binary_dilation(x)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.imshow(x)
plt.title("original")
ax = fig.add_subplot(1,3,2)
ax.imshow(x_ero)
plt.title("erosion")
ax = fig.add_subplot(1,3,3)
ax.imshow(x_dil)
plt.title("dilation")
plt.show()

效果如下

开运算是先腐蚀后膨胀；闭运算是先膨胀后腐蚀，示例如下

x = np.zeros([20,20])
x[5:15, 5:15] = 1
x[10:12,10:12] = 0
x[2:4, 2:4] = 1

x_open = sn.binary_opening(x)
x_close = sn.binary_closing(x)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.imshow(x)
plt.title("original")
ax = fig.add_subplot(1,3,2)
ax.imshow(x_open)
plt.title("opening")
ax = fig.add_subplot(1,3,3)
ax.imshow(x_close)
plt.title("closing")
plt.show()

效果如下，可见开运算会去除孤立的1，闭运算会去除孤立的0。

灰度形态学

灰度图像的腐蚀、膨胀以及开闭运算，是其二值形势下的一个扩展，采用了类似卷积的逻辑，下面直接从scipy中调取楼梯图片，并依次做腐蚀、膨胀以及开闭操作。

from scipy.misc import ascent
img = ascent()

funcs = {
    "original": lambda x, tmp:x,
    "erosion" : sn.grey_erosion,
    "dilation" : sn.grey_dilation,
    "opening" : sn.grey_opening,
    "closing" : sn.grey_closing
}

fig = plt.figure()
for i, key in enumerate(funcs):
    ax = fig.add_subplot(2,3,i+1)
    plt.imshow(funcs[key](img, (10,10)), cmap=plt.cm.gray)
    plt.title(key)

plt.show()

效果如下

参数列表

二值函数和灰度函数的参数并不相同，下面以closing运算为例，二值和灰度函数的所有参数，除了输入input之外，二者共有的参数有

• structure 为数组类型，表示构造元素，可以理解为是卷积模板
• output 与输入相同维度的数组，可以存下结果
• orgin 过滤器设置，默认为0

二值形态学滤波的其他参数如下

binary_closing(input, iterations=1, mask=None, border_value=0, brute_force=False)

其中

• iterations 执行次数
• mask 掩模数组，为bool类型的数组，对应False的位置将不会改变
• border_value 边缘处的值
• brute_force 如果为False，则只有上次迭代中发生变化的值才会更新

grey_closing(input, size=None, footprint=None, mode='reflect', cval=0.0)

• size 为滤波模板
• mode 可选reflect,constant,nearest,mirror, wrap，边缘填充方式
• cval 边缘填充值