算法刷题总结 (六) 前缀树 | 字典树 | 单词查找树
算法总结6 前缀树 | 字典树 | 单词查找树
- 一、理解字典树算法
-
- 1.1、字面含义
- 1.2、字典树的由来
- 1.3、单词在字典树中如何存储
- 1.4、字典树的结构
- 二、经典问题
-
- 208. 实现 Trie (前缀树)
- 648. 单词替换
- 211. 添加与搜索单词 - 数据结构设计 (增加DFS)
- 677. 键值映射(节点属性,前缀数)
- 676. 实现一个魔法字典 (DFS)
- 820.单词的压缩编码
- 其他相似题型
一、理解字典树算法
1.1、字面含义
字典树分为字典和树。
“字典”很好理解,字典是Python里的一种数据结构,它算是一种哈希表,查找的速度非常快,所以查找用它来代替list等结构。它的某种写法例子如下:
dict_example = {'fruits':['apple', 'orange'], 'language':['English', 'Chinese']}
“树”也很好理解,是算法里的一种数据结构,或者理解为机器学习里的决策树。我们可以画一个倒着的树去模拟它,也可以使用if和else去以代码的形式展现它:
[salary_year]
/ \
>300000 <300000
/ \
"可以贷款" [estate]
/ \
"有" "无"
/ \
"可以贷款" [son_or_daug]
/ \
"有" "无"
/ \
"可以贷款" "不能贷款"
if salary_year > 300000:
return "可以贷款"
else
if estate:
return "可以贷款"
else
if son_or_daug == True:
return "可以贷款"
else
return "不能贷款"
... ...
那么如何理解字典树呢?字典+树,就是将树以字典的形式表示,例子如下:
dict_example = {"salary_year":
{"可以贷款":{},
"estate":
{"可以贷款":{},
"son_or_daug":
{"可以贷款":{},
"不能贷款":{}
}
}
}
}
1.2、字典树的由来
字典树英文表示为:trie ,它来自于 retrieval 的中间部分。在wiki百科中,trie表示tree的意思,它属于多叉树结构,是一种哈希树的变种,典型应用场景是统计、保存大量的字符串,经常被搜索引擎系统用于文本词频统计。它的优点是利用字符串的公共前缀来减少查找时间,最大限度的减少无谓字符串的比较和存储空间。
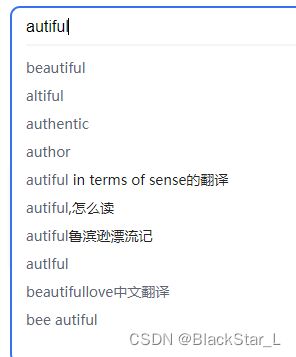
在搜索引擎中,当我们随便输入一个数,这里我输入一个不存在的单词,即beautiful的右半边autiful,下面显示了模糊匹配,它的前缀补齐beautiful,以及后缀补齐beautifullove。前两者对应了字典树中的前缀树和后缀树。
字典树也一般指的是前缀树,并且后面的案例也主要以前缀树为例子。
1.3、单词在字典树中如何存储
单词如何在字典树中进行存储?
我们可以像前面 字典+树 的形式那样,把单个字母当成一个节点存储在树形字典里。
但是,在很多文章中,字典树的节点的存储又不一样,有的是按照前面说的,节点直接存储字母,比如:一文搞懂字典树!
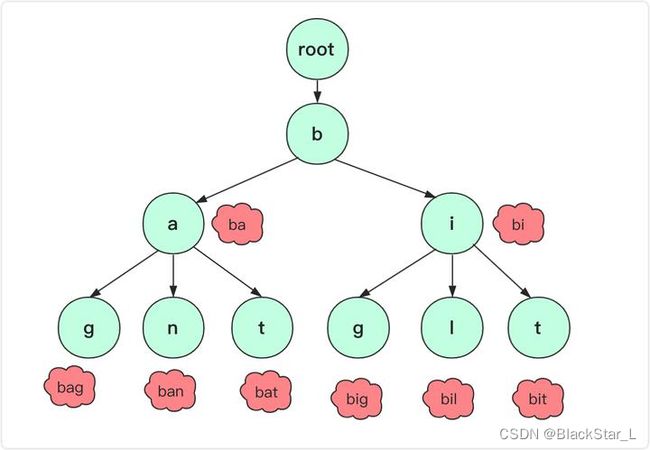
而有的文章说节点存储的是其他变量属性,而字母是存储在路径中。在官方的百度百科 字典树中写的是第二种,所以我们以第二种写法去理解字典树。

1.4、字典树的结构
字典树是一个由“路径”和“节点”组成多叉树结构。由根节点出发,按照存储字符串的每个字符,创建对应字符路径。由“路径”记载字符串中的字符,由节点记载经过的字符数以及结尾字符结尾数,例如一个简单的字符串集合:[them, zip, team, the, app, that]
- 根结点无实际意义
- 每一个节点数据域存储一个字符
- 每个节点中的控制域可以自定义,如 isWord(是否是单词),count(该前缀出现的次数)等,需实际问题实际分析需要什么。
class TrieNode:
def __init__(self):
self.count = 0 # 表示以该处节点构成的串的个数
self.preCount = 0 # 表示以该处节点构成的前缀的字串的个数
self.children = {}
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
node = self.root
for ch in word:
if ch not in node.children:
node.children[ch] = TrieNode()
node = node.children[ch]
node.preCount += 1
node.count += 1
def search(self, word):
node = self.root
for ch in word:
if ch not in node.children:
return False
node = node.children[ch]
return node.count > 0
def startsWith(self, prefix):
node = self.root
for ch in prefix:
if ch not in node.children:
return False
node = node.children[ch]
return node.preCount > 0
二、经典问题
208. 实现 Trie (前缀树)
class Trie:
def __init__(self):
self.root = {}
def insert(self, word: str) -> None:
root = self.root
for w in word:
if w not in root:
root[w]={}
root = root[w]
# 每个单词,设置一个结尾,说明该单词存在
# 比如存了pieapple,但没存pie,搜索pie时,虽然能搜到但实际上该单词不存在
root["#"]='#'
# 这里任意符号都可以,只要不是字母,并且能够区分出单词的结尾
# 比如 root['end']={}
def search(self, word: str) -> bool:
root = self.root
for w in word:
if w not in root:
return False
root = root[w]
# 说明到了结尾
if '#' in root:
return True
return False
def startsWith(self, prefix: str) -> bool:
root = self.root
for pre in prefix:
if pre not in root:
return False
root = root[pre]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
648. 单词替换
648. 单词替换
这里没有使用类结构,直接面向过程
class Solution:
def replaceWords(self, dictionary: List[str], sentence: str) -> str:
root = {}
for word in dictionary:
cur = root
for c in word:
if c not in cur:
cur[c]={}
cur = cur[c]
cur['#']='#'
words = sentence.split()
for ind, word in enumerate(words):
cur = root
for ind2, c in enumerate(word):
if '#' in cur:
words[ind] = word[:ind2]
break
if c not in cur:
break
cur = cur[c]
return ' '.join(words)
面向对象编程:
class Trie:
def __init__(self):
self.root = {}
def insert(self, word):
root = self.root
for c in word:
if c not in root:
root[c]={}
root = root[c]
root['#'] = '#'
def query(self, word):
root = self.root
for ind, c in enumerate(word):
if '#' in root:
return word[:ind]
if c not in root:
return False
root = root[c]
class Solution:
def replaceWords(self, dictionary: List[str], sentence: str) -> str:
trie = Trie()
for word in dictionary:
trie.insert(word)
words = sentence.split()
for ind, word in enumerate(words):
res = trie.query(word)
if res:
words[ind]=res
return ' '.join(words)
哈希集合解法(复杂度相对高):
class Solution:
def replaceWords(self, dictionary: List[str], sentence: str) -> str:
dSet = set(dictionary)
words = sentence.split()
for ind, word in enumerate(words):
for j in range(1, len(words)+1):
if word[:j] in dSet:
words[ind] = word[:j]
break
return ' '.join(words)
211. 添加与搜索单词 - 数据结构设计 (增加DFS)
211. 添加与搜索单词 - 数据结构设计
与前面的题目大致类似,但是,这里单词中有"."来表示所有可能的字母,需要深度优先搜索来迭代进行判断。
class WordDictionary:
def __init__(self):
self.root = {}
def addWord(self, word: str) -> None:
root = self.root
for w in word:
if w not in root:
root[w] = {}
root = root[w]
root['#'] = '#'
def search(self, word: str) -> bool:
def dfs(ind, node):
# 索引和单词长度相等时表示搜索完了
if ind==len(word):
# 搜索完后如果是结尾标识"#",则能找到这个单词,否则不能
if '#' in node:
return True
else:
return False
ch = word[ind]
# 遍历到单词的 '.'
if ch=='.':
# 选择所有可替换的字母,注意不能为'#'
for c in node:
if c!='#' and dfs(ind+1, node[c]):
return True
# 遍历到单词其他字母
else:
if ch in node and dfs(ind+1, node[ch]):
return True
return False
return dfs(0, self.root)
# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)
参考官方解题官方: 添加与搜索单词 - 数据结构设计
677. 键值映射(节点属性,前缀数)
677. 键值映射
这题因为有了节点属性,相同单词前缀的value总值,那么我们需要不同于前面,必须创建一个Trie节点类,去额外存储这个属性,每个节点都包含值,并且在遍历的时候,值也跟着更新。
class Trie:
def __init__(self):
self.val = 0
# self.end = False
self.next = {}
class MapSum:
def __init__(self):
# 因为节点有属性,所以不再直接 self.root = {}
# 而是创建一个Trie节点,不仅存储self.next = {}字典树
# 并且存储self.val前缀值
self.root = Trie()
# 用来记录key-value
self.map = {}
def insert(self, key: str, val: int) -> None:
delta = val
# 相同key,之前累加过了,则增加变化量
if key in self.map:
delta = delta-self.map[key]
self.map[key]=val
root = self.root
for w in key:
if w not in root.next:
root.next[w]=Trie()
root = root.next[w]
# 不同单词相同前缀累加值,注意前面相同key的情况
root.val += delta
# root.end=True
def sum(self, prefix: str) -> int:
root =self.root
for p in prefix:
if p not in root.next:
return 0
root = root.next[p]
return root.val
# Your MapSum object will be instantiated and called as such:
# obj = MapSum()
# obj.insert(key,val)
# param_2 = obj.sum(prefix)
676. 实现一个魔法字典 (DFS)
676. 实现一个魔法字典
深度优先搜索每一个字符,设置标记是否改变,并且只能改变一次。
class MagicDictionary:
def __init__(self):
self.root = {}
def buildDict(self, dictionary: List[str]) -> None:
for word in dictionary:
root = self.root
for c in word:
if c not in root:
root[c]={}
root = root[c]
root['#']={}
# print(self.root)
def search(self, searchWord: str) -> bool:
def dfs(node, ind, modify):
if ind==len(searchWord):
if '#' in node and modify:
return True
return False
ch = searchWord[ind]
if ch in node:
if dfs(node[ch], ind+1, modify):
return True
if not modify:
for cnext in node:
if ch!=cnext:
if dfs(node[cnext], ind+1, True):
return True
return False
return dfs(self.root, 0, False)
# Your MagicDictionary object will be instantiated and called as such:
# obj = MagicDictionary()
# obj.buildDict(dictionary)
# param_2 = obj.search(searchWord)
820.单词的压缩编码
820.单词的压缩编码
class Trie:
def __init__(self):
self.count = 0
self.next = {}
class Solution:
def minimumLengthEncoding(self, words: List[str]) -> int:
root = Trie()
for word in words:
cur = root
for ind, c in enumerate(word[::-1]):
if c not in cur.next:
cur.next[c]=Trie()
cur = cur.next[c]
cur.count = ind+1
res = []
def dfs(node):
if not node.next:
res.append(node.count)
else:
for c in node.next:
dfs(node.next[c])
dfs(root)
return sum(res)+len(res)
参考:反向字典树
其他相似题型
745. 前缀和后缀搜索
2416. 字符串的前缀分数和
212.单词搜索 II
472.连接词
1032.字符流