归并排序(非递归实现) 计数排序
上一期我们说了归并排序的递归是如何实现的,但是递归如果层次太多的话容易栈溢出,所以我们还需要掌握非递归的实现,但是我们非递归需要如何实现?
下面我们就来看一下非递归的实现
归并排序的非递归实现他并不需要栈队列这些东西来辅助实现非递归 ,可以直接改为循环
,可以直接改为循环
这里我就直接说了,如果我们想改循环的话,我们可以想一下如何改成循环,我们想一下递归
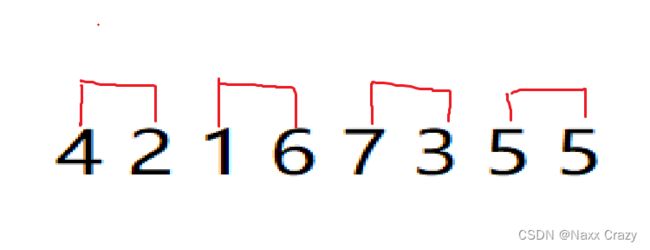
递归的时候是先分为一个一个的数值,然后两个值进行比较,然后归并,然后就依次归并,那么我们想要循环,我们可不可以直接先让两个两个数字进行比较,所以我们这里可以直接让两个两个数字比较
就像这样
我们可以直接让两个两个数字进行比较,所以等一趟循环比较结束后
这一趟结束后,就两个两个已经归并结束,所以这时候我们就四个四个一起归并
就像这样,我们把2 4和1 6认为是两组数据,然后就让他们进行归并,同时后面的两组数据也是相同的
最后就是这样
然后我们就让每四个为一组数据
就是这样,然后继续让他们进行归并
最后就归并结束
好了这个就是思想,那么我们应该如何实现呢?
我们先浅浅的看一下代码
我们还是需要一个临时数组的,用来存放归并时的临时数据,所以这时候我们就可以,定义一个gap,让gap从1开始变化,每一次都增加2,这样我们就可以实现,刚开始是一个一个排序,然后就是每两个两个排序,然后就是四个四个,知道gap大于n(整个数组的数据个数)就结束了
所以我们就可以实现归并
所以下面的代码就是这样
下面就是定义一个j初始为i,然后进行比较然后拷贝,这样就可以 ,等每一次归并结束后,把tmp里面的数据拷贝回原数组就可以了
但是真的是这样就结束了吗?
其实并不是,我们可以想一下,如果我们里面的数据并不是2的指数倍的时候是什么样子的,我们可以仔细想一下,我们此时的gap每一次都以2倍增加,所以我们肯定会有越界,所以我们这时候就需要对我们定义的begin1和end1以及begin2和end2进行调整
我们可以想一下
但是我们这四个变量都需要调整吗?
这里我们看到我们这四个变量,那么我们四个变量都会越界吗?如果有哪些越界了我们需要调整呢?哪些越界之后我们还需要归并吗?哪些越界之后我们就不需要归并了,我们想一下
我们的begin1会不会越界?
显然不会的,因为我们的begin1每一次都是i而我们的i又是小于n的所以我们的begin1不会越界,但是我们的end1会越界吗?会的
所以,既然我们的end1都会越界,所以后面的两个也当然是会越界的,而我们这三个变量越界后的处理也当然是不一样的
如果我们的end1越界了,那么我们还需要对该数组进行归并吗?
我们想一下,如果我们的end1越界,说明我们只有一组甚至是一组都不到的数据,所以我们只有一组数据当然是不用归并的,那么我们的begin2越界呢?
如果我们的begin2越界,也说明我们只有一组数据,也是不用归并的,所以我们这里就可以直接不归并,那么我们的end2越界呢?
我们的end2越界,说明我们现在至少有一组多的数据,所以我们这里是需要归并的,那么我们应该怎么样调整呢?
我们可以看一下
和我们上面所说的一样,我们如果是end1或者begin2越界的话,说明我们只有一组数据,并不需要归并,如果我们的end2越界,说明我们有一组多的数据,是需要归并的,所以我们只需要把end2调整为不会越界就可以了
下面我们看一下整体的代码
其实上面只是一种写发,这种写法是每归并一次就拷贝一次,还有一种是一组全部归并好后,才进行拷贝,其实两种写法都是差不多的,这里把下面的一种也贴出来
OK 这就是归并排序的非递归,下面讲一下计数排序
我们前面说的几种排序都是比较排序,而计数排序是非比较排序
下面我们就来看一下计数排序,这里就直接说计数排序的思想以及用途了
这里的计数排序是特殊情况下使用的,可是他适用于什么情况呢?他适用于数字比较集中的排序,如果是这种情况他的时间复杂度特别好,已经能达到O(N),所以他在特定时候是特别厉害的
这里就说一下如何实现
计数排序他可以开一段数组,这段数组用来映射,就像这样
如果我们是这一组数据的话,那么我们如何排序呢?
这里直接说思想,我们先开一段数组,然后把他里面初始化为0,然后这里把上面的一组数据依次遍历一遍,然后使用映射,下面看图片
这里首先是0,然后再0位置++,然后遍历到下一个数字,
然后到5的位置++,就这样依次下去
然后是这样,知道这一组数字结束
但是这样是有缺点的
我们看图片
如果是这一组数据的话,那么我们可以看到,我们这一组数据会集中于后面
我们只能使用后面的这一组空间
但是我们前面的这么多空间都会浪费掉,所以我们需要想一个解决办法
绝对映射会浪费太多的空间,那么我们就可以使用相对映射
我们可以这样
我们就可以找到里面的最大值,和最小值,然后算出他们的差,然后我们就只需要开差距大小的空间就可以了,我们在计数排序的时候只需要让每个数字-掉最小值就可以了,就像这样
就是这样,所以我们现在可以直接看代码了
我们看明白思想之后看代码应该就是很容易了,所以这里也就不多解释
今天结束