主成分分析法（PCA方法）的理论与代码实现
序
这个，怎么实现？
不知道，这是个数学问题，还是个编程问题。
找了个网页：
http://blog.codinglabs.org/articles/pca-tutorial.html
http://blog.codinglabs.org/articles/pca-tutorial.html网页不咋生动，又找了个视频：
https://www.bilibili.com/video/BV1E5411E71z?spm_id_from=333.337.top_right_bar_window_custom_collection.content.clickhttps://www.bilibili.com/video/BV1E5411E71z?spm_id_from=333.337.top_right_bar_window_custom_collection.content.click
作为一个小小白，脑子也不好使。对于学习这件事，也不指望学会，不指望全如意；你自己尽力，有个半称心就行了。
实在学不会，被别人拿去笑话一下，给别人长一点自信，当个搞笑角色，也不错嘛——有输入，总会有点输出的嘛。
下面是视频里的截图。
理论介绍
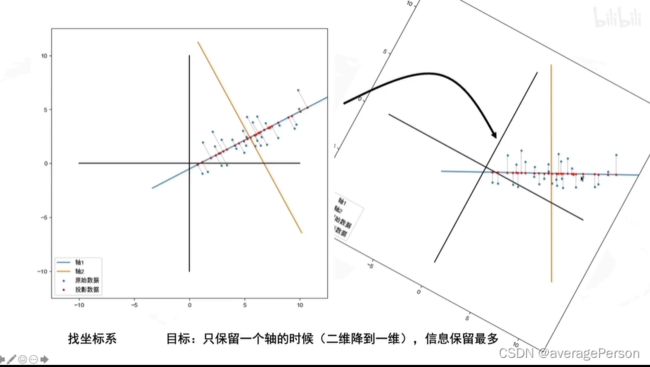
PCA的目的
PCA的过程全览
一些 预备内容
矩阵变换的介绍
拉伸
旋转
PCA的过程，其实是可逆的，互逆的。
拉伸：决定了方差最大的方向是横还是纵
旋转：决定了方差最大的方向的角度
关键是求R，R是什么？
协方差矩阵的公式：（因为去中心化了，所以平均值都是0，公式里就没这一项了）
根据上面那个公式，推到D'的协方差矩阵：
S是个对角阵，转不转置，结果一样
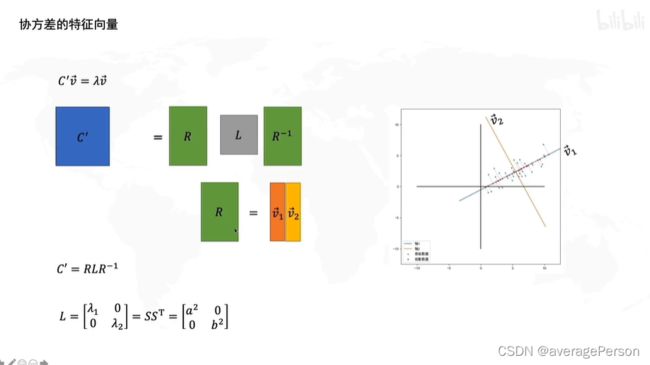
D‘的协方差矩阵，的特征向量
根据矩阵的特征向量的定义可得：
按矩阵乘法的规则组合一下
两个一列的向量可以用一个两列的向量来代替的。
拿东西，分为开门，拿，关门；三个步骤。一个行为有开门，拿，关门，三个步骤，所以这个行为叫拿东西。
变个形，发现这个推导出来的R，和旋转的那个R，是一个玩意。
所以，那俩特征向量，就是两个主成分的方向，这个信息在R里。
那俩特征值，表示沿着两个主成分被拉伸的程度，这个信息在L里。
怪不得要找最大的特征值。
L是是在R'这组基下的协方差矩阵吧？？
大概就这样吧……
借助numpy的编程实现
那末，怎么编程求这个所谓的协方差矩阵的两个特征值和特征向量啊？
找了个参考的链接，里面有代码的。
https://gitee.com/ni1o1/pygeo-tutorial/blob/master/12-.ipynbhttps://gitee.com/ni1o1/pygeo-tutorial/blob/master/12-.ipynb
实现的话，缺少一些numpy方面的知识。那就去调查研究一下嘛：
作为一个小小白，从几个简单例子开始吧
第一段
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
print(data)输出结果
参考链接
numpy的seedhttps://blog.csdn.net/qq_34840129/article/details/86096803?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873185016780261914117%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164873185016780261914117&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-2-86096803.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=numpy.random.seed&spm=1018.2226.3001.4187【Numpy】中np.random.uniform()函数用法https://blog.csdn.net/lemonxiaoxiao/article/details/109244755?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873203116780264067624%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164873203116780264067624&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-1-109244755.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=np.random.uniform&spm=1018.2226.3001.4187
第二段
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
print(data)
参考链接
Numpy.array中[:]和[::]的区别https://blog.csdn.net/zhuqiang9607/article/details/83903487?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873302316780357253756%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164873302316780357253756&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-83903487.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=numpy+%3A&spm=1018.2226.3001.4187numpy 数组X[:,0]和X[:,1]的详解https://blog.csdn.net/doubledog1112/article/details/85095571?ops_request_misc=&request_id=&biz_id=&utm_medium=distribute.pc_search_result.none-task-blog-2~all_pay~es_rank~default-2-85095571.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=numpy+%5B%3A%5D&spm=1018.2226.3001.4187python中数组切片含义解析https://blog.csdn.net/weixin_44676142/article/details/109457879?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2~default~CTRLIST~Rate-1.pc_relevant_aa&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2~default~CTRLIST~Rate-1.pc_relevant_aa&utm_relevant_index=1
第三段
# 计算以下数据的协方差矩阵
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
print(data_norm)
numpy中的mean()函数https://blog.csdn.net/lilong117194/article/details/78397329?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873387416782094885028%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164873387416782094885028&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-78397329.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=numpy+mean&spm=1018.2226.3001.4187
第四段
# 计算以下数据的协方差矩阵
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
#print(data_norm)
X = data_norm[:,0]
Y = data_norm[:,1]
# 定义一个函数，输入X，Y能得到X，Y之间的协方差
def getcov(X,Y):
covxy = ((X-X.mean())*(Y-Y.mean())).sum()/(len(X)-1)
return covxy
print (getcov(X,X))#这里求的是X的方差
print(getcov(Y,Y))#Y的方差
print(getcov(X,Y))#协方差
第五段
# 计算以下数据的协方差矩阵
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
#print(data_norm)
X = data_norm[:,0]
Y = data_norm[:,1]
# 定义一个函数，输入X，Y能得到X，Y之间的协方差
def getcov(X,Y):
covxy = ((X-X.mean())*(Y-Y.mean())).sum()/(len(X)-1)
return covxy
print (getcov(X,X))#这里求的是X的方差
print(getcov(Y,Y))#Y的方差
print(getcov(X,Y))#协方差
#numpy自带了协方差矩阵的计算方法，验证一下
C = np.cov(data_norm.T)#为什么要转置？
print(C)
为什么要转置一下？
官方文档里这么说的
这还有个中文翻译版的官方文档：
Numpy入门(十)：np.cov()用法https://blog.csdn.net/weixin_46348799/article/details/108963194?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873551916780274141001%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164873551916780274141001&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-1-108963194.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=np.cov&spm=1018.2226.3001.4187
第六段
受上面那个中文翻译版的官方文档的启发，摸索了一下：
结果一样的。
# 计算以下数据的协方差矩阵
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
#print(data_norm)
X = data_norm[:,0]
Y = data_norm[:,1]
# 定义一个函数，输入X，Y能得到X，Y之间的协方差
def getcov(X,Y):
covxy = ((X-X.mean())*(Y-Y.mean())).sum()/(len(X)-1)
return covxy
print (getcov(X,X))#这里求的是X的方差
print(getcov(Y,Y))#Y的方差
print(getcov(X,Y))#协方差
#numpy自带了协方差矩阵的计算方法，验证一下
C = np.cov(data_norm.T)#为什么要转置？因为一个参数表示一个变量，所以要把10*2转置成2*10
print(C)
C=np.cov(data_norm,rowvar=False)## 此时列为变量计算方式 即X为列，Y也为列
print(C)
第七段
然后，这个协方差矩阵的特征值和特征向量，怎么算？口算？
# 计算以下数据的协方差矩阵
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
X = data_norm[:,0]
Y = data_norm[:,1]
C=np.cov(data_norm,rowvar=False)## 此时列为变量计算方式 即X为列，Y也为列
#计算特征值和特征向量
vals, vecs = np.linalg.eig(C)
#重新排序，从大到小
vecs = vecs[:,np.argsort(-vals)]
vals = vals[np.argsort(-vals)]
print(vecs)
print(vals)
如何计算方阵的特征值和特征向量np.linalg.eig()https://blog.csdn.net/qq_38048756/article/details/112543075?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873654816781685326133%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164873654816781685326133&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-3-112543075.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=np.linalg.eig&spm=1018.2226.3001.4187
Numpy学习之np.argsort()函数https://blog.csdn.net/m0_46457700/article/details/109408524?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1.pc_relevant_default&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1.pc_relevant_default&utm_relevant_index=2【Python语法】X[:,0]和X[:,1] 什么意思？https://blog.csdn.net/Higan_MM/article/details/90410095?ops_request_misc=&request_id=&biz_id=102&utm_term=%E3%80%90%EF%BC%9A%EF%BC%8C0%E3%80%91&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-90410095.nonecase&spm=1018.2226.3001.4187
这是一个手算特征值和计算机算的对比的例子，挺形象的。可以直观的看出，特征向量是按列看的。不是按行看的。
python — numpy计算矩阵特征值，特征向量https://blog.csdn.net/pentiumCM/article/details/105652853?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2~default~CTRLIST~TopBlog-1.topblog&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2~default~CTRLIST~TopBlog-1.topblog&utm_relevant_index=1
第八段（小结）
# 计算以下数据的协方差矩阵
import numpy as np
np.random.seed(0)#随机数种子
data = np.random.uniform(1,10,(10,2))
data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
X = data_norm[:,0]
Y = data_norm[:,1]
C=np.cov(data_norm,rowvar=False)## 此时列为变量计算方式 即X为列，Y也为列
#计算特征值和特征向量
#这个返回的特征向量，要按列来看
vals, vecs = np.linalg.eig(C)
#重新排序，从大到小
#默认从小到大排列,这里取负了，就是从大到小排列，返回相应索引
vecs = vecs[:,np.argsort(-vals)]#特征向量按列取，这里就呼应上了
vals = vals[np.argsort(-vals)]
print(vals)
print(vecs)
#第一个特征值对应的特征向量
print(vals[0],vecs[:,0])
#第二个特征值对应的特征向量
print(vals[1],vecs[:,1])这个特征向量都是长度单位化以后的。
NumPy.array 求点乘， 向量长度， 向量夹角的方法https://blog.csdn.net/qq_32424059/article/details/100874358?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164873936216781685383416%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=164873936216781685383416&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-1-100874358.142%5Ev5%5Epc_search_insert_es_download,143%5Ev6%5Eregister&utm_term=numpy+%E5%90%91%E9%87%8F%E9%95%BF&spm=1018.2226.3001.4187
实际应用
怎么实际运用呢？更是一个大问题。这个矛盾解决了那个矛盾又出来了，矛盾也有新陈代谢。没有矛盾就没有世界呐。
第一段
简单测试了一下：
# 计算以下数据的协方差矩阵
import numpy as np
# np.random.seed(0)#随机数种子
# data = np.random.uniform(1,10,(10,2))
# data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#不用随机数了，这次用一个比较实际的例子，来测试PCA准不准
#假设这是一个扁扁的矩形
input=list()
input.append([100,100])
input.append([500,100])
input.append([100,200])
input.append([500,200])
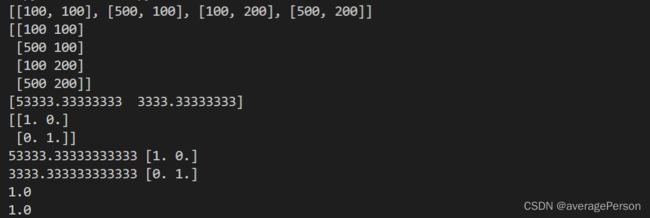
print(input)
#从已有的数组创建数组
data=np.asarray(input)
print(data)
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
X = data_norm[:,0]
Y = data_norm[:,1]
C=np.cov(data_norm,rowvar=False)## 此时列为变量计算方式 即X为列，Y也为列
#计算特征值和特征向量
#这个返回的特征向量，要按列来看
vals, vecs = np.linalg.eig(C)
#重新排序，从大到小
#默认从小到大排列,这里取负了，就是从大到小排列，返回相应索引
vecs = vecs[:,np.argsort(-vals)]#特征向量按列取，这里就呼应上了
vals = vals[np.argsort(-vals)]
print(vals)
print(vecs)
#第一个特征值对应的特征向量
print(vals[0],vecs[:,0])
#第二个特征值对应的特征向量
print(vals[1],vecs[:,1])
#计算模长是否为1
print(np.linalg.norm(vecs[:,0]))
print(np.linalg.norm(vecs[:,1]))
NumPy 从已有的数组创建数组https://www.runoob.com/numpy/numpy-array-from-existing-data.html
第二段
这一大堆数字，不直观呐。能把结果可视化一下吗？
# 计算以下数据的协方差矩阵
import numpy as np
import matplotlib.pyplot as plt
# np.random.seed(0)#随机数种子
# data = np.random.uniform(1,10,(10,2))
# data[:,1:] = 0.5*data[:,0:1]+np.random.uniform(-2,2,(10,1))
#不用随机数了，这次用一个比较实际的例子，来测试PCA准不准
#假设这是一个扁扁的矩形
input=list()
input.append([100,100])
input.append([500,100])
input.append([100,200])
input.append([500,200])
print(input)
#从已有的数组创建数组
data=np.asarray(input)
print(data)
#去中心化
data_norm = data-data.mean(axis = 0)#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
X = data_norm[:,0]
Y = data_norm[:,1]
C=np.cov(data_norm,rowvar=False)## 此时列为变量计算方式 即X为列，Y也为列
#计算特征值和特征向量
#这个返回的特征向量，要按列来看
vals, vecs = np.linalg.eig(C)
#重新排序，从大到小
#默认从小到大排列,这里取负了，就是从大到小排列，返回相应索引
vecs = vecs[:,np.argsort(-vals)]#特征向量按列取，这里就呼应上了
vals = vals[np.argsort(-vals)]
print(vals)
print(vecs)
#第一个特征值对应的特征向量
print(vals[0],vecs[:,0])
#第二个特征值对应的特征向量
print(vals[1],vecs[:,1])
#计算模长是否为1
print(np.linalg.norm(vecs[:,0]))
print(np.linalg.norm(vecs[:,1]))
#用画图的方式，画出结果
#设置图大小
size = 600
plt.figure(1,(8,8))
plt.scatter(data[:,0],data[:,1],label='origin data')
i=0
ev = np.array([vecs[:,i]*-1,vecs[:,i]])*size
ev = (ev+data.mean(0))
plt.plot(ev[:,0],ev[:,1],label = 'eigen vector '+str(i+1))
i=1
ev = np.array([vecs[:,i]*-1,vecs[:,i]])*size
ev = (ev+data.mean(0))
plt.plot(ev[:,0],ev[:,1],label = 'eigen vector '+str(i+1))
#plt.plot(vecs[:,1]*-10,vecs[:,1]*10)
#画一下x轴y轴
plt.plot([-size,size],[0,0],c='black')
plt.plot([0,0],[-size,size],c='black')
plt.xlim(-size,size)
plt.ylim(-size,size)
plt.legend()
plt.show() 
相关链接
Matplotlib 教程https://www.runoob.com/matplotlib/matplotlib-tutorial.html中间还遇到了点问题：
就是这段没理解好：
print(vecs)
print(vecs[:,0]*-100)
print(vecs[:,0]*100)
plt.plot(vecs[:,0]*-100,vecs[:,0]*100)
脑子里觉得应该是（-100，0）到（100，0）水平的，结果画出来是这样的：
——plot到底是横着看的还是竖着看的？
又仔细看了下以后，发现都是竖着看的，前面看错了
要是能用动画做出来就好了，图形不断变，主成分轴不断求，不过那玩意不是刚需。暂时忽略。
后记
简单测试，，意思就是复杂点的情况还不知道怎么处理。
多少也算有一点东西出来了，虽然不是什么大的东西。作为一个小小白，已经很不错了。