优先级队列(堆)【Java数据结构】
目录
1. 优先级队列
1.1概念
2. 优先级队列的模拟实现
2.1 堆的概念
2.2堆的存储方式
2.3 堆的创建
2.3.1 堆的向下调整
2.3.2 堆的创建(创建大根堆)
2.4 堆的插入与删除
2.4.1 堆的插入
2.4.2堆的删除
3.常用接口介绍
3.1 PriorityQueue的特性
3.2 PriorityQueue常用接口介绍
4. top-k问题
1. 优先级队列
1.1概念
前面介绍过队列,队列是一种先进先出 (FIFO) 的数据结构 ,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话。
在这种情况下,我们的数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象 。 这种数据结构就是优先级队列 (Priority Queue)。
2. 优先级队列的模拟实现
JDK1.8中的 PriorityQueue 底层使用了堆的数据结构,而堆实际就是在完全二叉树的基础之上进行了一些元素的调整。
2.1 堆的概念
如果有一个集合 K = {k0 , k1 , k2 , … , kn-1} ,把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0 , 1 , 2… ,则 称为 小堆 (或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;堆总是一棵完全二叉树。
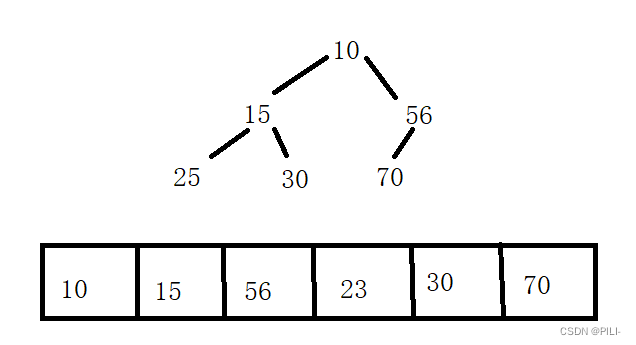
小根堆:
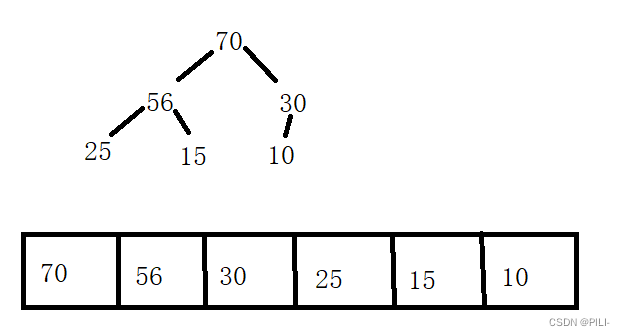
大根堆:
2.2堆的存储方式
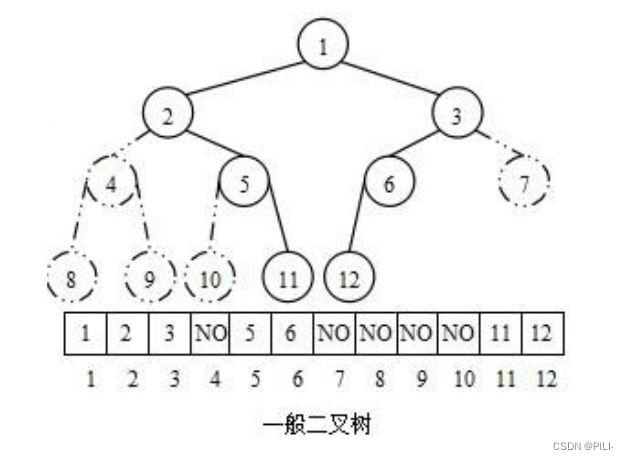
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。注意: 对于非完全二叉树,则不适合使用顺序方式进行存储 ,因为为了能够还原二叉树, 空间中必须要存储空节 点,就会导致空间利用率比较低。如下图:
将元素存储到数组中后,可以根据二叉树的性质对树进行还原,假设i为节点在数组中的下标,则有:
如果 i 为 0 ,则 i 表示的节点为根节点,否则 i 节点的双亲节点为 (i - 1)/2如果 2 * i + 1 小于节点个数,则节点 i 的左孩子下标为 2 * i + 1 ,否则没有左孩子如果 2 * i + 2 小于节点个数,则节点 i 的右孩子下标为 2 * i + 2 ,否则没有右孩子
2.3 堆的创建
2.3.1 堆的向下调整
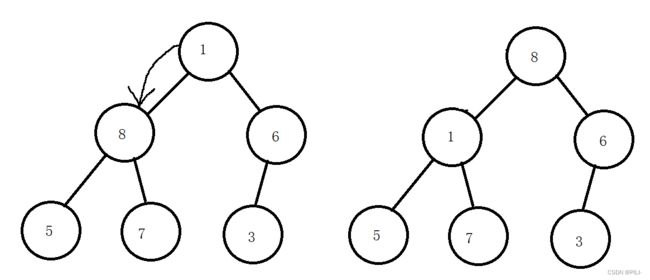
1. 让parent标记需要调整的节点,child标记parent的左孩子;因为parent如果有孩子一定先是有左孩子,再有右孩子。
2. 如果parent的左孩子存在,即:child < size(size为节点个数), 进行以下操作,直到parent的左孩子不存在。
a.判断parent是否有右孩子,如果存在,就比较左右孩子,找到左右孩子中最小的,用child进行标记。
b.将parent与child的标记值进行比较,如果parent小于child,调整结束;如果parent大于child,交换parent与child。在交换完成后,parent作为新的根结点的左子树和右子树也有可能不满足小根堆的性质,因此要继续往下调整,parent = child,child = 2*child+1,然后继续步骤2。
整体如下图所示:
public void shiftDown(int[] array, int parent) {
// child先标记parent的左孩子,因为parent可能右左没有右
int child = 2 * parent + 1;
int size = array.length;
while (child < size) {
// 如果右孩子存在,找到左右孩子中较小的孩子,用child进行标记
if(child+1 < size && array[child+1] < array[child]){
child += 1;
}
// 如果双亲比其最小的孩子还小,说明该结构已经满足堆的特性了
if (array[parent] <= array[child]) {
break;
}else{
// 将双亲与较小的孩子交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
parent = child;
child = parent * 2 + 1;
}
}
}注意:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
时间复杂度:最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为 O(log2 (n))(表示以2为底)
2.3.2 堆的创建(创建大根堆)
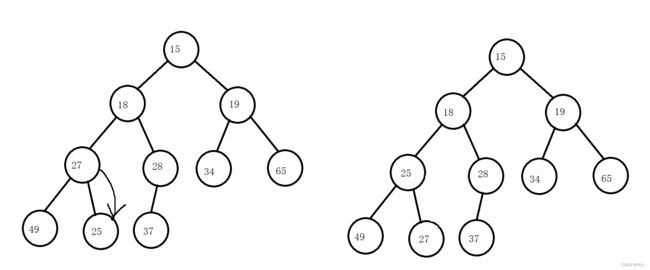
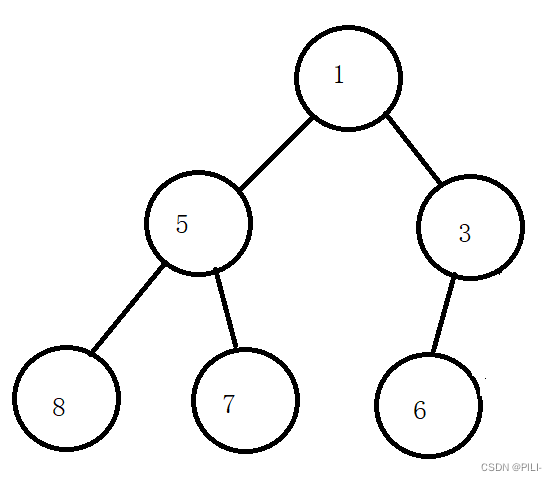
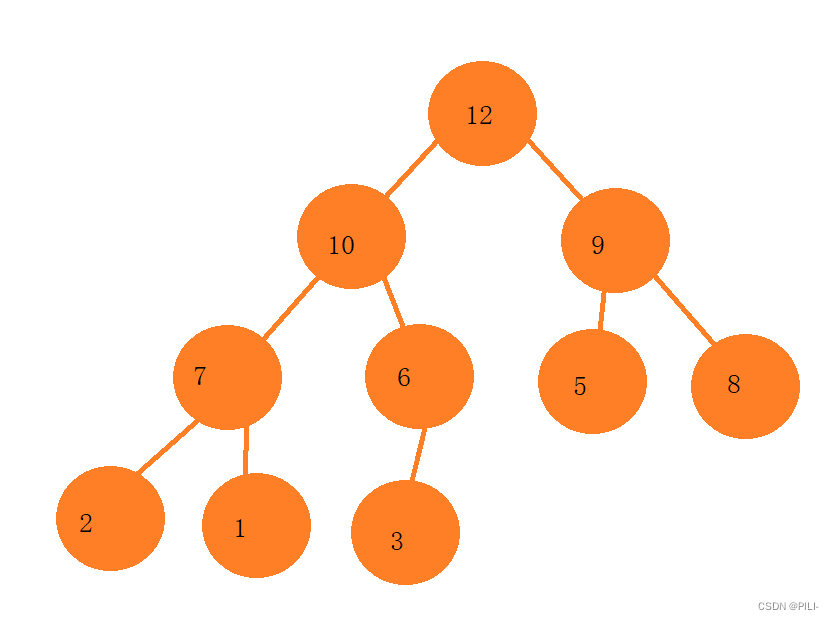
要从最后一个节点的双亲节点开始,依次向下调整。每一个节点都需要保证其左右子树可以形成大根堆!步骤:先找到倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,每遇到一个节点,都应该进行向下调整。
第一步:
第二步:
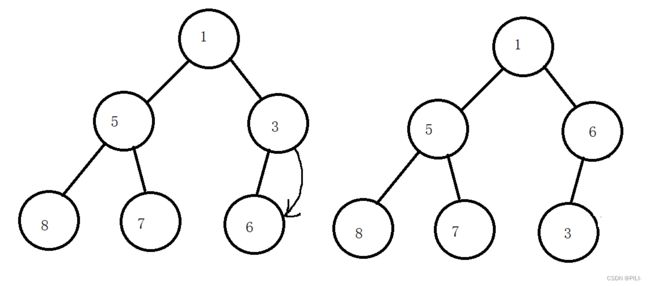
第三步:这一步需要注意,在调换8和1的位置后,原本由8为根节点构成的树就不再构成最大根堆了,因此需要对其进行重新构造堆。
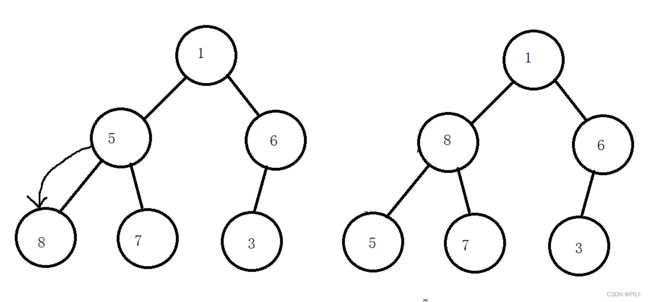
第四步:
i节点的双亲节点为 (i - 1)/2 。
public static void createHeap(int[] array) {
int root = ((array.length-1-1)>>1); //array.length-1为最后一个叶子节点
for (; root >= 0; root--) {
shiftDown(array, root);
}
}此方式建堆的时间复杂度为O(N)。
2.4 堆的插入与删除
2.4.1 堆的插入
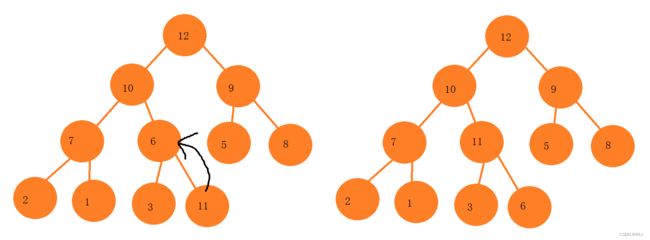
堆的插入总共需要两个步骤:1. 先将元素放入到底层空间中。2. 将最后新插入的节点向上调整,直到满足堆的性质。
先将元素插入到堆的末尾,即最后一个孩子后。
插入之后如果堆的性质被破坏,将新插入节点顺着双亲往上调整至合适位置即可。
向上调整: (大根堆)
思路和向下调整类似:先找到child的节点,如果双亲比孩子大,parent满足大根堆的性质,调整结束。如果不满足性质就交换值,继续向上调整,直到满足大根堆的性质了或者child已经是根节点。
插入11
public void shiftUp(int[] array,int child) {
// 找到child的双亲
int parent = (child - 1) / 2;
while (child > 0) {
// 如果双亲比孩子大,parent满足堆的性质,调整结束
if (array[parent] > array[child]) {
break;
}else{
// 将双亲与孩子节点进行交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
// 小的元素向下移动,可能到值子树不满足对的性质,因此需要继续向上调增
child = parent;
parent = (child - 1) / 1;
}
}
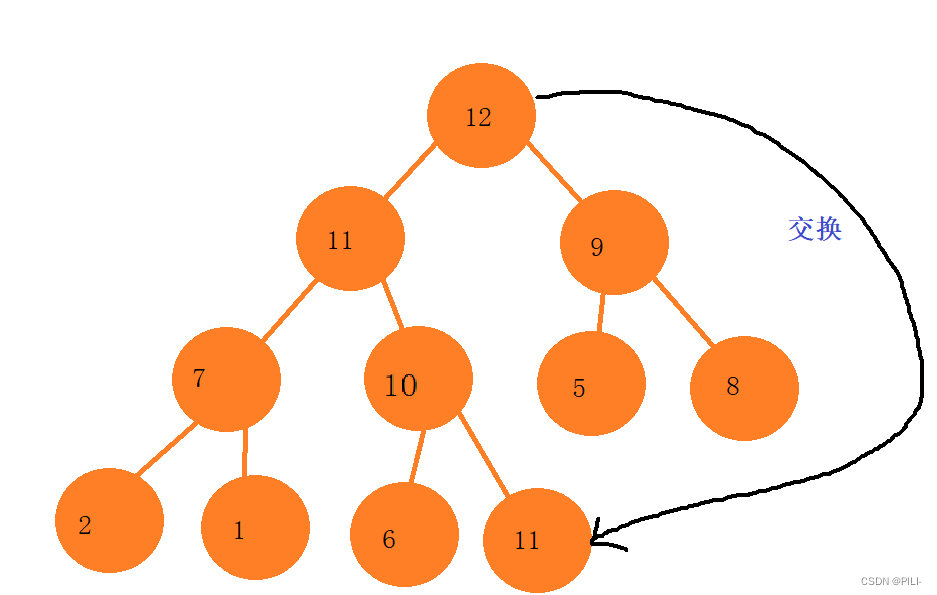
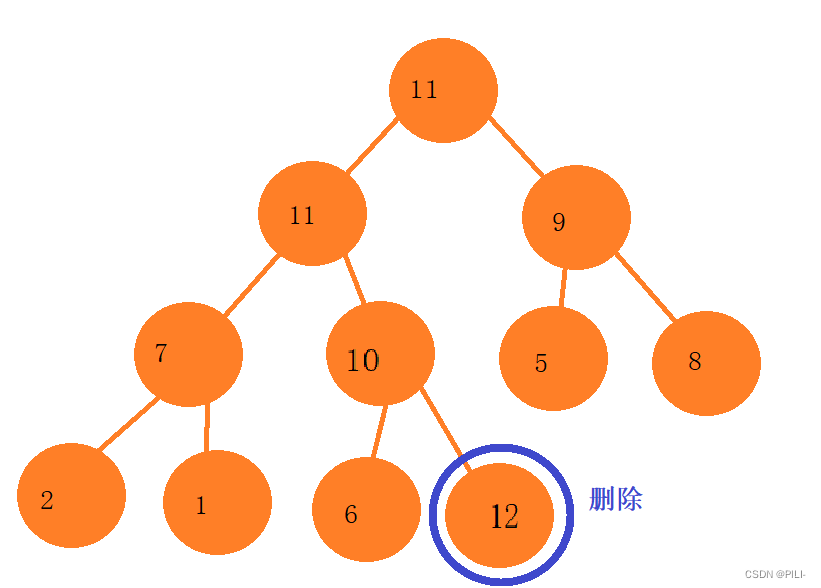
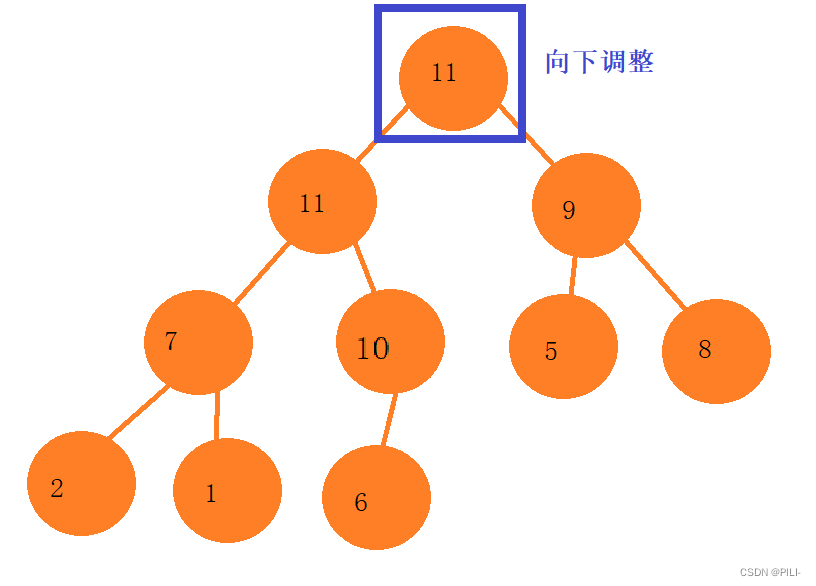
}2.4.2堆的删除
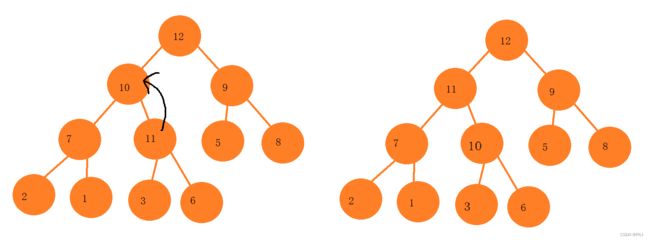
注意:堆的删除一定删除的是堆顶元素。
步骤:1. 将堆顶元素对堆中最后一个元素交换。2. 将堆中有效数据个数减少一个。3. 对堆顶元素进行向下调整。
3.常用接口介绍
3.1 PriorityQueue的特性
Java集合框架中提供了 PriorityQueue 和 PriorityBlockingQueue 两种类型的优先级队列, PriorityQueue是线 程不安全的,PriorityBlockingQueue是线程安全的 ,本文主要介绍 PriorityQueue。
关于PriorityQueue的使用要注意:
1. 使用时必须导入PriorityQueue所在的包,即:import java.util.PriorityQueue;
2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常。3. 不能插入null对象,否则会抛出NullPointerException。4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容。5. 插入和删除元素的时间复杂度为O(log2(N)) (以2为底)6. PriorityQueue底层使用了堆数据结构。7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素。
3.2 PriorityQueue常用接口介绍
1. 优先级队列的构造
|
构造器
|
功能介绍
|
|---|---|
|
PriorityQueue()
|
创建一个空的优先级队列,默认容量是 11
|
|
PriorityQueue(int
initialCapacity)
|
创建一个初始容量为 initialCapacity 的优先级队列,注意:
initialCapacity 不能小于 1 ,否则会抛 IllegalArgumentException 异
常
|
|
PriorityQueue(Collection
extends E> c)
|
用一个集合来创建优先级队列
|
注意:默认情况下,PriorityQueue队列是小堆,如果需要大堆需要用户提供比较器。
用户自己定义的比较器:直接实现Comparator接口,然后重写该接口中的compare方法即可
//自己定义比较器,来实现大根堆
class intCmp implements Comparator {
@Override
public int compare(Integer o1, Integer o2) {
//return o1.compareTo(o2); // 小根堆
return o2.compareTo(o1); // 大根堆
}
}
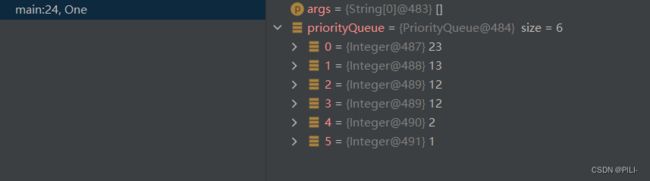
public class Test{
public static void main(String[] args) {
PriorityQueue priorityQueue = new PriorityQueue<>(new intCmp());
priorityQueue.offer(12);
priorityQueue.offer(12);
priorityQueue.offer(23);
priorityQueue.offer(13);
priorityQueue.offer(2);
priorityQueue.offer(1);
System.out.println("asd");
}
} 可以看出在自己定义了比较器之后,就变为了大根堆了。
这里应掌握另一种写法:匿名内部类写法
public static void main(String[] args) {
//匿名内部类
PriorityQueue priorityQueue = new PriorityQueue<>(new Comparator() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
} 2. 插入/删除/获取优先级最高的元素
|
函数名
|
功能介绍
|
|---|---|
|
boolean
offffer(E e)
|
插入元素 e ,插入成功返回 true ,如果 e 对象为空,抛出 NullPointerException 异常,时
间复杂度O(log2(N)) (以2为底)
,注意:空间不够时候会进行扩容
|
|
E peek()
|
获取优先级最高的元素,如果优先级队列为空,返回 null
|
|
E poll()
|
移除优先级最高的元素并返回,如果优先级队列为空,返回 null
|
|
int size()
|
获取有效元素的个数
|
|
void
clear()
|
清空
|
|
boolean
isEmpty()
|
检测优先级队列是否为空,空返回 true
|
注意:以下是JDK 1.8中,PriorityQueue的扩容方式(理解即可):
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
if (minCapacity < 0) // overflow
throw new OutOfMemoryError();
return (minCapacity > MAX_ARRAY_SIZE) ?
Integer.MAX_VALUE :
MAX_ARRAY_SIZE;
}优先级队列的扩容说明:
如果容量小于 64 时,是按照 oldCapacity 的 2 倍方式扩容的如果容量大于等于 64 ,是按照 oldCapacity 的 1.5 倍方式扩容的如果容量超过 MAX_ARRAY_SIZE ,按照 MAX_ARRAY_SIZE 来进行扩容
4. top-k问题
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
思路:首先要找最小的k个数,我们需要创建一个大根堆,这个大根堆里面含有k个节点,也就是数组前k个元素形成大根堆,从第k+1个元素开始,每一个元素都与大根堆的根节点进行比较,若大于根节点,可直接略过,若小于根节点,根节点出堆,该元素进入大根堆,此时大根堆内的k个元素就是目前已经遍历的元素里最小的k个元素,一直到结束,就可找出最小的k个数。
public int[] smallestK(int[] arr, int k) {
if( k < 1){
return new int[0];
}
//1. 建立一个大根堆
PriorityQueue temp = new PriorityQueue<>(k,new Comparator(){
public int compare(Integer a,Integer b){
return b.compareTo(a);
}
});
for(int i=0;i