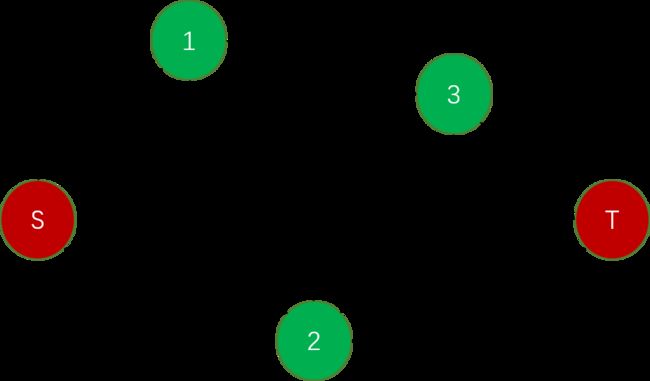
(图论)最大流算法-7.29讲解

最大流算法

网络流基础概念

网络流

在一个有向图G=(V,E)G=(V,E)中：

有一个唯一的源点S(入度为00：出发点)
有一个唯一的汇点T(出度为00：结束点)
图中的每一条边都一个非负的权值，这个权值叫做容量c(u,v)c(u,v)
满足上述条件的图GG称为网络流图，记为G=(V,E,C)G=(V,E,C)

可以想象成，如果把每条边都看成一个管道，可以看成是水从源点S出发经过这些管道，最终流向汇点T，而每条管道有最大的容量。（地下排水管道）

可行流

流量：每条弧上给定一个实数f(u,v)f(u,v)，满足0≤f(u,v)≤c(u,v)0≤f(u,v)≤c(u,v)

可行流满足：

源点S：流出量 = 整个网络的流量
汇点T：流入量 = 整个网络的流量
中间的点：总流入量 = 总流出量，同时0≤f(u,v)≤c(u,v)0≤f(u,v)≤c(u,v)
这样的在整个网络中的流量就是可行流，可行流有多个

最大流

所有可行流中流量最大的流量

最大流可能不止一个

求解最大流

建立反向边（寻找增广路径增加最大流）：
首先要明白一点，在一条从S到T的路径中，能够带来的最大流量取决于这条路径上的最小容量。

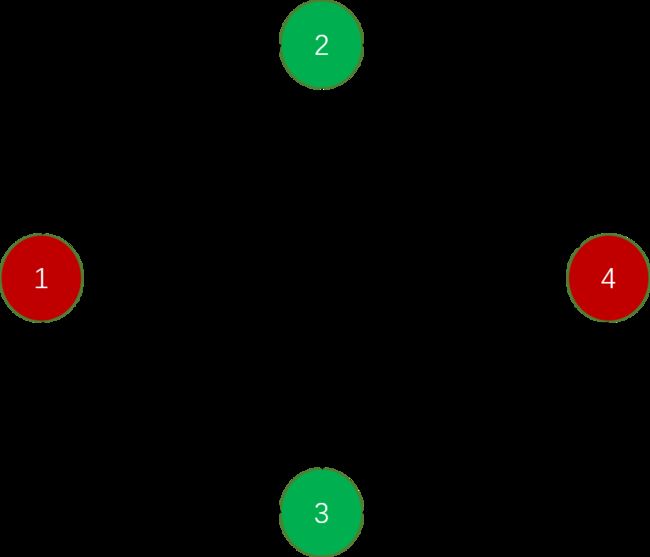
如果我们使用搜索算法找一条从1到4的路径，并且这条路径能够带来的流量是这条路径上边的容量的最小值，

假设我们找到的路径是1−>2−>3−>4，现在的流量是1，因为这条路已经使用过了，把这条路径上的每条边减1，再次找从1到4的路径，发现找不到了，因此得到的答案为1，但是正确的答案应该是2。即1−>2−>4、1−>3−>4

这个时候，为了能够继续找到路径，必须要反向建立边，把当前路径反向建边，边的权值就是这条路径的流量

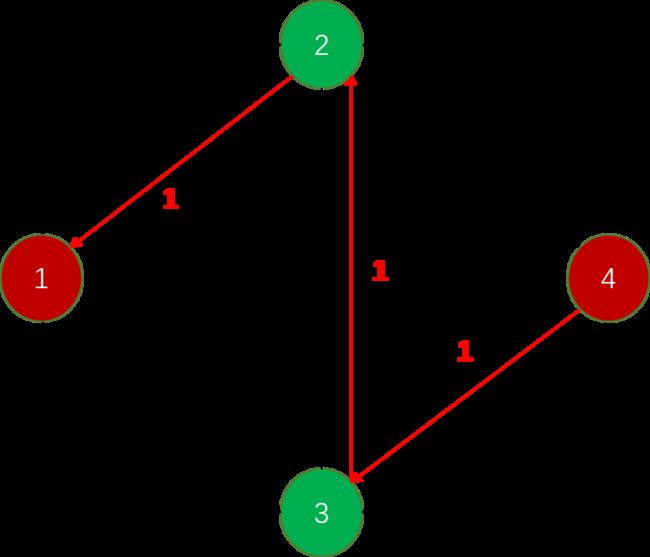
其中红色的边就是反向建立的，这个时候继续寻找一条路径，发现可以走1−>3−>2−>4，带来的流量是1，然后继续找寻路径，发现没有可达的路径了，因此最大流是1+1=2。

为什么要反向建边呢，仔细想想应该能够明白，反向建立边的作用相当于让之前的路径有可以反悔的余地。这样即使一开始走错也没有关系，因为可以通过反向边来反悔，最终一定能得到正确答案

增广路径

明白了反向建边后，来看什么是增广路经？

如果一个可行流不是最大流，那么当前网络中一定存在一条增广路经。

从源点S到汇点T的一条路径中，如果边(u,v)与该路径的方向一致就称为正向边，否则就记为逆向边，如果在这条路径上的所有边满足

正向边f(u,v) 逆向边f(u,v)>0
则该路径是增广路径

其实增广路径就是通过这样一条路径，来增加到达汇点的流量，而路径中的流量没到达容量。

(在上图中，其实每次找到的一条从1到4的路径都是一条增广路径)

沿这条增广路改进可行流的操作称为增广.所有可能的增广路径放在一起就构成了残余网络

模板题：

蓝桥杯算法训练 网络流裸题ALGO-247 2020-03-27
资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
　　一个有向图，求1到N的最大流
输入格式
　　第一行N M，表示点数与边数
　　接下来M行每行s t c表示一条从s到t的容量为c的边
输出格式
　　一个数最大流量
样例输入
6 10
1 2 4
1 3 8
2 3 4
2 4 4
2 5 1
3 4 2
3 5 2
4 6 7
5 4 6
5 6 3
样例输出
8

数据约定：
n<=1000 m<=10000

最大网络流
从找源点（即题中的1）到汇点（N）的最大流。
一个经典的例子

如果走 1 -> 2 ->3 -> 4 这条路
然后再1->2->4
那么最后的结果是1+1=2

但我们可以看出来这题最优的走法是1 - >2 -> 4 然后 1 -> 3 -> 4
最大流是2+1=3

所以要找一个可以后悔的方法，那就是对每条边加一条反向的边

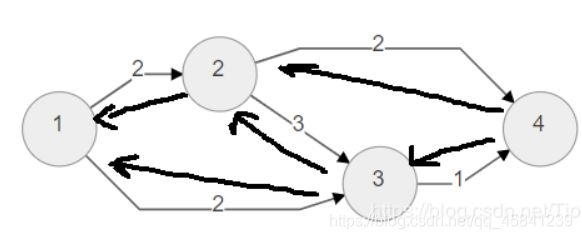
初始时 每条边的反向的边的容量都是0 当走过一条路之后，这条路正向的容量变为 正向容量 -= 流过的流量 ，而反向流量 += 流过的流量。
一条路正向走一遍，反向再走一遍时，那么这条路上正向流通的量就会被反向流通的量抵消掉一部分
拿上面的例子来说，当第一次走了 1 -> 2 ->3-> 4 时，对2-> 3 后悔的路就会被打开,而 1 -> 2 ->3-> 4 流通的量是1，所以2->3 变为 3-1=2，3->2 变为0+1=1。且1->2 变为2-1=1，3->4 变为1-1=0；(例子中没用的反向的路就不画出来了)

第一次： 1->2 ->3 ->4

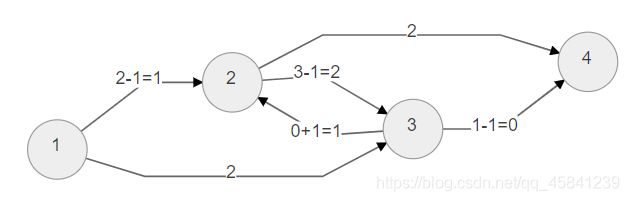
第二次： 1->2 ->4

第三次：1->3->2->4

最后：

再从源点1出发的时候 当我们走到 汇点4 流通的量是0 则已经没有可以流通的量了，结束

代码描述

首先用一个map存放边，需要注意的是题中可能重复对一条路输入，就是说输入s t c的时候可能出现1 2 1 下一次输入又出现1->2这条路 ，所以写的时候不能mp[i][j]=c，而是要mp[i][j]+=c，刚开始提交的时候一直没通过，后来发现了这个问题。
然后定义一个数组 a,a[i]代表从源点到i的最大流通量，即每次源点开始搜索，最后的a[n]就是从源点到汇点的最大流通量，我们还要定义一个数组pre，pre[i]的意义是i的前一个点。
在每一次搜索完成之后，如果a[n]==0，说明已经没有剩余可以流通的量了，直接return；否则，存放结果的res+=本次搜索的流量a[n],res+=a[n]，然后从点n开始，到1结束，更新我们这次搜索走过的路的流量，点i的上一个点就是pre[i]，所以mp[pre[i]][i]+=a[n],mp[i][pre[i]]-=a[n];

#include
#include
#include
#include
using namespace std;

int N,M;
int s,t;
int res;

map<int,map<int,int> >  mp;//描述有向图
vector<int> a;//代表当前增广路径的最大流通量
vector<int> pre;//记忆路径

void Solution(){
 	queue<int> que;
	while(1){//从源点开始找

		a.assign(N+1,0);  //初始化 a
		a[s]=INT_MAX;     //源点相当于有无限的流量
		que.push(s);      //每次都是从源点开始找
		
        while(!que.empty()){  //bfs找增广路
        	int v=que.front();
        	que.pop();
			for(map<int,int>::iterator i=mp[v].begin();i!=mp[v].end();++i){//map迭代器，以v为起点寻找所有可能的下一个点
				if(!a[i->first]&&i->second>0){
					pre[i->first]=v;//保存上一个点，后面更新路径时使用pre数组更新数据
					a[i->first]=min(a[v],i->second);//容量最小为多少，那么这条路的流量最大就是多少 
					que.push(i->first);
				}
			}
        }
        
		if(a[t]==0)return;//没有剩余的流量了
		
		res+=a[t];
		for(int i=N;i!=1;i=pre[i]){//更新走过的路的流量
			mp[pre[i]][i]-=a[t];//正向容量减去流过的流量
			mp[i][pre[i]]+=a[t];//反向容量加上流过的流量
		}
	}
}
int main(){
	cin>>N>>M;
	for(int i=0;i<M;++i){
		int k,j,l;
		cin>>k>>j>>l;
		mp[k][j]+=l;//是+= 不是= 一条边可能会重复出现
	}
	s=1;//源点
	t=N;//汇点
	pre.assign(N+1,0);
    Solution();
    cout<<res<<endl;
	return 0;
}

7.29讲解-林兆祥