Direct3D 12——图形——采样
采样会产生一些问题
产生锯齿
产生摩尔纹
人眼在时间中的采样跟不上运动的速度
这三种问题的本质就是信号的变换太快了以至于采样的速度跟不上就会产生以上这些问题
采样会导致走样本质的问题是信号的速度太快了，导致采样是速度跟不上它，这样会产生走样。
如何反走样
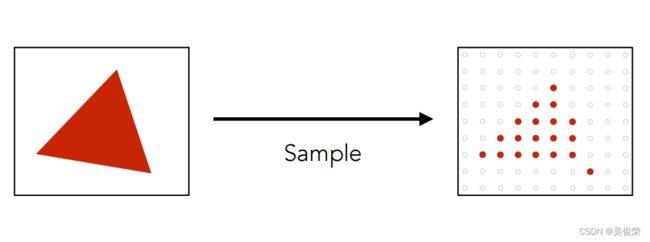
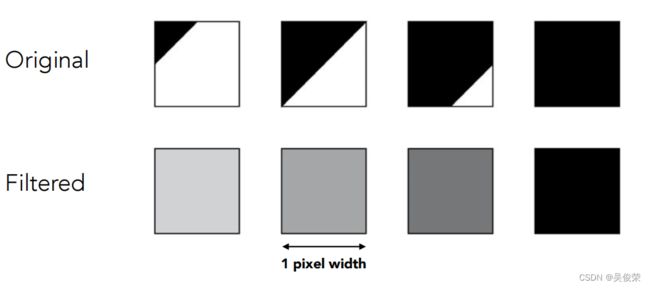
绘制三角形的时候要么是白的要么是红的 这样就会走样 。
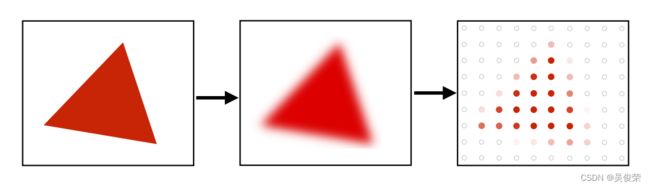
可以先把三角形做一遍模糊然后前去采样 ，可以解决走样的问题。
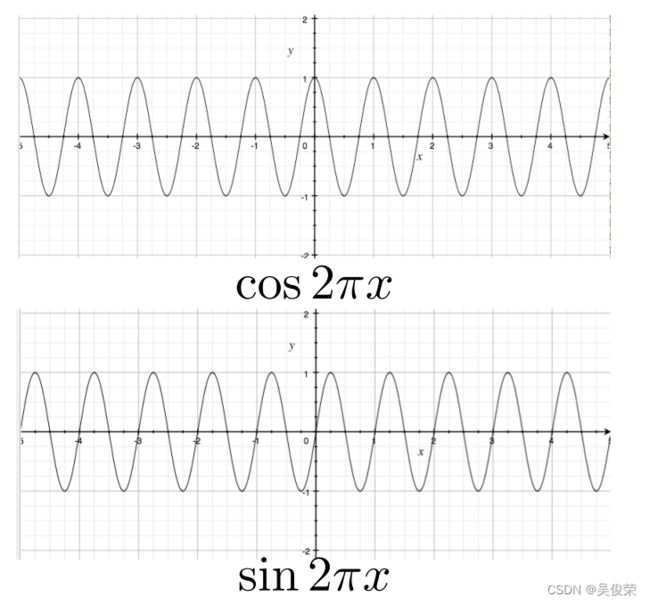
频率
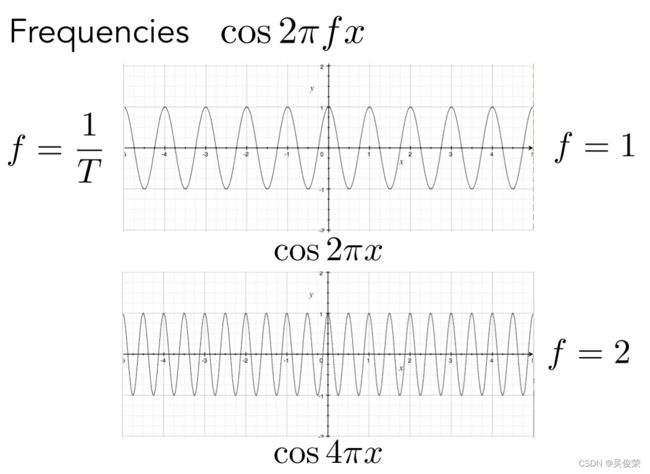
通过调整 x 前面的系数，得到不同的余弦波，他们的不同在于他们的频率不同。
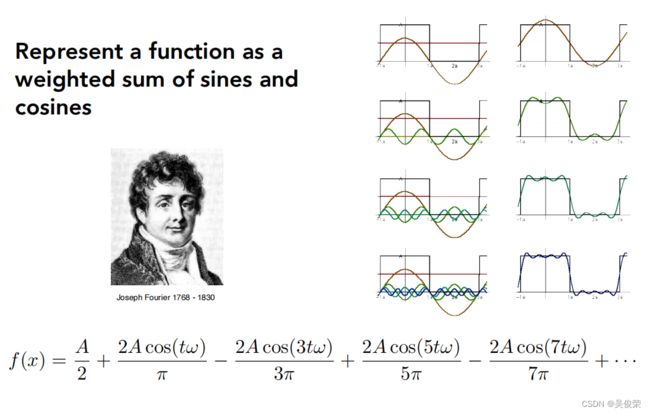
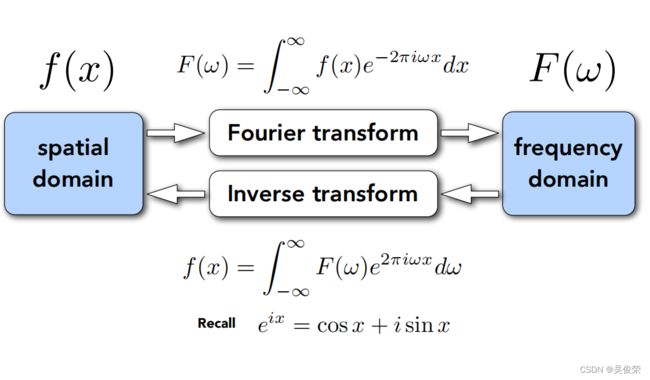
傅里叶基数展开，任何一个周期函数我都可以把它写成一系列正弦 和余弦的线性组合，以及一个常数项
傅里叶变换
傅里叶变换就是把函数变成不同频率的段
对于一个函数来说它本身就有一定的频率，采样也应该也有一定的频率。
如果函数的频率很快，采样的频率很漫，那采样的频率就跟不上函数的频率。
同样的采样方法采样不同频率的函数得出的结果我们无法区分它
滤波
滤波 就是去掉一部分频率
根据傅里叶变换绘制图片 ，低频信息集中在中间非常多，高频信息 在周围非常少
去掉低频信息，根据逆傅里叶变换回去。表示图像 的边界
去掉高频信息，根据逆傅里叶变换回去。表示相对于模糊 的
去掉高频信息和低频信息，留下某一端频率
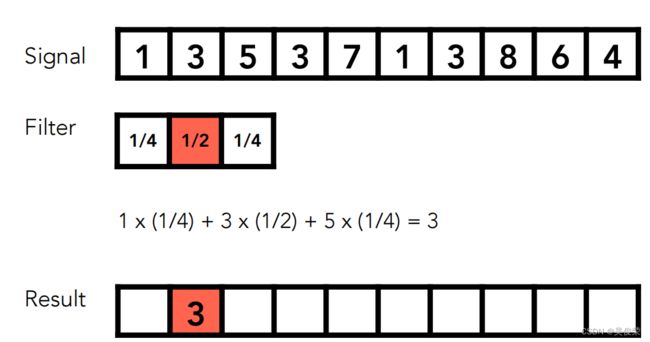
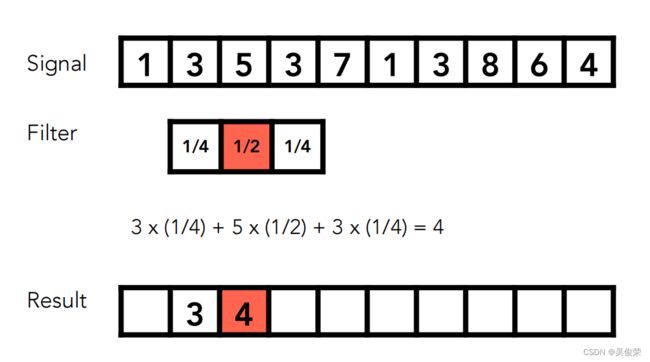
滤波（卷积）
卷积操作：在移动窗口的3个数和信号覆盖的3个数做点乘，结果写回
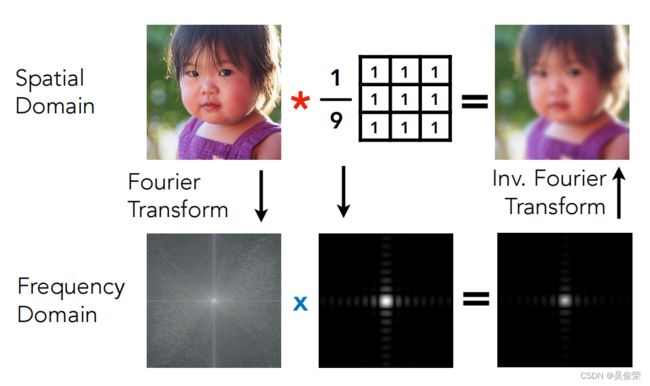
时域上 如果对两个信号进行卷积，其实对应到两个信号各自的频率上是两个信号的乘积，反之亦然
如果把BOX 在时域上变大，那么在频域上反而变小
采样等于重复频率内容
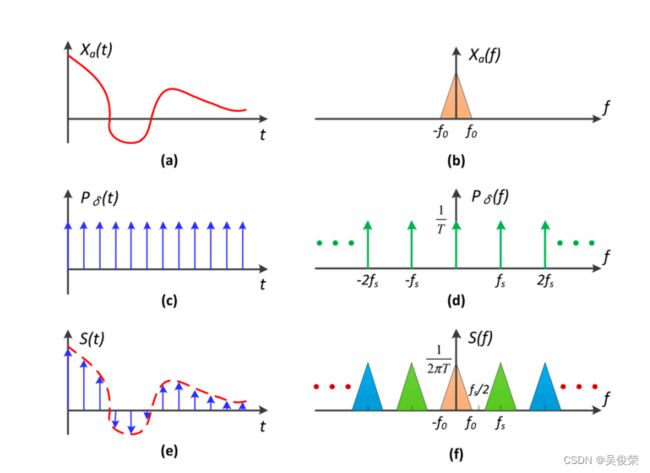
抽样定理的演变。（a） 频带受限信号的时域和（b）频带宽度为f0的频谱；（c） 采样函数的时域信号和（d）重复fs的频谱；（e） 以及（f）分别获得的信号的时域信号和频谱。
在时域上（a）乘积（c）得到 （e）的采样结果
在频域上（b）卷积（d）得到 （f）的采样结果
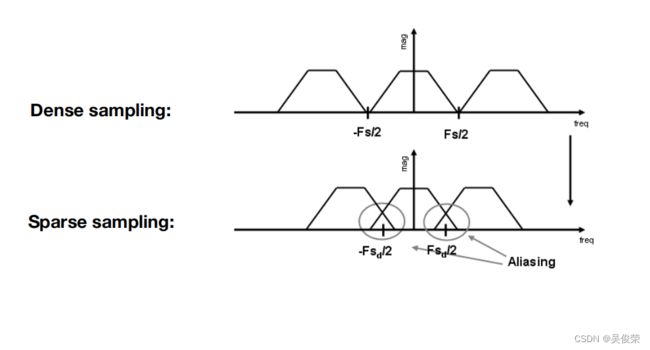
从这看出采样就是重复一个原始信号的频谱
采样不同的的间隔会引起频谱以不同的间隔进行移动
反走样
1.提高采样率
本质上增加了傅立叶域中副本之间的距离
更高分辨率的显示器、传感器、帧缓冲区
但是：成本高昂，可能需要非常高的分辨率
2.消除混叠
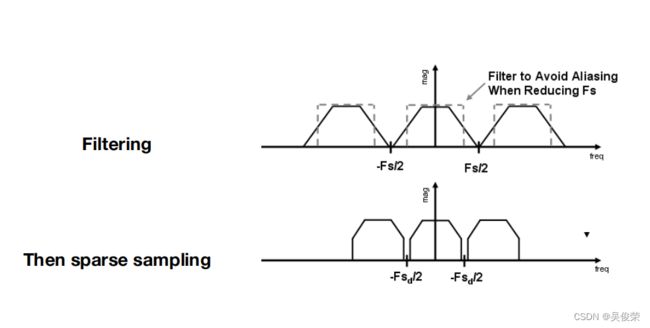
在重复之前使傅立叶内容“变窄”
即在采样前滤除高频
在采样之前为啥先做模糊在采样
就是先把一个信号的高频信息拿掉在采样
解决方案
通过1像素框模糊对f（x，y）进行卷积
卷积=滤波=平均
然后在每个像素的中心进行采样
通过计算平均像素值消除混叠
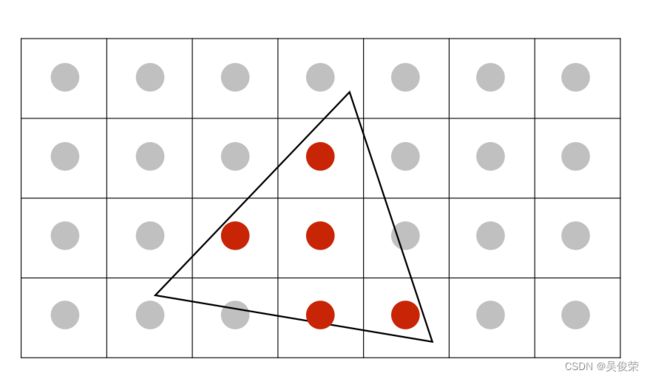
在光栅化一个三角形时，像素内部的平均值
f（x，y）的面积=内侧（三角形，x，y）等于
三角形覆盖的像素。
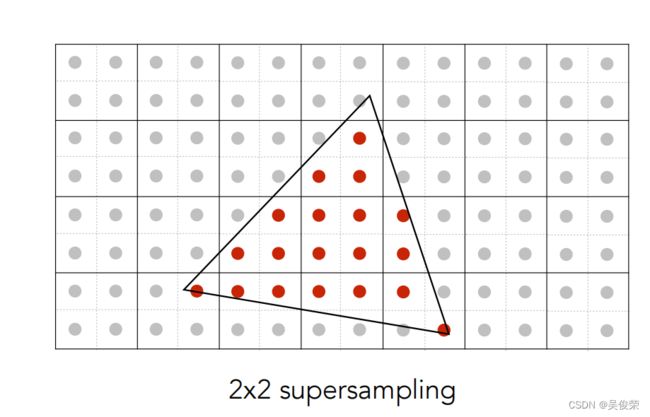
通过超级采样消除混叠（MSAA）
通过对一个像素内的多个位置进行采样并对其值取平均值来近似1像素盒滤波器的效果：
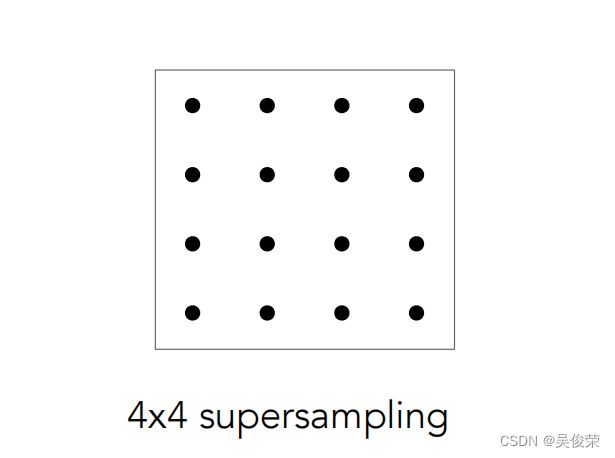
一个像素划分成好多个小的像素，每个小的像素的中心判断是否在 三角型内，然后把这个些像素点平均起来
例子
平均每个像素“内部”的NxN个样本
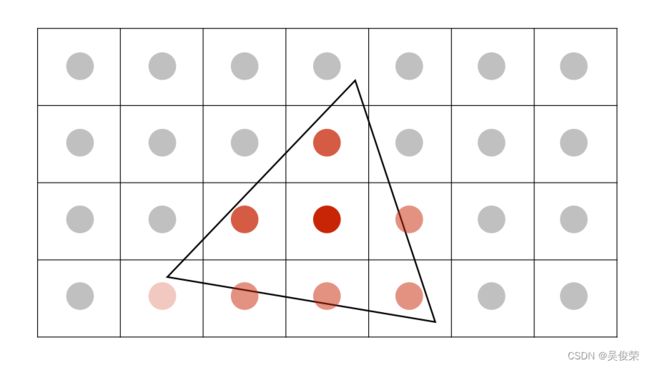
显示器发出的相应信号（对信号模糊）
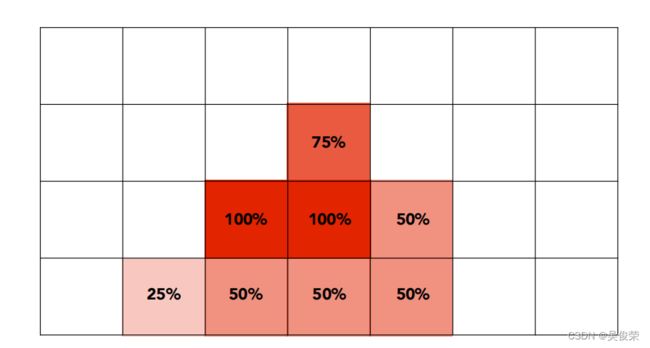
MASS的缺点也很明显增加了很多的采样点
其他的反走样技术
FXAA (Fast Approximate AA)）快速近似抗锯齿 这是一个图像的后期处理，就是通过图像的方便把有锯齿边界找到，并且换成没有锯齿的边界
TAA (Temporal AA) 跟时间相关
一些博客文章
https://zhuanlan.zhihu.com/p/57503957/
https://www.baidu.com/link?url=Qu45xFCB69vvU73K6ldoYovq3eBrzOkekHEMLxGixFEY5TUv2l5D1928Z-MPHzdK&wd=&eqid=f05f1cc0001e4d01000000056430d393
超分辨率/超采样
从低分辨率到高分辨率
本质上仍然存在“样本不足”问题
DLSS（通过深度学习超级采样）