RStan Tuturial

一、介绍

第15章向我们展示了哈密顿蒙特卡罗（HMC）与旧的随机行走大都会和吉布斯算法相比的威力。然而，这种能力是以额外的复杂性为代价的。此外，在HMC中，就像在Random Walk Metropolis中一样，需要调整算法以确保其有效地遍历后验空间。这两个方面可能会使实现HMC成为一种预兆，甚至对于更有经验的MCMCer来说也是如此。幸运的是，对于贝叶斯统计的许多应用，我们不需要：Stan[8]为我们做了艰苦的工作。
Stan实际上实现了HMC的一个改进版本，称为No-U-Turn采样器（NUT），它可以自我调整以获得最大的算法效率。这让stan跑得很快，真的很快。用户所需要做的就是使用直观且易于学习的Stan语言来编写模型，其余的由Stan完成。该语言正在不断更新和改进，使用了一些业内最优秀的人才。特别是，这种语言是世界上最重要的贝叶斯之一Andrew Gelman的创意。
Stan是一种概率建模语言，它实现了黑盒MCMC，可以通过多种接口访问，包括R、Python、命令行、Matlab、Stata、Mathematica和Julia。R接口被称为RStan，可能是其中最流行的。它的流行意味着它得到了很好的测试和支持，因此在本章中，我们提供了使用此包的示例。然而，虽然我们使用RStan来调用Stan，但底层模型始终使用相同的Stan语言编写，这意味着我们在本章中提供的Stan程序示例不会在接口之间发生变化。

二、Write a Stan Program

2.1 Data

data{
real Y[10]; //十个人的身高heights
}

我们宣布变量Y（代表10个人的身高）为实数类型[10]。这意味着它是一个包含10个元素的数组，每个元素都是一个无界连续变量。有一系列不同的数据类型可以声明，这里我们只包括几个示例：

real<lower=0,upper=1> Z;//：在0和1之间有界的连续变量

int<lower=0> Z; //采用最小值为0的整数值的离散变量

int<lower=0> Z[N]; //一个长度为N的数组，其中数组的每个元素都是一个离散变量，该变量采用最小值为0的整数值

vector[N] Z; //长度为N的连续变量向量

matrix[3,3] Z; // 连续变量的3×3矩阵

matrix[3,3] Z[5,2]; //3×3矩阵的5×2数组

在上面的其他类型中，我们介绍了数组、向量和矩阵。你可能想知道这三种类型之间的区别。向量和矩阵只包含实数类型的元素，即连续变量，而数组可以包含任何类型的数据。在上面，我们展示了如何声明整数和矩阵的数组。那么为什么要使用更有限的向量和矩阵类型呢？

1. 首先，它们可以用于线性代数，而数组不能。
2. 其次，一些函数（例如，多元正态分布）使用这些类型作为输入，而不是数组。
3. 第三，由于数据存储在内存中的方式，使用矩阵而不是二维阵列有一些小的内存和速度优势。

2.2 Data

我们考虑的下一部分代码是parameters块，在这里我们声明了我们将在模型中推断的所有参数：

parameters { 
real mu; //样本人群中的身高heights均值

real<lower=0> sigma; // 身高heights的标准差
}

这里，我们声明了样本人群中的平均高度，这是一个无界连续变量，以及标准差，这是连续非负变量。注意，我们可以在这里指定mu的下限为零，因为它必须是非负的；然而，在实践中，接近该界限的参数值是不接近的。
与数据块一样，这里提供了一系列数据类型。其中包括我们之前讨论过的向量、矩阵和数组类型，但也包括更奇特的实体，其中一些实体如下所示：

simplex[K] Z; //K个非负连续变量的向量，其和为1；simplex用于参数向量，其元素表示概率.

corr_matrix[K] Z; //K×K维相关矩阵（具有单位对角线的对称正定矩阵，所有元素在−1和1之间）
ordered[K] Z; //K个连续元素的向量，其中Z[1]>Z[2]>…>Z[K]或Z[1]

注意，上述描述中缺少离散参数。这不是一个错误。Stan目前不支持整数值参数，至少直接不支持。这是因为用于离散参数的HMC理论尚未得到充分发展。然而，Stan开发团队正在进行这项工作，希望在未来的某个时候，这将成为可能。虽然这似乎是一个严重的问题，但由于许多模型包含离散参数，因此可以通过将离散参数边缘化来间接包含离散参数（参见第16.6节）。这意味着使用离散参数的绝大多数模型仍然可以在Stan中编码。

2.3 Model

我们讨论的Stan程序的下一部分是模型代码块，它用于指定模型的可能性和优先级（或者更一般地，用于增加对数概率）：

for (i in 1:10)  {
	y[i]~normal (mu,sigma); //LIkelihood
}
mu ~ normal(1.5,0.1); //mu的prior
sigma~gamma(1,1); //sigma的prior

2.4 Sampling statements

关于上述块，需要注意的一件重要事情是使用了编写的所谓采样语句。“抽样陈述”一词是暗示性的，不能从字面上理解[8]。在上文中，我们对$Y$的各个元素使用了采样声明，因为我们假设每个高度都是从正态采样分布$Y_i\sim N(\mu ,\sigma )$中得出的。类似地，我们假设参数$\mu$和$\sigma$来自正态分布和伽马先验分布。然而，不要认为$Stan$实际上做了这些陈述所暗示的独立抽样。（如果可以的话，我们就不需要首先进行$MCMC$了！如果你不记得为什么会这样，请参阅第12章。）记住$Stan$基本上是在$HMC$上运行的。$HMC$是一种在负对数后验空间中工作的$MCMC$方法。因为总体后验分子是包括似然性和先验性的多个元素的乘积：
$$p(\theta |X)\propto p(X|\theta )\ast p(\theta )=\prod _{i=1}^{N}p(X_i|\theta )\ast p(\theta )$$
这意味着总体对数后验是似然性和先验中每个元素的个体对数概率之和：

$$log[p(\theta |X)]\propto log[p(X|\theta )]+log[p(\theta )]=\sum _{i=1}^{N}log[p(X_i|\theta )]+log[p(\theta )]$$
因此，在HMC中，我们需要做的就是评估每个元素的对数概率，并将它们相加。对于HMC中的每一步，我们都会得到一个µ和σ的新值，因此，需要评估（未归一化的，负的）对数后验密度。因此，在每一步中，Stan都会计算一个新的对数概率，方法是从0开始，每次遇到~语句时递增。因此：

for(i in 1:10){
Y[i]~normal(mu,sigma);
}

将对数概率相加:
$$log[p(Y[i])]\propto -\frac{1}{2}log({\sigma }^2)-(Y[i]-\mu {)}^2/2{\sigma }^2$$
表达上述采样语句的另一种方法是使用另一种Stan表示法：

for(i in 1:10){
target+=normal_lpdf(Y[i]|mu,sigma);
}

它更透明地将目标（保存对数后验的当前值的容器）增加与Y[i]高度处正常密度的对数相对应的对数概率。这里要明确的是，目标语句实际上与~~~ones并不相同，因为目标语句在日志密度中保持任何常数。然而，对于大多数情况，区别并不重要。使用~语句的Stan程序通常更快，但如果您想要模型的实际对数概率，则需要使用目标语句。
为什么我们要强调统计意义和stan语意义之间的区别？这是因为你可能会得到一些错误，你认为这些错误是Stan中的错误，但实际上是由于统计上的解释。从Stan程序中摘录以下内容：

parameters {
real theta;
} model { 
....
theta ~ uniform(0,1);
 }

乍一看，似乎参数θ应该被限制在0和1之间，因为它具有与这些边界连续的先验。然而，事实并非如此。上述所有采样语句都是将对数概率增加对数均匀密度给定的量。这意味着θ有可能偏离0和1的界限，如果您运行这个程序，您可能会在几次迭代中看到这一点。（Stan将输出形式为“Log probability evaluates to Log（0）…”的语句。）

2.5 Vectorisation

实际上，有一种更有效、更紧凑的方法来编写我们的原始模型，它利用了采样语句固有的矢量化特性：

model {
Y ~ normal(mu,sigma); // likelihood
...
}

这里我们已经用上面的替换了单独访问Y的每个元素的for循环，这里我们使用左侧的数组Y。对于更复杂的模型，使用矢量化代码可以大大提高MCMC的速度，因为代码在翻译时能够更好地利用C++的优势。

2.6 Probability distributions

Stan配备了一系列有用的概率分布。我们没有在下面列出所有这些，因为它们很容易在Stan手册中找到，并且不断更新。然而，这里有一些更流行的发行版：

1. 离散：Bernoulli, binomial, Poisson, beta-binomial, negativebinomial, categorical, multinomial
2. 连续无界：normal, skew-normal, Student-t, Cauchy, logistic
3. 连续有界：uniform, beta, log-normal, exponential, gamma, chi-squared, inv-chi-squared, Weibull, Wiener diffusion, Pareto
4. 多变量连续：normal, Student-t, Gaussian process
5. 异国情调Exotics：Dirichlet，LKJ，Wishart和invWishart，Von-Mises
   还值得注意的是，Stan有时会提供相同概率分布的不同参数化（例如，参见Stan手册中的二项式和binomial_logit分布），这会使生活更轻松。

三、 从R执行Stan程序

现在我们了解了Stan程序的上述数据、参数和模型块，让我们讨论如何通过RStan在R中执行Stan程序。请注意，本节假设您已按照第16.4节所述安装了R、RStudio和RStan。要开始并运行，请执行以下步骤：
1.创建一个新文件夹，其中包含.stan文件以及一个R文件，我们将使用该文件来调用stan。

2.在RStudio中创建一个新的文本文件，并将代码块1中的代码粘贴到其中。将此文件保存在新创建的文件夹中，为“simple.stan”（这样做时，您应该看到RStudio突出显示符合stan语法的代码）。

3.在RStudio中创建一个新的R脚本文件，并将其保存在文件夹中。

4.在RStudio中，将工作目录更改为与新创建的文件夹相同。这可以通过窗口顶部的下拉菜单手动完成，也可以使用一行代码来完成，代码如下所示：

library(rstan) 
options(mc.cores = parallel::detectCores())
N<-10
Y<-rnorm(N,1.5,0.2)
hist(Y)
fit <- stan('simple.stan',iter=200,chains = 4,data=list(Y=Y))
print(fit,probs = c(0.25,0.5,0.75))

Stan文件的内容：文件名设置为simple.stan

data {
  real Y[10];
}
parameters{
  real mu;
  real<lower=0>sigma;
}
model{
  for(i in 1:10){
    target+=normal_lpdf(Y[i]|mu,sigma);//likelihood
  }
  mu~normal(1.5,0.1);//prior for mu
  sigma~gamma(1,1);//prior for sigma
}

结果输出：

Inference for Stan model: simple.
4 chains, each with iter=200; warmup=100; thin=1; 
post-warmup draws per chain=100, total post-warmup draws=400.

      mean se_mean   sd  25%  50%  75% n_eff Rhat
mu    1.55    0.00 0.07 1.50 1.55 1.59   374 1.00
sigma 0.32    0.01 0.08 0.26 0.31 0.36   157 1.02
lp__  5.48    0.06 0.89 5.11 5.78 6.10   189 1.00

Samples were drawn using NUTS(diag_e) at Mon Mar  6 16:21:22 2023.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

那么，上述输出的结果是什么意思呢？上面的部分只是说明了四个链每个运行200次迭代。然而，这些链的前半部分被丢弃为“预热”（见第13.9.5节），这意味着每个链只有100个样本作为后样本，导致400=4×100“预热后总抽取量”。
输出中的表包含我们模型的两个参数（µ，σ）以及模型“lp__”的对数概率的和统计信息。
表的最后两列是每个参数的收敛诊断：n_eff是有效样本数$Rhat=\hat{R}$;
在本例中，我们看到，对于所有参数，$\hat{R}<1.1$给了我们一些信心，即如果我们收集更多样本，我们的后验形状不会发生很大变化。表的前六列显示了后验样本的汇总度量，包括均值（及其标准误差）、标准差和我们在print（fit，probs=c（0.25,0.5,0.75））语句中指定的三个分位数。输出的最后一部分包含关于每个链所使用的采样算法（NUT）和估计的贝叶斯缺失信息分数（BFMI）的信息。BFMI是一个新创建的标准，它测量每个链采样的能量分布的自相关，值接近1表示有效采样[4]。
n_ eff是有效样本大小的粗略度量，
Rhat是分裂链上的潜在规模缩减因子（收敛时，Rhat=1）

3.1 提取后验样本&绘制图表

library(ggplot2)
mu <- extract(fit,'mu')[[1]]
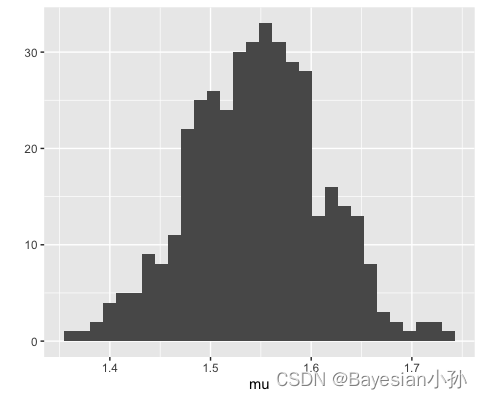
qplot(mu)

输出结果：

其中$extract$是一个$RStan$函数，它从$Stan-fit$对象中提取我们想要的任何参数。我们选择使用“$ggplot2$”库在此处显示数据的直方图。

3.2、$shinyStan$

如果您使用的是$R$，那么还有另一种更具交互性（因此也更有趣）的方法来查看$Stan$运行的结果，使用$shinyStan$包。您可以使用以下方法从$R$中安装此软件包：

install.packages('shinystan')

创建$shinyStan$对象并启动$shinyStan$应用程序很简单：

library(shinystan)
aFit <- as.shinystan(fit)
launch_shinystan(aFit)

执行上述操作后，您的网络浏览器将打开（您不需要连接到$Internet$），您将看到一个包含DIAGNOSE、ESTIMATE和EXPLORE选项的介绍屏幕。DIAGNOSE允许您通过单击查看详细的MCMC诊断标准各种选项，包括收敛标准，如$\hat{R}$、有效样本大小和发散迭代。
ESTIMATE提供了模型中参数的表格和基本图表。
EXPLORE，除其他外，允许您创建每个变量的样本散点图。该图尤其适用于诊断MCMC问题（参见第16.7.2节）。

3.3其他块

到目前为止，我们介绍的三个代码块在Stan程序中通常是必不可少的（反例见第16.6节）；然而，还有其他代码块可以帮助生活变得更加轻松。在本节中，我们将描述这些。

3.3.1 生成的数量

其他块中最广泛使用的是生成数量/Generated quantities代码块。本节的主要用途之一是对模型的拟合进行后验预测检查（见第10章）。一旦你了解了这一部分的工作原理，你会发现在这里进行后验预测检查要比在R、Python等中进行后验检查容易得多。Stan程序的这一部分每个样本执行一次，这意味着它通常不会对效率造成威胁（尽管它会显著影响Stan使用的内存；请参见第16.5.5节）。
让我们使用前面章节中的heights示例来说明如何使用此代码块进行后验预测检查。假设我们想测试我们的模型是否能够生成我们在数据中看到的极端值。特别是，我们选择计算后验预测样本的分数——每个样本的大小与原始数据相同——其中模拟数据的最大值或最小值比实际数据更极端。我们使用如下代码：

generated quantities{
	vector[10] lSimData;
	int aMax_indicator;
	int aMin_indicator;
	
	// Generated posterior predictive samples
	for(i in 1:10) {
		lSimData[i] = normal_rng(mu,sigma);
	}
	// Compare with real data
	aMax_indictor = max(lSimData) > max(Y);
	aMin_indictor = min(lSimData) < min(Y);
}

这段代码的第一部分只是声明了我们打算在这个块中使用的变量。然后，我们使用μ和σ的后验样本生成与实际数据长度相同的后验预测样本。然后，我们确定模拟数据的最大值和最小值是否比真实数据更极端，如果是这种情况，则生成一个等于1的变量，否则为0。

注意，为了从给定分布生成随机样本，我们使用“_rng”后缀。因此，在上文中，$Y=norma{l}_{r}ng（\mu ，sigma）$从具有μ均值和sigma标准偏差的正态分布生成单个（伪）独立样本。这与$Y\sim Norm(\mu ,\sigma )$完全不同，这意味着“将总对数概率增加一个量，该量由正态分布的数据点Y的对数似然给出，平均值为μ，标准偏差为sigma”（如果需要提醒自己，请参见第16.5.1节）。
如果我们运行整个程序，包括底部的生成数量部分，我们将获得如下结果：

library(rstan) 
options(mc.cores = parallel::detectCores())
N<-10
Y<-rnorm(N,1.5,0.2)
hist(Y)
fit <- stan('simple.stan',iter=200,chains = 4,data=list(Y=Y))
# print(fit,probs = c(0.25,0.5,0.75))
# library(ggplot2)
#mu <- extract(fit,'mu')[[1]]
#qplot(mu)
#install.packages('shinystan')
#library(shinystan)
#aFit <- as.shinystan(fit)
#launch_shinystan(aFit)
print(fit,probs = c(0.25,0.5,0.75))

输出结果为：

Inference for Stan model: simple.
4 chains, each with iter=200; warmup=100; thin=1; 
post-warmup draws per chain=100, total post-warmup draws=400.

                mean se_mean   sd   25%   50%   75% n_eff Rhat
mu              1.59    0.00 0.06  1.55  1.59  1.63   277 1.00
sigma           0.24    0.01 0.08  0.18  0.21  0.27    76 1.04
lSimData[1]     1.57    0.01 0.25  1.43  1.58  1.73   322 1.00
lSimData[2]     1.59    0.01 0.25  1.45  1.60  1.75   480 1.00
lSimData[3]     1.59    0.01 0.27  1.43  1.61  1.76   422 1.00
lSimData[4]     1.59    0.01 0.25  1.43  1.58  1.73   340 1.01
lSimData[5]     1.56    0.01 0.25  1.41  1.58  1.71   395 1.00
lSimData[6]     1.59    0.02 0.28  1.44  1.59  1.76   335 1.00
lSimData[7]     1.61    0.01 0.24  1.49  1.62  1.74   394 0.99
lSimData[8]     1.59    0.01 0.26  1.43  1.60  1.77   325 1.01
lSimData[9]     1.59    0.01 0.24  1.47  1.61  1.72   281 1.00
lSimData[10]    1.59    0.01 0.25  1.46  1.59  1.74   393 1.00
aMax_indicator  0.42    0.03 0.49  0.00  0.00  1.00   333 1.00
aMin_indicator  0.65    0.03 0.48  0.00  1.00  1.00   284 1.00
lp__           -1.00    0.13 1.26 -1.34 -0.58 -0.16    95 1.03

Samples were drawn using NUTS(diag_e) at Mon Mar  6 21:22:01 2023.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

所以我们现在有了后验预测数据的汇总统计数据。特别是，我们有代表贝叶斯p值的两个指标变量的均值（见第10章）。因此，使用这种后验预测检验，我们得出结论，我们的模型是对数据的合理拟合，因为p值（指标变量样本的平均值）不接近0或1。
此代码块的另一个用途是生成用于测量模型预测性能的必要数据。然而，我们将讨论如何做到这一点，直到第16.6节。
最后，我们将提及但现在不讨论的另一个用途是，生成的数量块可以用于从我们感兴趣的参数中生成样本，这些参数在分层模型的给定级别（参见第17章）。

3.3.2 Functions

如果我们定义函数来执行任何经常使用的操作，代码就可以变得更易读，更不容易出错。作为一个例子，假设我们的样本中的个体的身高，也有他们的体重。假设我们认为这两个变量之间的关系的合理模型可以通过以下方式描述：$Y_i\sim N(\beta log(X_i),\sigma )$
其中$(X_i,Y_i)$是个体i的体重和身高。虽然此模型没有重复，但我们可能会发现使用计算正常值平均值的函数更为方便：

functions{
real covariateMean(real aX, real aBeta){
return(aBeta * log(aX));
}
}

其中函数名前的第一个实数声明函数将返回一个连续变量。
括号中包含的元素告诉函数，它将接受两个实数（aX和aBeta）作为输入。然后，return语句返回所需的值。
注意，可以在Stan函数中声明变量；这里，因为函数很简单，我们选择计算值并在单行中返回。
整个Stan程序的形式如下：

functions{
  real covariateMean(real aX,real aBeta){
    return(aBeta*log(aX));
  }
}
data {
  int N;     // Number of people in sample
  real Y[N]; // Heights for N peoples
  real X[N]; // Weights for N people
}
parameters {
  real beta;
  real<lower=0> sigma; // sd of pop distribution
}
model {
  for(i in 1:N){
    Y[i] ~ normal(covariateMean(X[i],beta),sigma);
  }
  beta ~ normal(0,1);
  sigma ~ gamma(1,1);
}

我们给$\beta \sim N(0,1)$先验，给$\sigma \sim \Gamma (0,1)$先验。
注意，我们选择将样本大小N作为数据传递给Stan程序。这是一个很好的实践，因为它可以将模型推广到更大的样本，否则只会整理事情。还要注意，函数必须在Stan程序的顶部声明，否则其他块在执行时无法找到所需的函数。如果您将此文件保存在工作目录中（再次确保将其保存为.stan），则可以将其进行试驾。为此，在R中生成一些伪数据，然后调用Stan：

N <- 100 
X <- rnorm(N,60,10) 
beta <- 0.3 
sigma <- 0.3 
Y <- beta * log(X) + rnorm(N,0,sigma) 
## Call Stan
fit <-stan('simple_2.stan',iter=200,chains=4,data=list(Y=Y,X=X,N=N))
print(fit,probs = c(0.25,0.5,0.75))

输出结果为：

Inference for Stan model: simple_2.
4 chains, each with iter=200; warmup=100; thin=1; 
post-warmup draws per chain=100, total post-warmup draws=400.

       mean se_mean   sd   25%   50%   75% n_eff Rhat
beta   0.30    0.00 0.01  0.30  0.30  0.31   452 0.99
sigma  0.36    0.00 0.03  0.33  0.35  0.38    79 1.04
lp__  53.87    0.12 1.15 53.29 54.25 54.71    90 1.05

Samples were drawn using NUTS(diag_e) at Mon Mar  6 21:52:15 2023.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

希望你得到的后验样本的均值非常接近用于生成假数据的真实值.

除了帮助您创建更透明、更可靠的代码之外，函数还有另一个用途——它们可以用于从日志密度可以用Stan代码编写的任何分布中进行采样。因此，即使Stan没有特定发行版的内置功能，您仍然可以使用Stan从中进行采样。请参阅第16.6节了解这种神奇药水的配方。

3.3.3 转换的参数

有时，我们希望为参数块中定义的参数的转换生成样本，甚至可能从这些转换后的参数生成样本。在我们最初的高度示例（无协变量）中，假设您不希望在标准偏差参数（sigma）上设置prior，而是希望在方差上设置prior。然而，您还需要为$\sigma$生成样本。一种方法是使用转换后的参数块：