通俗理解机器学习——K-means++ 聚类算法

为什么要使用K-means++ 聚类算法

由于 K-means 算法的结果会受到初始点的选取而有所区别，即K-Means在初始化聚类中心时是在最小值和最大值之间随机取一个值作为其聚类中心，这样的随机取值会导致聚类中心可能选择的不好，最终对结果会产生很大的影响。经过测试，如果样本类别区分度较明显，按照K-Means初始化聚类中心，对结果的影响并不大；反之，如果样本的类别区分度不大，聚类结果会有较大的不同。引用“西瓜书”的相关内容：

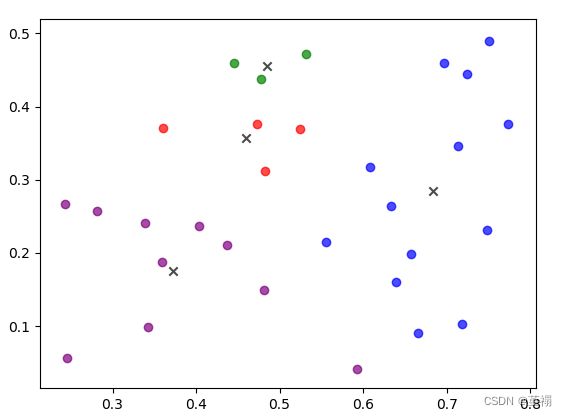
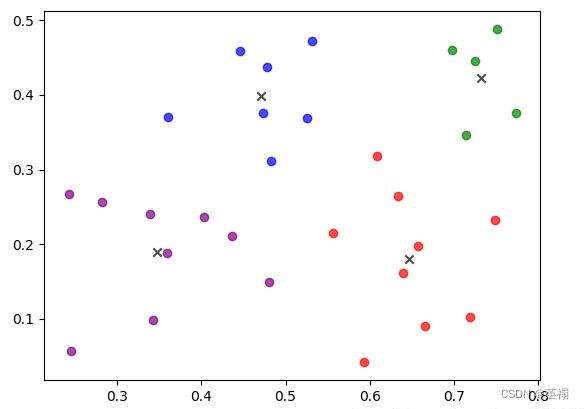
上述两张图可以说明，对于同一数据集，不同的初始聚类中心其产生的结果会有较大的不同。因此提出这种算法的改进: K-Means++算法。

K-Means++算法选择初始聚类中心的基本原则是：初始的聚类中心之间的相互距离要尽可能的远。

K-means 算法步骤

1. 随机初始化k个点作为簇质心；
2. 将样本集中的每个点分配到一个簇：
   计算每个点与质心之间的距离（常用欧式距离和余弦距离），并将其分配给距离最近的质心所对应的簇中
3. 更新簇的质心：
   每个簇的质心更新为该簇所有点的平均值
4. 反复迭代步骤2-3，如果新的质心和以前的质心距离小于一定的阈值，可以认为我们进行的聚类算法已经达到期望的结果，算法终止，反之继续迭代。

K-means++ 算法步骤

1. 从数据集中随机选择一个点作为第一个聚类中心
2. 计算每个样本与当前已有聚类中心之间的最短距离D(x)，即与最近的一个聚类中心的距离（以概率选择距离最大的样本作为新的聚类中心）。这个值越大，表示被选取作为聚类中心的概率较大；并计算每个样本被选为下一个聚类中心的概率（如下所示），最后用轮盘法选出下一个聚类中心。
   
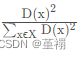
3. 重复过程（2）直到找到k个聚类中心。

选出初始点后，就继续使用标准的 K-Means算法（上述） 中第2步到第4步了。

实例

通过例子说明K-means++是如何选取初始聚类中心的。数据集中共有8个样本，分布以及对应序号如下图所示：

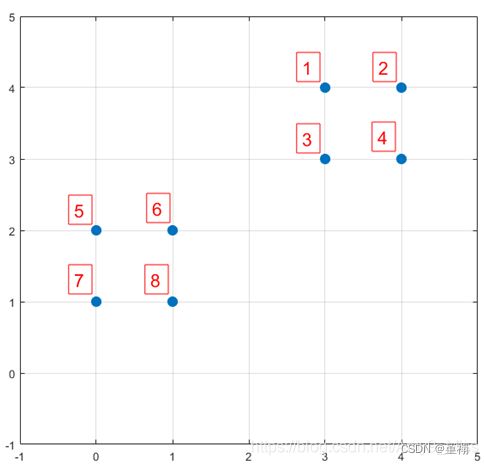
假设经过K-means++步骤1后，6号点(1, 2)被选择为第一个初始聚类中心，那在进行步骤二时每个样本的D(x)和被选择为第二个聚类中心的概率如下表所示：

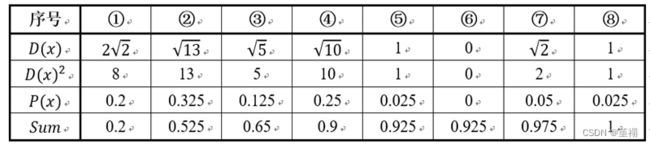
其中的P(x)就是每个样本被选为下一个聚类中心的概率。最后一行的Sum是概率P(x)的累加和。

用轮盘法选择出第二个聚类中心：方法是随机产生出一个[0, 1]之间的随机数，判断它属于哪个区间，那么该区间对应的序号就是被选择出来的第二个聚类中心了。例如1号点的区间为[0,0.2]，2号点的区间为(0.2, 0.525]等等。 如果给出的随机数是0.45，那么2号就是第二个聚类中心了。

从上表可以直观的看到第二个初始聚类中心是1号，2号，3号，4号中的一个，因为这四个点的累计概率为0.9，占了很大一部分比例。而从上图中也可以看到，这4个点正好是离第一个初始聚类中心6号点较远的四个点。

这也验证了K-means的改进思想：即离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。

Python代码实现

import time
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

def distEclud(vecA,vecB):
    """
    计算两个向量的欧式距离
    """
    return np.sqrt(np.sum(np.power(vecA-vecB,2)))

def get_closest_dist(point, centroids):
    """
    计算样本点与当前已有聚类中心之间的最短距离
    """
    min_dist = np.inf  # 初始设为无穷大
    for i, centroid in enumerate(centroids):
        dist = distEclud(np.array(centroid), np.array(point))
        if dist < min_dist:
            min_dist = dist
    return min_dist

def RWS(P, r):
    """利用轮盘法选择下一个聚类中心"""
    q = 0  # 累计概率
    for i in range(len(P)):
        q += P[i]  # P[i]表示第i个个体被选中的概率
        if i == (len(P) - 1):  # 对于由于概率计算导致累计概率和小于1的，设置为1
            q = 1
        if r <= q:  # 产生的随机数在m~m+P[i]间则认为选中了i
            return i

def getCent(dataSet, k):
    """
    按K-Means++算法生成k个点作为质心
    """
    n = dataSet.shape[1]  # 获取数据的维度
    m = dataSet.shape[0]  # 获取数据的数量
    centroids = np.mat(np.zeros((k, n)))
    # 1. 随机选出一个样本点作为第一个聚类中心
    index = np.random.randint(0, n, size=1)
    centroids[0, :] = dataSet[index, :]
    d = np.mat(np.zeros((m, 1)))  # 初始化D(x)
    for j in range(1, k):
        # 2. 计算D(x)
        for i in range(m):
            d[i, 0] = get_closest_dist(dataSet[i], centroids)  # 与最近一个聚类中心的距离
        # 3. 计算概率
        P = np.square(d) / np.square(d).sum()
        r = np.random.random()  # r为0至1的随机数
        choiced_index = RWS(P, r)  # 利用轮盘法选择下一个聚类中心
        centroids[j, :] = dataSet[choiced_index]
    return centroids

def kMeans_plus2(dataSet,k,distMeas=distEclud):
    """
    k-Means++聚类算法,返回最终的k各质心和点的分配结果
    """
    m = dataSet.shape[0]  #获取样本数量
    # 构建一个簇分配结果矩阵，共两列，第一列为样本所属的簇类值，第二列为样本到簇质心的误差
    clusterAssment = np.mat(np.zeros((m,2)))
    # 1. 初始化k个质心
    centroids = getCent(dataSet,k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            minDist = np.inf
            minIndex = -1
            # 2. 找出最近的质心
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            # 3. 更新每一行样本所属的簇
            if clusterAssment[i,0] != minIndex:
                clusterChanged = True
            clusterAssment[i,:]=minIndex,minDist**2
        print(centroids) # 打印质心
        # 4. 更新质心
        for cent in range(k):
            ptsClust = dataSet[np.nonzero(clusterAssment[:,0].A==cent)[0]] # 获取给定簇的所有点
            centroids[cent,:] = np.mean(ptsClust,axis=0) # 沿矩阵列的方向求均值
    return centroids,clusterAssment

def plotResult(myCentroids,clustAssing,X):
    """将结果用图展示出来"""
    centroids = myCentroids.A  # 将matrix转换为ndarray类型
    # 获取聚类后的样本所属的簇值，将matrix转换为ndarray
    y_kmeans = clustAssing[:, 0].A[:, 0]
    # 未聚类前的数据分布
    plt.subplot(121)
    plt.scatter(X[:, 0], X[:, 1], s=50)
    plt.title("未聚类前的数据分布")
    plt.subplots_adjust(wspace=0.5)

    plt.subplot(122)
    plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
    plt.scatter(centroids[:, 0], centroids[:, 1], c='red', s=100, alpha=0.5)
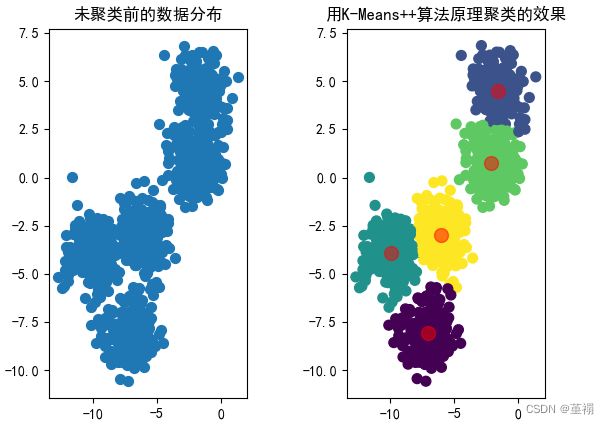
    plt.title("用K-Means++算法原理聚类的效果")
    plt.show()
    
def load_data_make_blobs():
    """
    生成模拟数据
    """
    from sklearn.datasets import make_blobs  # 导入产生模拟数据的方法
    k = 5  # 给定聚类数量
    X, Y = make_blobs(n_samples=1000, n_features=2, centers=k, random_state=1)
    return X,k

if __name__ == '__main__':
    X, k=load_data_make_blobs()  # 获取模拟数据和聚类数量
    s = time.time()
    myCentroids, clustAssing = kMeans_plus2(X, k, distMeas=distEclud) # myCentroids为簇质心
    print("用K-Means++算法原理聚类耗时：", time.time() - s)
    plotResult(myCentroids, clustAssing, X)

运行结果如下：

总结

• K-Means++算法选择初始聚类中心的基本原则是：初始的聚类中心之间的相互距离要尽可能的远。这个改进虽然直观简单，但是却非常得有效。
• 缺点：由于聚类中心点选择过程中的内在有序性，在扩展方面存在着性能方面的问题(第k个聚类中心点的选择依赖前k-1个聚类中心点的值)。

相关链接

轮盘选择法