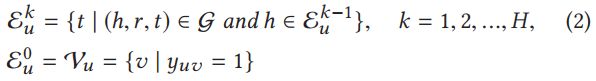RippleNet详解(上)：论文详解
RippleNet详解(上)：论文详解
1. 前言
已经很久没有更新博客了，看了一些博客已经被几百赞了，有了一些动力，这一段时间也积累了很多包括论文、代码、技巧等相关经验，后续会陆续更新。
RippleNet详解主要分为两个系列——论文详解和代码详解，这个博客首先对论文进行一些解释。首先呈上论文了链接：Rippleset论文链接(arxiv)
2. 简介
将知识图谱(Knowledge Graph, KG)引入推荐系统(Recommender Systems, RS)主要有三个作用：
- 缓解冷启动
- 缓解数据稀疏
- 可解释性
RippleNet就是基于KG的推荐算法，其目的也是尝试解决以上三个问题。
首先要说明RippleNet的一些特点：
- RippleNet使用的KG是item graph。何为item-graph？放在KG中作为实体的主要有用户(user)、商品(item)和属性(attribute)。KG中如果包含三者，则称之为user-item graph，如果KG中只包含item和attribute，则称之为item graph。参见KG for RS综述(arxiv)
- RippleNet是Unified Method。利用KG边信息的RS主要分为三类，第一类是基于Path-based Method，如Meta Path；第二类是基于embedding的，如CKE；第三类就是综合第一类和第二类，称为Unified Method。
- RippleNet借鉴了GraphSage的思想。RippleNet将用户点击的结点作为源点，像水波纹一样向周围扩展，吸收1-hop和2-hop的信息，实现消息传递。
- RippleNet为CTR设计。评估指标是AUC和ACC。
3. 公式分析
3.1 用户商品交互矩阵 和 预测目标：
（1）用户商品交互矩阵：
这个很好理解，比如用户点击、收藏或下单的商品，设置为1，否则为0。
（2）预测目标：
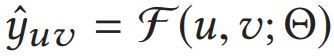
y ^ u v 是 用 户 u 点 击 v 的 概 率 ; Θ 包 含 所 有 实 体 、 关 系 的 e m b e d d i n g s \hat{y}_{uv}是用户u点击v的概率;\Theta 包含所有实体、关系的embeddings y^uv是用户u点击v的概率;Θ包含所有实体、关系的embeddings
3.2 RippleSet创建：
在介绍RippleSet前，我们先说一个基本概念：
（1）相关实体集
可以看到这是实体的集合，比如：
- k=0，表示用户点击的商品序列
- k=1，表示以用户点击的商品序列为头实体的三元组的尾实体；
- 其他情况以此类推，我们可以想象 ε u k \varepsilon_{u}^{k} εuk就是第k个波纹上的实体。
（2）RippleSet
在论文中的定义：
看着是不是十分复杂？
对比一下 S u k S_{u}^{k} Suk和 ε u k \varepsilon_{u}^{k} εuk，我们会发现，除了 S u k S_{u}^{k} Suk表示三元组， ε u k \varepsilon_{u}^{k} εuk表示实体外，两者是没有区别的。因此，我们可以理解 S u k S_{u}^{k} Suk就是第k-1个波纹为头实体，第k个波纹为尾实体的三元组集合。
RippleSet是核心数据，根据用户点击的商品，在KG上生成与商品相关的实体集合。用C++模板的表示方式就是：
dict,list,list),
tuple(list,list,list)>>
这是2-hop的表示，因此最外层list中有两个tuple，分别表示1-hop和2-hop；tuple中的3个list是等长的，分别表示头实体，关系，尾实体。
为什么“等长”会加粗呢？给你三秒钟思考时间：
3
2
1
因为采用了固定大小的邻居采样呀。虽然每个节点的邻居不一样，但是每次采样都采样固定大小的邻居，比如采样16个邻居。如果邻居少于16个，怎么办？重采样呗。你可能好奇我是肿么知道的，因为我看了代码。
3.3 偏好传播：
把邻居采样好以后，就是如何吸收邻居的信息，在GCN中叫做消息传递，在RS里，我们称之为偏好传播，其目的是求出用户的embeddings。
先看论文公式（4）：
简单来说， V ∈ R d V\in \mathbb{R}^{d} V∈Rd表示用户点击的商品， h i h_{i} hi表示 V V V的1-hop邻居， R i R_{i} Ri是它们之间的关系。 p i p_{i} pi就是两者的归一化相似度。
因此用户的1-hop表示为不同邻居节点的attention之和：
向外传播的2-hop的用户表示 o u 2 o_{u}^{2} ou2可以用同样的方法求得。
用户最终的表示为各hop表示之和：
论文中采用的是2-hop，也就是：
在获得用户表示 u u u之后，用户点击商品的概率通过其內积的sigmoid函数来计算，这是很通用的做法，不需要太多的解释吧。
3.4 如何学习模型：
作者在论文中洋洋洒洒写了一堆公式，咋一看一脸懵逼，其实就是条件概率链式法则，具体如何链式，可参见花书3.6 花书介绍。下面我直接解释论文。
RippleNet的目的是在已知KG G \mathcal{G} G 和交互矩阵 Y Y Y的条件下，最大化参数 Θ \Theta Θ后验概率。再次说明一遍， Θ \Theta Θ可以理解为所有实体和关系的embeddings。
公式(8)是最大后验估计(MAP)，理论上MAX应该改为argmax，即最大化在给定数据样本的情况下模型参数的后验概率。（2021.4.13）
根据贝叶斯理论和花书3.6链式法则，（8）可以转化为：
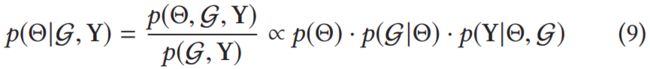
即与：
- 模型参数 Θ \Theta Θ的先验概率 p ( Θ ) p(\Theta) p(Θ)、
- 给定 Θ \Theta Θ的条件下，观察到KG G \mathcal{G} G 的概率 p ( G ∣ Θ ) p(\mathcal{G}|\Theta) p(G∣Θ)以及
- 给定 Θ \Theta Θ和KG G \mathcal{G} G的观测隐式反馈Y的似然函数 p ( Y ∣ Θ , G ) p(Y|\Theta,\mathcal{G}) p(Y∣Θ,G)
成正比。
对于第一项 p ( Θ ) p(\Theta) p(Θ)，因为我们不知道 Θ \Theta Θ的真实分布，因此，作者假设 Θ \Theta Θ为高斯分布，所以：
对于第二项 p ( G ∣ Θ ) p(\mathcal{G}|\Theta) p(G∣Θ)，可以用KGE来表示KG，RippleNet借鉴了语义匹配模型来表示KGE。因此 p ( G ∣ Θ ) p(\mathcal{G}|\Theta) p(G∣Θ)可以转化为每个事实的概率乘积，如（11）第一行，之后通过设置超参 λ 2 \lambda _{2} λ2作为方差， I h , r , t I_{h,r,t} Ih,r,t为指示函数((h,r,t为事实则为1否则为0))来增加事实的概率，可得下式：
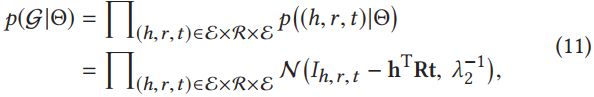
对于第三项 p ( Y ∣ Θ , G ) p(Y|\Theta,\mathcal{G}) p(Y∣Θ,G)，由于 Y Y Y的取值只有0,1，并且正例的概率为 σ ( u T v ) \sigma (u^{T}v) σ(uTv),对于一个样例， P = σ ( u T v ) y u v ⋅ ( 1 − σ ( u T v ) ) 1 − y u v P = {\sigma (u^{T}v)}^{y_{uv}} {\cdot}(1-{\sigma}(u^{T}v))^{1-y_{uv}} P=σ(uTv)yuv⋅(1−σ(uTv))1−yuv，对于所有的评分，有：
综上，损失函数为：
注意，高斯分布取log就会变成以上平方形式。
3. 总结
以上，就是RippleNet的全部内容，后续会更新RippleNet代码解析。
完。