每日一练28&&29——反转部分单向链表&&猴子分桃&&求正数数组的最小不可组成和（难）&&有假币

---

反转部分单向链表

题目链接：

方法一：

常规思路：找到需要反转部分链表的起始位置,断链反转之后,再进行恢复链表输出。

代码：

# include 
using namespace std;
struct list_node {
    int val;
    struct list_node* next;
};
list_node* input_list(void) {
    int n, val;
    list_node* phead = new list_node();
    list_node* cur_pnode = phead;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &val);
        if (i == 1) {
            cur_pnode->val = val;
            cur_pnode->next = NULL;
        } else {
            list_node* new_pnode = new list_node();
            new_pnode->val = val;
            new_pnode->next = NULL;
            cur_pnode->next = new_pnode;
            cur_pnode = new_pnode;
        }
    }
    return phead;
}


list_node* ReverseList(list_node* head) {
    list_node* prev = nullptr, *cur = head;
    while (cur) {
        list_node* next = cur->next;
        cur->next = prev;
        prev = cur;
        cur = next;
    }
    return prev;
}
list_node* reverse_list(list_node* head, int L, int R) {
    list_node* newHead = new list_node;
    newHead->next = head;
    list_node* prevNode = newHead, *RHead = nullptr, *RTail = nullptr,
               *TailNext = nullptr;
    for (int i = 0; i < L - 1; i++) {
        prevNode = prevNode->next;
    }
    RHead = prevNode->next;
    RTail = RHead;
    for (int i = 0; i < R - L; i++) {
        RTail = RTail->next;
    }
    TailNext = RTail->next;
    RTail->next = nullptr;
    list_node* RNewHead = ReverseList(RHead);
    prevNode->next = RNewHead;
    RHead->next = TailNext;
    return newHead->next;

}
void print_list(list_node* head) {
    while (head != NULL) {
        printf("%d ", head->val);
        head = head->next;
    }
    puts("");
}

int main () {
    int L, R;
    list_node* head = input_list();
    scanf("%d%d", &L, &R);
    list_node* new_head = reverse_list(head, L, R);
    print_list(new_head);
    return 0;
}

方法二：

方法一的弊端:假设需要反转的链表部分,占比比较大,则需要两次遍历链表来实现.
(第一遍遍历确定反转链表的起始位置，第二遍遍历链表进行反转).
那是不是可以考虑一次遍历链表就解决该问题呢?
这里的思路是:采用头插的方式一次遍历解决问题

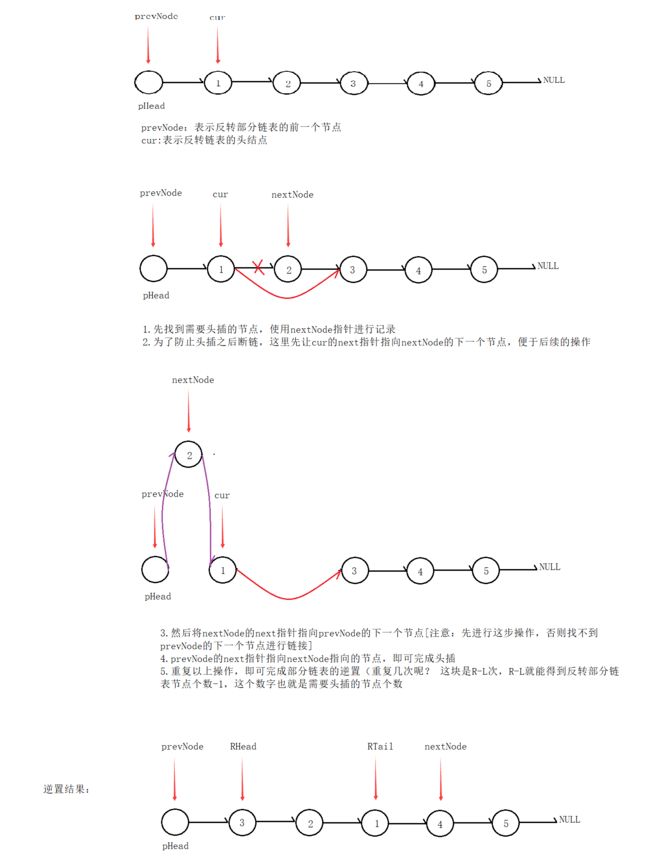
代码：

# include 
using namespace std;
struct list_node {
    int val;
    struct list_node* next;
};
list_node* input_list(void) {
    int n, val;
    list_node* phead = new list_node();
    list_node* cur_pnode = phead;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &val);
        if (i == 1) {
            cur_pnode->val = val;
            cur_pnode->next = NULL;
        } else {
            list_node* new_pnode = new list_node();
            new_pnode->val = val;
            new_pnode->next = NULL;
            cur_pnode->next = new_pnode;
            cur_pnode = new_pnode;
        }
    }
    return phead;
}

list_node* reverse_list(list_node* head, int L, int R) {
//在下面完成代码

    list_node* pHead = new list_node;
    pHead->next = head;
    list_node* prevNode = pHead;
    for (int i = 0; i < L - 1; i++) {
        prevNode = prevNode->next;
    }
    list_node* cur = prevNode->next;
    for (int i = 0; i < R - L; i++) {
        list_node* nextNode = cur->next;
        cur->next = nextNode->next;
        nextNode->next = prevNode->next;
        prevNode->next = nextNode;
    }
    list_node* list = pHead->next;
    free(pHead);
    return list;

}

void print_list(list_node* head) {
    while (head != NULL) {
        printf("%d ", head->val);
        head = head->next;
    }
    puts("");
}

int main () {
    int L, R;
    list_node* head = input_list();
    scanf("%d%d", &L, &R);
    list_node* new_head = reverse_list(head, L, R);
    print_list(new_head);
    return 0;
}

---

猴子分桃

题目链接：

思路：

当n=3，即有三只小猴子时，设总共有x个桃子
递推步骤如下：

     		可以分得桃子数量             		       剩余的桃子数量
第一个小猴子，（x-1）* 1/5                     （x-1）* 4/5=4/5x-4/5
第二个小猴子，（（x-1）*4/5-1）*1/5       （4/5x-4/5-1）*4/5=（4/5）^2*x -（4/5)^2-(4/5)
第三个小猴子，（（4/5x-4/5-1）*4/5-1）*1/5  （（4/5）2*x-（4/5）^2-4/5-1）*4/5
  										（（4/5）^3*x-（4/5）^3-（4/5）^2-4/5）

那么剩余的桃子数量的通式就是：
（（4/5)^n*x -（（4/5)^n+（4/5)^(n-1)+...+（4/5）^1）

设S =（4/5)^n+（4/5)^(n-1)+...+（4/5)^1
4/5S=（4/5)^(n+1)+（4/5)^n+...+（4/5)^2
S-4/5S=1/5S=4/5 -（4/5）^(n+1)
           =4/5*（1-（4/5）^n）
S=4*(1-（4/5）^n）

然后把S再带回去

（4/5）^n*x - 4*（1-4/5^n)

（4/5)^n*x - 4+4*（4/5）^n
（4/5)^n *（x+4）-4
通式最后就被化解为：4^n/5^n*（x+4)-4
题目说 老猴子最少能得到几个桃子？
最小的情况：
（x+4)=5^n
x=5^n-4
--------------所以最少需要有5^n-4个桃子。----------------


老猴子最终最小剩余的数量=分完剩余+n
（4/5)^n*（x+4）-4
（4/5）^n*（5^n-4+4)-4
（4/5）^n*（5^n）-4
 4^n/5^n*(5^n)-4


 剩余的桃子数量:4^n-4
---------------- 老猴子分得的桃子:4^n-4+n------------
 

代码：

#include 
#include 
#include 
int main() {
    int n;
    while (std::cin >> n) {
        if (n == 0) break;
        long total = pow(5, n) - 4;
        long left = pow(4, n) + n - 4;
        std::cout << total << " " << left << std::endl;
    }
    return 0;
}

---

求正数数组的最小不可组成和

题目链接：

思路：

这是一个动态规划的01背包问题；
根据承重和已有的重量种类阶段性计算当前承重时能够放入的重量
当数组中只有2重量的时候，背包承重从2-10都可以放入2的数值
当数组中放入2和3重量的时候，背包承重从5-10
可以放入5，3-4放入3，2只能放入2 当数组中放入2，3，5重量时，背包承重10放入10，8-9放入8，7放入7，5-6放入5…

	 	 2 3 4 5 6 7 8 9 10
 dp数组   0 0 0 0 0 0 0 0  0 
 dp数组   2 2 2 2 2 2 2 2  2   
 dp数组   2 3 3 5 5 5 5 5  5  
 dp数组   2 3 3 5 5 7 8 8 10

最终当每个承重与放入的重量不同时，这个承重就是最小不可求和—4
更详细的解释在代码中：

代码：

#include 
#include 
class Solution {
  public:
    int getFirstUnFormedNum(std::vector<int>& arr, int length) {
        int sum = 0, min = arr[0];
        int i, j;
        for (int i = 0; i < length; i++) {
            sum += arr[i];
            min = arr[i] < min ? arr[i] : min;
        }
        std::vector<int> dp(sum + 1, 0);
        for (i = 0; i < length; i++) { 
        //有length个数据--有length个阶段
		//{2， 3， 5}
		//i=0--2
		//d[10]=2 d[9]=2 d[8]=2 d[7]=2...d[2]=2
		//i=1--3
		//d[10]=5 d[9]=5...d[5]=5 d[4]=3 d[3]=3
		//i=2--5
		//d[10]=10 d[9]=8 d[8]=8 d[7]=7 d[6]=5 d[5]=5
            for (j = sum; j >= arr[i]; j--) 
            {
			//逆序判断背包承重中能够放入的数据
			//当数组中只有2的时候，背包承重从2-10都可以放入2的数值
			//当数组中放入2和3的时候，背包承重从5-10可以放入5，3-4放入3，2只能放入2
			//当数组中放入2，3，5时，背包承重10放入10，8-9放入8，7放入7，5-6放入5...
			
			//核心解释$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
			//dp[j-arr[i]]意思是背包承重为j时，如果已经放置了arr[i]的重量后还能放置的最大重量
			
                if (dp[j] < dp[j - arr[i]] +arr[i])//对每个承重计算当前最大能放置重量
                    dp[j] = dp[j - arr[i]] + arr[i]; //更新背包中能够放入的最大值
                
            }
        }
        
		//最后当承重为n时，放入的重量不为n则认为是最大不可求和
        for (i = min; i <= sum; i++) {
            if (i != dp[i])
                return i;
        }
        return sum + 1;
	}
};

---

有假币

题目链接：

思路：

通过对一堆硬币进行均分称重，判断哪一堆中包含假币（因为假币轻）
平均分三份是最快的方法，两份进行称重（对比出三个的重量 ），每次排除2/3，剩下1/3，比二分法还要快一点。后对最轻的那份再次进行称重，直到称重的个数不足2个时则结束，获得假币；

平均分3份有3种情况，设此时有n枚硬币。

• 最好情况n正好除3，平均分3堆：（1/3）*n，（1/3）*n，（1/3）*n
• 其次当余数是1的时候：（1/3）*n，（1/3）*n，（1/3）*n+1
• 其次当余数是2的时候：是分成（1/3）*n，（1/3）*n+1，（1/3）*n+1，还是（1/3）*n，（1/3）*n，（1/3）*n+2？
  我们来举个栗子说明一下：对于8分成（1/3）*n，（1/3）*n+1，（1/3）*n+1只需要称两次
  
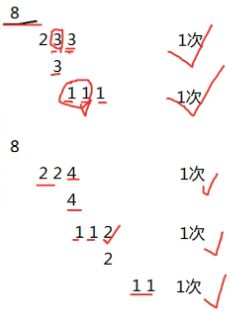
  分成（1/3）*n，（1/3）*n，（1/3）*n+2需要称3次。
  显然分成（1/3）*n，（1/3）*n+1，（1/3）*n+1是更好的。

综上所述：
每次把n除3，有余数就让n加上1即可。
直到n为0或者1的时候就停止。

代码：

#include
using namespace std;
int main() {
    int all;
    while (cin >> all) {
        if (all == 0) 
        {
            break;
        }
        int count = 0;
        
        while (all != 1) 
        {
            all = all/3+(all%3!=0);
            count ++;
        }
        cout << count << endl;
    }

    return 0;
}

---

end