FMCW基本原理 2023年3月20日22:06:57更新
目录
- 1、FMCW概念以及信号模型
- 2、毫米波雷达系统模型
- 3、公式推导
- 4、距离估计
- 5、速度估计
- 6、角度估计
-
- 角度估计原理
- 最大测量角度
- 在同一范围和速度下多个物体的角度估计
- 角度分辨率
- 7、基于3D-FFT雷达处理流程
-
- 处理流程
- 补充
-
- 傅里叶变化频率分辨阈值
- 参考资料
非常感谢博主:调皮连续波(西安电子科技大学 信息与通信工程硕士)
1、FMCW概念以及信号模型
FMCW(Frequency Modulated Continuous Wave),即调频连续波。FMCW技术和脉冲雷达技术是两种在高精度雷达测距中使用的技术。
其基本原理为,发射波为高频连续波,其频率随时间按照三角波规律变化。雷达接收的回波的频率与发射的频率变化规律相同,都是三角波规律,只是有一个时间差,利用这个微小的时间差可计算出目标距离。
2、毫米波雷达系统模型
混频器 mixer:输出瞬时频率等于两个输入正弦曲线的瞬时频率之差。输出相位等于两个输入正弦曲线的相位差,信号模型如下:
输入信号: x 1 = sin [ w 1 t + Φ 1 ) ] x 2 = sin [ w 2 t + Φ 2 ] ] \begin{array}{c}{{x_{1}=\sin[w_{1}t+\Phi_{1})]}}\\ {{x_{2}=\sin[w_{2}t+\Phi_{2}]]}}\end{array} x1=sin[w1t+Φ1)]x2=sin[w2t+Φ2]] 输出信号: x o u t = sin [ ( w 1 − w 2 ) t + ( ϕ 1 − ϕ 2 ) ] x_{o u t}=\sin \left[\left(w_{1}-w_{2}\right) t+\left(\phi_{1}-\phi_{2}\right)\right] xout=sin[(w1−w2)t+(ϕ1−ϕ2)]
3、公式推导
发射信号: x T ( t ) = cos ( 2 π f c t + π S t 2 ) ( 1 ) x_{T}(t)= \cos\left(2\pi f_{c}t+\pi S t^{2}\right)\, \mathrm { (1)} xT(t)=cos(2πfct+πSt2)(1)
S代表信号的斜率,表示信号的频率随着时间的变化率,fc是起始频率。
瞬时频率由公式 θ = ω t = 2 π \theta=\omega t=2 \pi θ=ωt=2π推出,即: f ( t ) = 1 2 π d d t ( 2 π f c t + π S t 2 ) = f c + S t ( 2 ) f(t)={\frac{1}{2\pi}}{\frac{d}{d t}}\left(2\pi f_{c}t+\pi S t^{2}\right)=f_{c}+S t\ (2) f(t)=2π1dtd(2πfct+πSt2)=fc+St (2)
在毫米波雷达系统系统模型中可以看出,雷达接收器将接收信号 x R ( t ) x_{R}(t) xR(t)与发射信号 x T ( t ) x_{T}(t) xT(t)混合,并对所得信号进行低通滤波以产生中频 (IF) 信号 x I F ( t ) x_{IF}(t) xIF(t)。随着 FMCW 信号 x T ( t ) x_{T}(t) xT(t)的频率随时间线性增加, x T ( t ) x_{T}(t) xT(t)和 x R ( t ) x_{R}(t) xR(t)的瞬时频率,即 f T ( t ) f_{T}(t) fT(t) 和 f R ( t ) f_{R}(t) fR(t) 在混合时是不同的。 低通滤波的作用是滤除频率为 f T ( t ) f_{T}(t) fT(t)+ f R ( t ) f_{R}(t) fR(t)的信号分量,同时允许频率为 f T ( t ) f_{T}(t) fT(t)- f R ( t ) f_{R}(t) fR(t)的信号分量通过。 最后可以得到中频信号,表示为公式3。
x I F ( t ) = LPF { x T ( t ) x R ( t ) } = A cos ( 2 π f I F t + ϕ I F ) ( 3 ) x_{\mathrm{IF}}(t)=\operatorname{LPF}\left\{x_{T}(t) x_{R}(t)\right\}=A \cos \left(2 \pi f_{\mathrm{IF}} t+\phi_{\mathrm{IF}}\right)(3) xIF(t)=LPF{xT(t)xR(t)}=Acos(2πfIFt+ϕIF)(3)
正如在 RF 应用中经常使用的那样,正交信号可用于接收机,以降低对中频信号高速采样的要求以及其他设计考虑因素 。 使用正交接收机,接收信号和发射信号的同相和正交信号混合,产生一个复指数中频信号,可以用公式4表示,以供下一步处理。
x I F ( t ) = A e j ( 2 π f I F t + ϕ I F ) ( 4 ) \bm{ x_{\mathrm{IF}}(t)=A e^ {j(2\pi f_{I F}t+\phi_{\mathrm{IF}})} \qquad (4) } xIF(t)=Aej(2πfIFt+ϕIF)(4)
雷达与目标图:

与雷达相距d的物体,在发射信号发出后,到被物体反射回来,经过一段延迟时间到达接收天线,这个过程可以用公式5表示。 τ = 2 d / c ( 5 ) \tau=2d/c \qquad (5) τ=2d/c(5) c为光速
收发信号的时频图

如图所示,当发射和接收的调频信号在时间上重叠时,中频信号频率(即拍频)在有效接收周期内保持恒定,中频频率可以由公式6表示。
f I F = f T ( t ) − f R ( t ) = S τ ( 6 ) f_{\mathrm{IF}}=f_{T}(t)-f_{R}(t)=S\tau\ \qquad (6) fIF=fT(t)−fR(t)=Sτ (6) 其中S是调制信号的斜率,S=B/Tc τ为收发信号的时间差。
对于复指数形式的中频信号公式: x I F ( t ) = A e j ( 2 π f I F t + ϕ I F ) ( 4 ) \bm{ x_{\mathrm{IF}}(t)=A e^ {j(2\pi f_{I F}t+\phi_{\mathrm{IF}})} \qquad (4) } xIF(t)=Aej(2πfIFt+ϕIF)(4)
由于调制信号的起始频率远大于,所以 ϕ I F = 2 π f c τ + π S τ 2 ≈ 2 π f c τ \phi_{\mathrm{IF}}\,=\,2\pi f_{c}\tau+\pi S\tau^{2}\approx2\pi f_{c}\tau ϕIF=2πfcτ+πSτ2≈2πfcτ,由此可得到中频信号的频率和相位表达式。
f I F = S τ = 2 S r / c ( 9 ) ϕ I F = 2 π f c τ = 4 π r / λ ( 10 ) \begin{array}{l c l}{{f_{\mathrm{IF}}=S\tau=2S r/c\ \qquad \quad \quad(9)}}\\ {{\phi_{\mathrm{IF}}=2\pi f_{c}\tau=4\pi r/\lambda\ \mathrm{ \ \qquad(10)}}}\end{array} fIF=Sτ=2Sr/c (9)ϕIF=2πfcτ=4πr/λ (10)
4、距离估计
- 探测距离
如公式9所示,中频信号与距离的关系可得: r = f I F ∗ c / 2 S r=f_{IF}*c/2S r=fIF∗c/2S
频域解决办法:
由于中频信号的频率固定,所以在对中频信号进行傅里叶变换,得到频谱,在单个目标的情况下,会在频域产生一个单峰。
这个峰值的横坐标就是对应时域的中频信号频率,由此可以根据公式计算距离r。
如果存在多个目标且距离不一的时候,得到的中频信号和频谱图如下:
如果距离过于接近,那么就会存在频谱峰值重叠的现象,这个时候可以用距离分辨率来衡量。
- 距离分辨率
距离分辨率:范围分辨率是指分辨两个间隔很近的对象的能力。如下图,由于距离过于接近,导致频谱只有一个峰值,无法区分目标。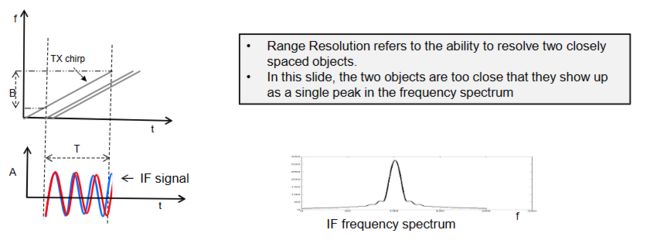
这两个对象可以通过增加中频信号的长度来解决,这也会按比例增加带宽。因此直观地说:带宽越大=>分辨率越好。
公式推导:
由于Tc时间内可以分辨时间间隔超过1/Tc Hz的频率分量,所以可以进行如下推导。
Δ f > 1 T c ⇒ S 2 Δ d c > 1 T c ⇒ c B T c ⇒ c B ( s i n c e B = S T c ) \Delta f>{\frac{1}{\mathrm{T_{c}}}}\Rightarrow{\frac{S2\Delta\mathrm{d}}{\mathrm{c}}}>{\frac{1}{\mathrm{T_{c}}}}\Rightarrow{\frac{\mathrm{c}}{\mathrm{BT_{c}}}}\Rightarrow{\frac{\mathrm{c}}{\mathrm{B}}}\quad{\mathrm{(since~B=ST_{c})}} Δf>Tc1⇒cS2Δd>Tc1⇒BTcc⇒Bc(since B=STc) 结合距离公式 r = f I F ∗ c / 2 S r=f_{IF}*c/2S r=fIF∗c/2S可以得到距离分辨率公式为: d r e s = c 2 B d_{r e s}={\frac{c}{2B}} dres=2Bc。
因此,范围分辨率(dres)仅取决于chirp扫描的带宽(B)。
- 最远探测距离
由于中频信号一般需要通过低通滤波器和ADC模数转化器,然后在DSP中进行数字信号处理,因此此处涉及到采样率的问题,中频带宽因此受到ADC采样率(Fs)的限制 F S ≥ S 2 d m a x c \mathrm{F}_{\mathrm{S}}\geq{\frac{\mathrm{S2dmax}}{\mathrm{c}}} FS≥cS2dmax (不等式右边等于最大中频信号频率)
由此可以得到最远探测距离公式: d m a x = F s c 2 S \mathrm{d}_{\mathrm{max}}={\frac{\mathrm{F}_{s}c}{2S}} dmax=2SFsc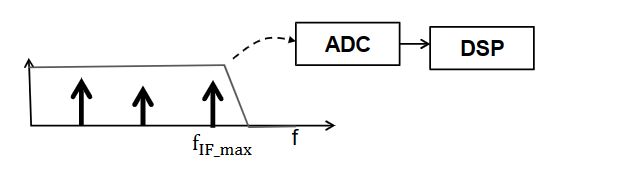
5、速度估计
为了测量速度, FMCW 雷达会发射两个间隔 Tc 的chirp。每个反射的chirp通过 FFT加以处理,以便检测物体的距离(距离 FFT)。对应于每个线性调频脉冲的距离 FFT 将在同一位置出现峰值,但相位不同。该测得的相位差对应于速度为 vTc 的物体的移动 。
如图所示,不同相位的中频信号在频谱的区别,峰值的相位等于正弦曲线的初始相位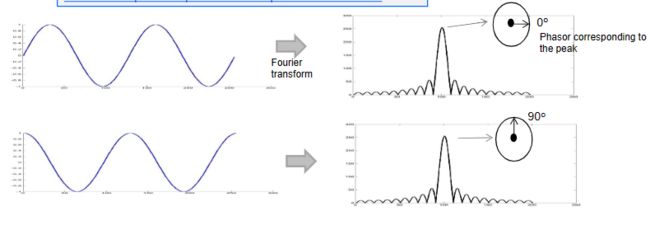
推导过程:
回波是发送波的一段时间延时,测量物体距离变化的中频IF的C, F相位差即为A, D相位差(B与E都是TX延时版本)
Δ ϕ ≡ ϕ D − ϕ A = 2 π f c Δ τ = 4 π Δ d λ \Delta\phi\equiv\phi_{D}-\phi_{A}=2\pi f_{c}\Delta\tau={\frac{4\pi\Delta d}{\lambda}} Δϕ≡ϕD−ϕA=2πfcΔτ=λ4πΔd, d为目标距离,d=v*Tc
因此可以得到 ω = 4 π v T C λ ⇒ v = λ ω 4 π T c \bm{\omega=\frac{4 \pi v T_{C}}{\lambda} \Rightarrow v=\frac{\lambda \omega}{4 \pi T_{c}}} ω=λ4πvTC⇒v=4πTcλω
考虑一下斜率为S=50MHz/us的chirp信号,如果雷达前方的物体位置改变1mm(对于77GHz雷达,1mm=λ/4),则相位变化为: Δ ϕ = 4 π Δ d λ = π = 18 0 ∘ \Delta\phi={\frac{4\pi\Delta d}{\lambda}}=\pi=180^{\circ} Δϕ=λ4πΔd=π=180∘,中频信号的频率变化为 Δ f = S 2 Δ d c = 333 H z \Delta\mathbf{f}={\frac{S2\Delta d}{c}}=333\mathrm{{Hz}} Δf=cS2Δd=333Hz,虽然中频信号的频率变化了333Hz,但是相对于整个观察窗口来说占比非常小,所占循环大小为 Δ f T c = 333 × 40 × 1 0 − 6 = 0.013 \Delta f T_{c}=333 \times 40 \times 10^{-6}=0.013 ΔfTc=333×40×10−6=0.013。这种变化在频谱中是无法辨别的
- 同一距离处多物体速度测量
当相同距离有多个移动物体时,range-FFT后会在同一位置产生峰值,该峰值由距离相同目标合并而来,因为区分不开,之前单个目标通过连续发送两个chirp比较峰值相位的方法将不起作用**,**这种情况下可通过发送一组N个等间隔chirp信号,这一组也成为一帧,如下图所示,测量相同距离有两个不同速度的物体。
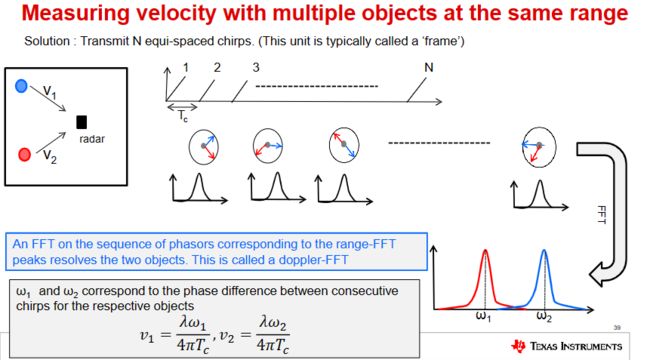
做完range-FFT后,如下图所示,在N行同位置产生峰值,每个峰值相位包含两个物体的相位即下图中红色与蓝色向量合成(根据欧拉公式可理解成多个三角函数的累加),对这些range-FFT峰值做FFT即多普勒Doppler-FFT,如下图14所示,因为是等间隔Tc, Δ ϕ \Delta\phi Δϕt表示的是range-FFT后的wt,所以做完Doppler-FFT得出的w1, w2相等间隔内表示是 Δ ϕ \Delta\phi Δϕ即两个物体对应的线性调频的相位差。
每个range轴上的单位表示一个距离门,在一个距离门的基础上,对每一列做FFT即为Doppler FFT。
- range-fft:对每个chirp进行fft运算,可以得到一个(多个)目标的峰值,这个峰值在频谱中能否进行区分取决于恩变量能否满足。(横坐标长度就是采样点数,每个点称为距离门,然后乘上相应的距离分辨率(或者是转化比例)就可以得到实际的距离)
- doppler-fft:对每一个距离门上面的range-fft峰值进行fft,也称为Doppler-FFT(距离FFT对应的相量序列的FFT,产生的峰值可以得到多个目标。这就是的多普勒-FFT
- )
- 最终得到的图是range-velocity的平面图,如上图所示,图中第一行最下面的点表示速度为0的点,并且距离在第八个距离门处。
需要考虑和解决的问题:“多普勒FFT”的速度分辨率(vres)是多少即v1和v2之间的最小间隔是多少,使它们在多普勒FFT中显示为两个峰值?
====》在傅里叶变换中,长度为N的序列上的FFT可以分离两个频率ω1和ω2,只要|ω1–ω2|>2π/N。
6、角度估计
角度估计原理
当目标距离发生很小变化时会引起相位变化,因此可根据物体与不同天线之间的距离差Δd导致的不同相位差来计算到达角AOA(Angle of Arrival)
TX天线传输一帧chirp。对应于每个RX天线的2D-FFT将有峰值。在相同的位置,但不同的阶段。测量的相位差(ω)可用于估计物体的到达角。

公式推导:
Δ d = d ∗ sin θ \Delta \mathrm{d}=\mathrm{d}^{*} \sin \theta Δd=d∗sinθ , ω = 2 π Δ d λ \omega={\frac{2\pi\Delta\mathrm{d}}{\lambda}} ω=λ2πΔd
ω = 2 π d s i n θ λ ⇒ θ = sin − 1 ( λ ω 2 π d ) \omega={\frac{2\pi\mathrm{d}sin{\theta}}{\lambda}}\Rightarrow\theta=\sin^{-1}{\left({\frac{\lambda\omega}{2\pi d}}\right)} ω=λ2πdsinθ⇒θ=sin−1(2πdλω)
由公式可知,θ和w不是线性的,根据正弦函数的波形可知,sinθ在0度处斜率大变化快,90度处斜率为0变化最慢,因此当θ为0度时估算最精确,90度时估算准确度下降。
最大测量角度

当Δϕ>0,目标在雷达左侧,当Δϕ<0,目标在雷达右侧,如果不指定最大测量范围,如上图所示,会分不清在雷达左侧还是右侧。根据上文可知,不模糊速度测量的相位差要求小于180°,即: |ω| < 180°。所以进行如下推导:
2 π d s i n ( θ ) λ < π ⇒ θ < s i n − 1 ( λ 2 d ) {\frac{2\pi\mathrm{d}\mathrm{sin}(\theta)}{\lambda}}<\pi\Rightarrow\ \theta<\mathrm{sin}^{-1}\left({\frac{\lambda}{2\mathrm{d}}}\right) λ2πdsin(θ)<π⇒ θ<sin−1(2dλ),因此最大测量角度为: θ m a x = sin − 1 ( λ 2 d ) {\mathfrak{\theta}}_{\mathrm{max}}={\sin}^{-1}\left({\frac{\lambda}{2\mathrm{d}}}\right) θmax=sin−1(2dλ),这个也是间隔为d的两个天线可以服务的最大视场。间距d为λ/2时,视场最大为±90°。天线间距决定着最大测量角
在同一范围和速度下多个物体的角度估计
两个物体与雷达等距,速度相同时,通过N个接收天线测量到达角,对回波做angle-FFT进行相位解析,w1, w2为各物体对应连续线性调频信号的相位差
angle-fft:对对应于2D-FFT峰值的相量序列进行FFT,解析这两个对象,这称为角度FFT。这个FTT是从接收天线的维度展开的。

各目标角度: θ 1 = sin − 1 ( λ ω 1 2 π d ) , θ 2 = sin − 1 ( λ ω 2 2 π d ) \theta_{1}=\sin^{-1}\left({\frac{\lambda\omega_{1}}{2\pi d}}\right)\;\;\;,\,\theta_{2}=\sin^{-1}\left({\frac{\lambda\omega_{2}}{2\pi d}}\right) θ1=sin−1(2πdλω1),θ2=sin−1(2πdλω2)
角度分辨率
角度分辨率(θRes)是两个对象在角度-FFT中显示为单独峰值的最小角度间隔。如下图所示,随着到达角AOA的增加,角度分辨率下降。

公式推导:
假设θ变了引起的频率变化用公式表示为:
ω = 2 π d s i n θ λ \omega={\frac{2\pi\mathrm{d}sin{\theta}}{\lambda}} ω=λ2πdsinθ ===》 Δ ω = 2 π d λ ( sin ( θ + Δ θ ) − sin ( θ ) ) \Delta{\omega}=\frac{2\pi\bf{d}}{\lambda}\bigl(\sin(\theta+\Delta\theta)-\sin(\theta)\bigr)_{\mathrm{{\scriptsize}}} Δω=λ2πd(sin(θ+Δθ)−sin(θ))
根据导数关系: sin ( θ + Δ θ ) − sin ( θ ) Δ θ = cos ( θ ) \frac{\sin (\theta+\Delta \theta)-\sin (\theta)}{\Delta \theta}=\cos (\theta) Δθsin(θ+Δθ)−sin(θ)=cos(θ),上式可以化为: Δ ω = 2 π d λ ( sin ( θ + Δ θ ) − sin ( θ ) ) ≈ 2 π d λ cos ( θ ) Δ θ \Delta\omega=\frac{2\pi d}{\lambda}\,(\sin(\theta+\Delta\theta)-\sin(\theta))\,\approx\frac{2\pi d}{\lambda}\cos(\theta)\Delta\theta Δω=λ2πd(sin(θ+Δθ)−sin(θ))≈λ2πdcos(θ)Δθ
根据傅里叶变换理论,在傅里叶变换中,长度为N的序列上的FFT可以分离两个频率ω1和ω2,只要|ω1–ω2|>2π/N。进一步推导公式得:
Δ ω > 2 π N \Delta{\omega}>{\frac{2\pi}{N}} Δω>N2π => 2 π d λ c o s ( θ ) Δ θ > 2 π N \frac{2\pi\mathrm{d}}{\lambda}\mathrm{cos}(\theta)\,\Delta\theta>\frac{2\pi}{\mathrm{N}} λ2πdcos(θ)Δθ>N2π=> Δ θ > λ N d c o s ( θ ) \Delta\theta>\frac{\lambda}{\mathrm{Ndcos}(\theta)} Δθ>Ndcos(θ)λ
角度分辨率为: Δ θ > λ N d c o s ( θ ) \Delta\theta>\frac{\lambda}{\mathrm{Ndcos}(\theta)} Δθ>Ndcos(θ)λ,通常情况下d=λ/2以及 θ=0,得角度分辨率为: θ r e s = 2 N \theta_{r e s}=\frac{2}{N} θres=N2。
由公式知天线个数以及天线间间距有关决定着角度分辨率,天线间间距决定着角度估计值。
角度估计和速度估计都是依据相同的数学模型,如下图所示,通过N个离散的信号相位变化,分别在空间域、时间域进行估计。角分辨率依赖于天线阵列的长度Nd,速度分辨率依赖于帧周期长度;最大视场角依赖于天线间距,最大无模糊测速依赖于chirp的时间长度
7、基于3D-FFT雷达处理流程
处理流程

:::info
快时间和慢时间维度:在毫米波雷达数据处理中,通常会将雷达接收到的信号进行时域处理,得到快时间(range dimension)和慢时间(azimuth dimension)两个维度。
- 快时间维度(range dimension)通常是指雷达发射的信号在空间中传播和反射后返回接收器所需的时间,也称为“往返时间”。在快时间维度上,雷达接收到的信号是以一定时间间隔(即脉冲宽度)的形式进行采样的,每个采样点对应着一个距离。通过对快时间维度的信号进行处理,可以提取出目标与雷达之间的距离信息。
- 慢时间维度(azimuth dimension)通常是指雷达的扫描过程所需要的时间。在慢时间维度上,雷达可以通过机械扫描、电子扫描或者二者的组合进行目标探测。通过对慢时间维度的信号进行处理,可以提取出目标在水平方向上的位置信息。
总之,快时间维度和慢时间维度是毫米波雷达中两个重要的时域维度,它们共同组成了雷达接收到的三维数据。对这两个维度进行处理,可以提取出目标的距离和位置信息,实现目标探测和跟踪。
:
补充
傅里叶变化频率分辨阈值
参考资料
雷达信号处理之3D-FFT原理(附带MATLAB仿真程序)
[解疑][TI]TI毫米波雷达系列(三):调频连续波雷达回波信号3DFFT处理原理(测距、测速、测角)
FMCW毫米波雷达基础原理学习一
汽车FMCW毫米波雷达信号处理流程
mmwaveSensing-FMCW-offlineviewing_0.pdf
(TDM-MIMO FMCW雷达入门教程)Signal_Processing_for_TDM_MIMO_FMCW_Millimeter-Wave_Radar_Sensors.pdf
毫米波雷达传感器基本原理(英文版).pdf
毫米波雷达传感器基本原理(中文版).pdf