2014，EuroGP，Semantic crossover based on the partial derivative error

---

Abstract

语义遗传算子的发展对于提高遗传编程的性能有着极大的兴趣。语义遗传算子传统上是通过实验或基于理论的方法开发的。我们目前的工作提出了一种在两种传统方法中发展起来的新的语义交叉。我们提出的语义交叉算子是基于使用通过树传播的误差的导数。这个过程决定了第二个父代的交叉点。结果表明，我们的方法提高了遗传规划在理性符号回归问题上的性能。

1 Introduction

为了提高遗传规划的性能，人们提出了语义遗传算子。语义算子利用表型的信息来创建新的个体。发展语义算子有两种途径，第一种是基于实验的，第二种是基于理论的。

基于实验的方法产生基于适应度函数或树的行为的语义交叉。布利克勒等[ 1 ]提出只选择那些在适应度函数中有影响的节点作为交叉点，这是用节点上的一个标志来实现的，即在评估树时设置。Nguyen等人的[ 2、3]产生的后代在语义上不同于其父母；这种差异是通过评估一组随机输入中的个体来衡量的。

另一方面，遵循基于理论的方法，Beadle等人[4、5]提出了一个语义算子，该算子只接受子代，如果它在语义上与父代不等价。非等价性通过使用简化的有序二叉决策图进行验证，该决策图也被用于开发语义不同的初始种群(参见[6] )。此外，Krawiec等人[ 7 ]发展了一个几何语义交叉的近似，这是非常重要的，因为具有将景观转化为圆锥体的潜力，此外，Moraglio等[8]已经证明了创建几何语义交叉和变异的可行性。Moraglio等人提出的生成子代的过程干净且易于实现；然而，它的缺点是所构造的子代总是大于其父代的长度之和，这给它的应用带来了限制。尽管如此，万内斯基等[9]克服了这一原始限制，允许使用GP中使用的传统参数执行算法。我们目前的贡献提出了一种基于树的遗传编程(GP)的语义交叉，介于基于实验和基于理论的方法之间。提出的语义交叉是基于误差的导数，即适应度函数$f(p)$的导数。在符号回归问题中，通常计算适应度函数为：$f(p)={\sum }_{(x,y)\in \mathcal{T}}(y-p(x){)}^2$，其中 $\mathcal{T}=\{(x_i,y_i)：i=\mathrm{1..}N\}$为训练集，$p(x)$表示个体$p$在输入$x$上的输出。

这里提出的语义交叉是通过：

1. 计算$\frac{\partial f}{\partial v}$等价于反向传播算法[10]更新人工神经网络的权重¹。然而，在我们的过程中，v是从第一个父节点中随机选择的节点，而在反向传播中v总是一个常数，即权重。
2. $\frac{\partial f}{\partial v}$的结果用于选择第二父代的交叉点。
3. 这两个点用于执行传统的子树交叉。

• ¹在GP中使用反向传播已经在文献[11-14 ]中提出。

结果表明，在所使用的1100个有理函数上，用所提出的语义交叉增强的GP在统计上优于传统交叉的GP
本论文的结构安排如下。第2节展示了我们新颖的语义交叉。第三节描述了用于生成符号回归问题的过程和用于说明我们方法有效性的GP系统。第四部分，结论和未来方向。

2 Semantic Crossover Based on Partial Derivative Error

提出的语义交叉计算如下：a ) 设$v$是从第一个父节点中随机选择的节点；b )给定$v$，计算$\frac{\partial f}{\partial v}$；C ) 利用关于$v$的偏导数的信息从第二个父节点中选择一个节点$u$；d ) 最后，以$v$和$u$为交叉点进行子树交叉。本节其余部分对这一过程进行了详细描述。2.1节给出了计算$\frac{\partial f}{\partial v}$的过程，即在树结构中实现的反向传播算法；和2.2节介绍了$u$的选取过程。

2.1 Backpropagation

第一步，为了描述提出的语义交叉，展示计算$\frac{\partial f}{\partial v}$的过程。如前所述，利用反向传播算法可以得到$\frac{\partial f}{\partial v}$。反向传播可以很容易地用[10]中的思想来解释。R. Rojas用一种图形化的表示法对其进行了解释，这种表示法可以很容易地在基于树的GP中进行编码。

让我们通过计算链规则来描述反向传播，即$\frac{\partial g(h(x))}{\partial x}$。第一步，计算$g(h(x))$，见图 1 的上半部分，注意每个内部节点被分成两部分；右边部分对应节点的输出，左边部分存储每个节点所示操作的输出。信息的流动由箭头指示。第二步，也是最后一步，向后遍历树，见图 1 的下半部分。这个向后的步骤是通过向根节点提供一个常数来完成的，在这种情况下是1，然后将这个常数乘以每个节点左侧存储的值。这个过程递归地持续，直到到达一片叶子。在图的下半部分观察到，在这个过程的最后得到了$\frac{\partial g(h(x))}{\partial x}$。

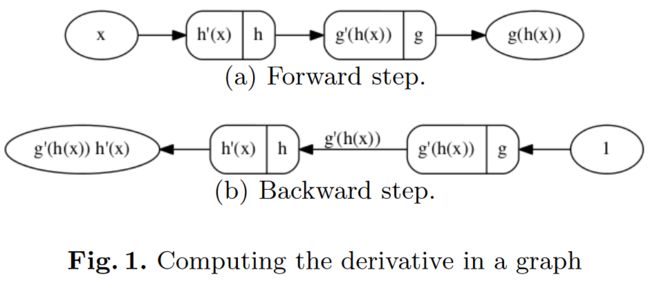
• 图 1 . 计算图中的导数

继续反向传播的描述，假设叶子结点是一个常数$w$，那么上述过程计算$\frac{\partial f}{\partial w}$。这可以用来按照规则$w=w-\nu \frac{\partial f}{\partial w}$更新$w$，其中$\nu$是学习因子。这种更新可以针对每个训练案例进行，也可以针对整个训练集进行，前者称为增量学习，后者称为批学习。在批量学习中，使用规则$w=w-\nu {\sum }_{i=1}^{|\mathcal{T}|}\frac{\partial f_i}{\partial w}$更新$w$，其中$f_i$为训练集第$i$种情况下的误差。除此之外，弹性反向传播(RPROP) [15]可以只使用符号和不同的$\nu$来实现增加和减少的值，即$w=w-{\nu }_x\cdot sign({\sum }_{i=1}^{|\mathcal{T}|}\frac{\partial f_i}{\partial w})$，其中$x$代表减少或增加的学习率。

为了完整地展示这一过程，图 2 给出了一个例子。在图(a)的左边，说明了一个用树表示的函数。在右边(b)中，我们有相同的树被提出，并提供了计算导数所需的额外信息。注意对于有两个参数的函数需要两个槽。例如，在product中，由于$\frac{\partial x\cdot y}{\partial x}=y$，且第二部分包含第一输入，因此第一部分存储第二输入。我们已经说明了sum节点存储ones 是关于每个输入的偏导数。但是，不需要在求和节点上存储信息，仅为保证实例的清晰描述而被包含。

• 图 2. 树有一个额外的存储来计算导数

图 3 给出了一个完整的例子，在左边(a)中，所有的常数都有取值，例如$a=0.2，b=-1.2$和$c=0.3$，并且有两个输入$x_1=-0.5$和$x_2=0.5$。此外，所求函数为$y(x)=0.5x^2-2.25x+0.6$，得到训练集$\mathcal{F}=\{(-0.5,1.85)，(0.5、-0.4)\}$。此时树的输出为$(0.95,-0.25)$。在评估过程中，即前向步骤中，所有的偏导数都被计算并存储在各自的节点中；这在每个节点(图的左边)的下半部分显示。后退步需要给节点输入一个值，这个值是误差的导数，它取决于用来计算误差的函数。令$f(p)=(y-p{)}^2$为误差函数，则其关于$p$的导数为$-2(y-p)$。设$y=(1.85,-0.4)$为期望输出，$p=(0.95,-0.25)$为树的输出，则误差的导数值为$-2(y-p)=(-1.8,0.3)$。这个值通过树传播，直到达到一个常数。最后，使用到达该特定节点的所有值的符号更新此常数。常数根据符号是正还是负分别减小或增大。如果某个常量接收到的值为零，则该常量不更新。

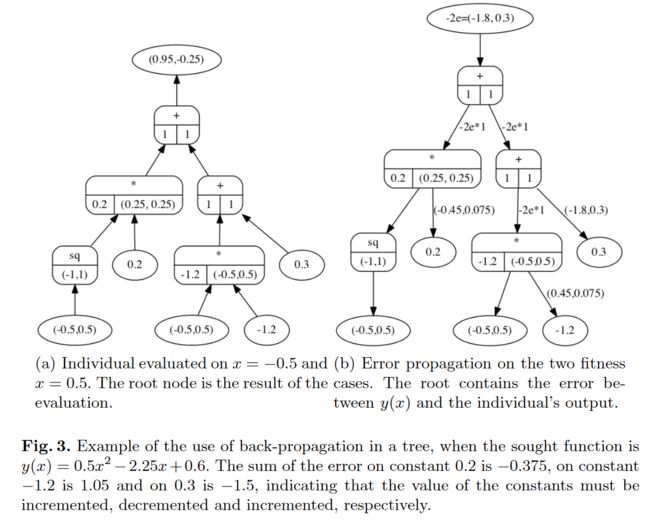
• 图 3. 当求函数为$y(x)=0.5x^2-2.25x+0.6$时，在树上使用反向传播的例子。常数$0.2$上的误差之和为$-0.375$，常数$-1.2$上的误差之和为$1.05$，常数$0.3$上的误差之和为$-1.5$，表明常数的取值必须分别递增、递减和递增。

2.2 Selecting the Crossing Points

到目前为止，我们已经描述了在树上实现的反向传播算法。该算法是递归的，在反向传播步骤中，当到达一片叶子时停止；然而，任何事情都不能阻止它在某个特定的节点。假设程序在节点$v$处停止($v$是从第一个父代中随机选取的)，然后，在这一点上，得到$\frac{\partial f}{\partial v}$，这表明$v$返回的值是减少还是增加取决于$\frac{\partial f}{\partial v}>0$还是$\frac{\partial f}{\partial v}<0$。

为了选择第二个父代的交叉点，执行以下步骤。令$e$为$\text{sign}(\frac{\partial f}{\partial v})$，$e_i$对应第$i$个训练样本中偏导数误差的符号，$v$对应第1个父代的交叉点。在基于树的GP中，$v$可以看作是一棵完整的树，即可以从父代中移除$v$，并将其作为新个体。在此背景下，令$p^v$表示$v$在$\mathcal{T}$输入下的输出，$p_i^v$表示$v$在第$i$个训练样本下的输出。等价地，对于第二个父节点，我们可以计算所有节点的输出，令$s^j$表示第二个父代中节点$j$的输出。利用$e，p$和$s$，我们可以找到第二父代的交叉点$u$，as：

为了证明方程(1)，我们分析了在方程(1)的最大值处发现的两种可能的情形。首先，当$e_i>0$时，$s_i^u$大于$p_i^v$，$p_i^n-s_i^m$为正。另一方面，$e_i<0$意味着$p_i^n-s_i^m$为负；但是，$e_i<0$也是负的，结果是正的。在这种情况下，${\sum }_{i}sign(p_i^v-s_i^u)\cdot e_i$等于$|\mathcal{T}|$，因为$p_i^v-s_i^u$和$e_i$具有等价的符号。

4 Conclusions

我们的工作提出了一种新的基于误差导数的语义交叉算子的开发。结果表明，根据方程 1 选择第二个父代的交叉点可以显著提高GP系统的学习能力。GPPDE在几乎所有测试的(1100中有1095优越)问题中都表现出了最好的性能，并且与本文提出的系统相比，以及与本课题组之前提出的20个系统相比，它也获得了平均最好的性能[18]。

提出的改进需要在树上进行大量的计算。也就是说，对于种群中每棵树的每个节点，都需要保留输出，以及输出的导数。这可能是一个缺点，因为该技术可能仅限于小种群和/或小树。然而，这种信息量所能提供的全部潜力尚未得到适当的发掘。例如，为了评估一个子代，只需要重新计算值发生改变的节点，这将使算法更快。另一方面，可以衡量每个节点的适应度，并根据适应度动态地做出决策。提出的语义交叉算子的另一个局限性是函数集中的所有函数都需要可导。这可能是一些问题的一大弊端；然而，对于符号回归问题，仅仅使用可导函数似乎是合理的。

补充

其中涉及求偏导数，对谁求偏导谁就是自变量，其余都是常量，如 $y=a{x}^2$ 对 a 求偏导，那么 $x^2$ 整体就是常数，此时偏导数为 $x^2$

References

Graff M, Graff-Guerrero A, Cerda-Jacobo J. Semantic crossover based on the partial derivative error[C]//Genetic Programming: 17th European Conference, EuroGP 2014, Granada, Spain, April 23-25, 2014, Revised Selected Papers 17. Springer Berlin Heidelberg, 2014: 37-47.

算法原理

如图 2 所示，从叶节点开始对每一个函数节点所构成的整颗子树以此函数节点为根节点，分别对左右子树求偏导从左到右从下到上的顺序 $sq(x)$ 对 $x$ 的偏导为 $2x$, $a{x}^2(asq(x))$ 对左子树 $sq(x)$ 的偏导为 $a$, 对右子树 $a$ 的偏导为 $sq(x)$, $bx$ 对左子树 $x$ 的偏导为 $b$， 对右子树 $b$ 的偏导为 $x$, $bx+c$, 对左子树 $bx$ 的偏导为 1， 对右子树 $c$ 的偏导为 $1$, $a{x}^2+bx+c$ 对左子树 $a{x}^2$ 的偏导为 1， 对右子树 $bx+c$ 的偏导数维 1。

示例：

图 3 (a)：$a=0.2，b=-1.2$和$c=0.3$，两个数据样本$X=\{-0.5,0.5\}$, 整棵树的输出为$\{-0.5,0.95\},\{0.5,0.25\}$, 如(a) 中根节点所示，其余节点，根据图 2 中计算偏导数的方式，从叶子节点开始计算左右子树的偏导数，并将样本值$X=\{-0.5,0.5\}$ 带入变量$x$，得到每个节点的左右子树偏导数值。

假设：适应度函数为：$f(p)=(y-p{)}^2$，则其关于$p$的导数为$-2(y-p)$。最终树的目标为：$y(x)=0.5x^2-2.25x+0.6$，则此时$y=(1.85,-0.4)$为期望输出，$p=(0.95,-0.25)$为树的输出，则误差的导数值为$-2(y-p)=(-1.8,0.3)$。这个值通过树传播，直到达到一个常数。最后，使用到达该特定节点的所有值的符号更新此常数。常数根据符号是正还是负分别减小或增大。如果某个常量接收到的值为零，则该常量不更新，如图3中(b)所示，-2e, 其中 e 表示导数误差，这里为$(y-p)$, -2e 整体为适应度函数的导数$-2(y-p)$

根据求得的偏导数选择交叉点：

假设程序在节点$v$处停止(反向传播后停止的节点存在多处，$v$是从第一个父代中随机选取的)，然后，在这一点上，得到$\frac{\partial f}{\partial v}$，这表明在从根节点，传递误差方向的过程中,$v$返回的值是减少还是增加取决于$\frac{\partial f}{\partial v}>0$还是$\frac{\partial f}{\partial v}<0$。

为了选择第二个父代的交叉点，执行以下步骤。令$e$为$\text{sign}(\frac{\partial f}{\partial v})$，即$e_i$对应第$i$个训练样本中偏导数误差的符号，$v$对应第1个父代的交叉点。在基于树的GP中，$v$可以看作是一棵完整的树，即可以从父代中移除$v$，并将其作为新个体。在此背景下，令$p^v$表示$v$在$\mathcal{T}$输入下的输出，$p_i^v$表示$v$在第$i$个训练样本下的输出。等价地，对于第二个父节点，我们可以计算所有节点的输出，令$s^j$表示第二个父代中节点$j$的输出。利用$e，p$和$s$，我们可以找到第二父代的交叉点$u$，as：

为了证明方程(1)，我们分析了在方程(1)的最大值处发现的两种可能的情形。首先，当$e_i>0$时，$s_i^u$大于$p_i^v$，$p_i^n-s_i^m$为正。另一方面，$e_i<0$意味着$p_i^n-s_i^m$为负；但是，$e_i<0$也是负的，结果是正的。在这种情况下，${\sum }_{i}sign(p_i^v-s_i^u)\cdot e_i$等于$|\mathcal{T}|$，因为$p_i^v-s_i^u$和$e_i$具有等价的符号。

即通过在第一个父代中选择一个随机交叉点 $v$，在第二个父代中遍历所有点，选择出节点$j$, 使得在每个样本下的 $p_i^v-s_i^j$ 的符号乘以对应的偏导数的和最大。这样来保证，交叉的点拥有朝着减少误差的方向产生子代

算法缺点

对树中每个节点都要计算偏导数，并存储下来，仅适用于小型树结构，并且需要涉及到的所有函数都可导。