数据结构---八大排序

专栏：算法
个人主页：HaiFan.
本章内容为大家带来排序的相关内容，希望大家能多多支持。

前言

排序在日常生活十分的重要，买一个东西的时候，肯定要看价格；打游戏的时候的段位排名；游戏下载次数的排行等等，都需要用到排序，下面，HaiFan来为大家介绍一下常用的排序方法。

插入排序：直接插入排序和希尔排序

选择排序：选择排序：堆排序

交换排序：冒泡和快排

归并排序：归并

计数排序

插入排序

直接插入排序是一种最简单的排序方法，将一条记录插入到已排好的有序表中，从而完成排序。

直接插入排序

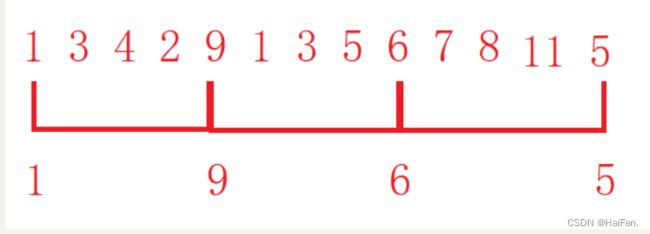
在这里以升序为例

1. 每次都先将一个待排序的元素(tmp)给记录下来
2. 依次与tmp之前的元素进行比较
3. 如果a[i] > tmp，则让a[i]向后移动;若a[i] < tmp，说明找到了合适的位置，直接让tmp插入这个位置即可
4. 重复1，2，3的操作，直到元素排序完成

---

下面是代码实现

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];//要排序的元素

		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

值得注意的是，for循环里的n - 1，如果换成n就会造成越界访问。

希尔排序(缩小增量排序)

希尔排序是在直接插入排序的基础上做了改进，使得排序效率更高。

希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

来源—百科

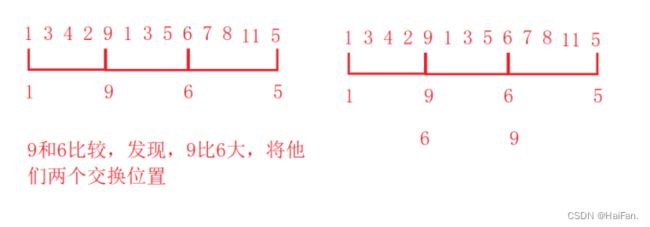
1.我觉得这个排序方法更像分组排序，先把一个序列分成n个小组，

2.小组的第一个依次排序，每组的第二个依次排序…，排完之后，该序列会变成一个接近有序的序列

3.然后继续分组，把组进行细分，然后执行2的步骤，直到变成一个元素一组。此时序列就会变得有序

当gap大于1的时候，都是预排序，让序列接近有序，当gap==1的时候，因为序列已经接近有序，这个时候排序就会非常的块，

---

代码如下

void ShellSort(int* a, int n)
{
	int gap = n;//表示分成几组

	while (gap > 1)
	{
		gap /= 2;//每次分组都/2

		for (int i = 0; i < n - gap; i += gap)
		{
			int end = i;
			int tmp = end + gap;//直接插入排序的tmp是end的下一个元素，tmp和tmp之前的元素进行比较；而希尔排序的tmp是下一组的第一个元素，end是本组的第一个元素，组与组之间进行交换
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

选择排序

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

来源–百科

这个排序挺直观的，两层for循环即可搞定。

以升序为例

1.第一层循环(变量i表示循环中的变量)用来表示需要交换的位置，我们要升序排列，第一个元素肯定要是最小的，而第一层for循环控制的就是位置，将最小的元素放入第一个位置里

2.第二层循环用来遍历序列，当然是从i＋1开始遍历的，因为本身不需要遍历，遇到比a[i]小的，就交换

3.重复的执行1和2，直到遍历完

---

代码如下

void SelectSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		for (int j = i + 1; j < n; j++)
		{
			if (a[i] < a[j])
			{
				swap(a[i], a[j]);
			}
		}
	}
}

堆排序

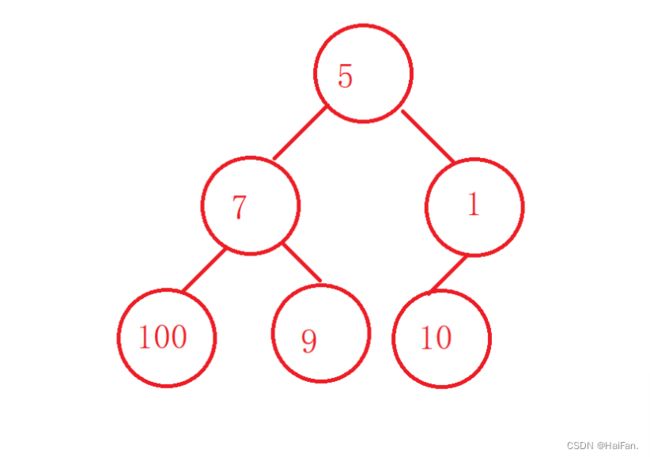
堆排序嘛，肯定要先建立一个堆，这里我们可以选择向上或者向下建堆的方式，本文是以向下建堆为例。建堆是有要求的，左右子树都要是大根堆或者小根堆，这样在建堆的过程中，才不会乱。

在向下建堆的时候，我们要从哪一棵子树开始呢？

建堆的目的是使每棵子树都是大根堆或者小根堆的状态，所以我们要找一个能把所有子树都包含的位置，也就是下标为3的位置(根的下标为0，4的下标为2)，这样就能完成建堆。

以这个图为例，讲解一下建堆(大根堆)的过程。

1.找到最后一个非叶子节点：因为堆的定义是一棵完全二叉树，因此最后一个节点的父节点就是最后一个非叶子节点。

2.从最后一个非叶子节点开始，逐个向下调整节点，使得以该节点为根节点的树满足堆的性质，当然建堆的时候，需要注意跟左右孩子进行比较，选出最大的那个孩子和父节点进行比较。

3.重复2操作，直至堆中所有节点都满足堆的性质，此时堆就构建完成了。

4.堆排序就是将堆顶元素与堆的最后一个元素进行交换，然后向下调整堆，并且总元素个数减1.

---

代码如下；

void JustDown(int* a, int parent, int s)
{
	int child = parent * 2 + 1;

	while (child < s)
	{
		if (child + 1 < s && a[child] < a[child + 1])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			swap(a[child], a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		JustDown(a, i, n);
	}

	int end = n - 1;

	while (end > 0)
	{
		swap(a[end], a[0]);
		JustDown(a,0,end);
		--end;
	}


}

交换排序

冒泡排序

冒泡排序：就是将两个相邻的元素进行比较，每次确定一个最值，然后得到有序序列。

冒泡跟选择一样，两个for循环就能搞定，每次循环都能确定一个最值，并将最值移动到数组的最后一个位置，然后第二次循环的时候，就不会在对最后一个位置进行比较。

---

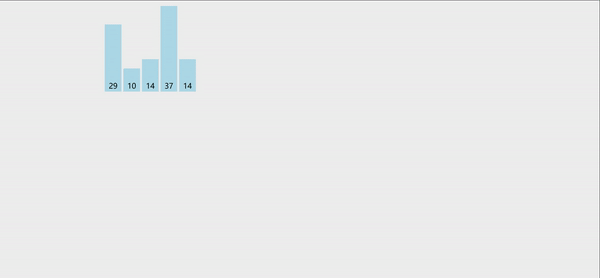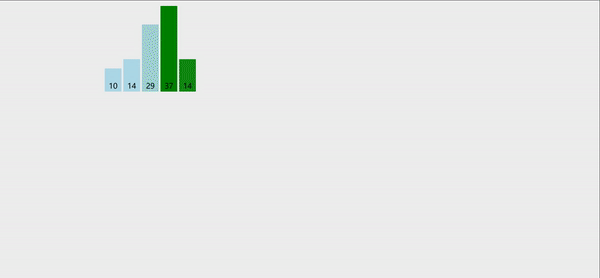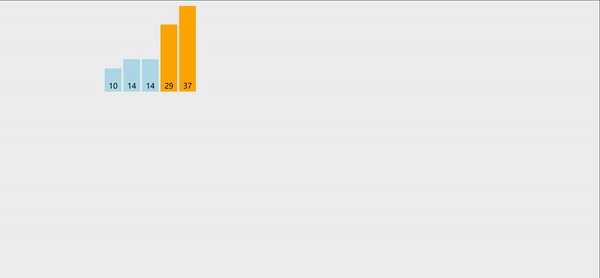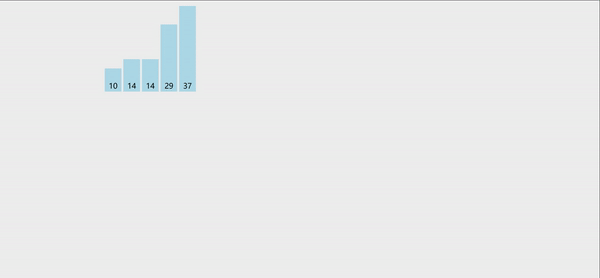
代码如下

void BubbleSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		for (int j = 0; j < n - i - 1; j++)
		{
			if (a[j + 1] > a[j])
			{
				swap(a[j + 1], a[j]);
			}
		}
	}
}

快速排序

快速排序是Hoare大佬于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

hoare版

left代表左边第一个元素，right代表右边第一个元素

1.找到一个基准值(key)

2.left向左移动，找到比key大的就停止

3.right向右移动，找到比key小的就停止

4.将left和right交换

5重复234操作，直到left对应的下标=right对应的下标就停止

---

代码如下

void PartSort1(int* a, int l, int r)
{
	if (l >= r)
	{
		return;
	}
	//取左边
	//int key_i = l;

	//随机取
	//int key_i = l + rand() % (r - l);

	//三数取中
	int key_i = GetNum(a, l,r);

	if (key_i != l)
	{
		swap(a[key_i], a[l]);
		key_i = l;
	}
	int begin = l;
	int end = r;

	while (l < r)
	{
		while (l < r && a[r] >= a[key_i])
		{
			r--;
		}

		while (l < r && a[l] <= a[key_i])
		{
			l++;
		}

		swap(a[l], a[r]);
	}

	swap(a[key_i], a[l]);
	key_i = l;

	PartSort1(a, begin, key_i - 1);
	PartSort1(a, key_i + 1, end);

}

可以用三数取中和随机选数来进行选择基准值上的优化

挖坑版

挖坑版也挺好理解的

1.先找一个基准值(key)，形成一个坑位(hole，hole是下标)

2.很hoare一样，left从左边开始移动，遇到比key大的就停止，然后将这个比key的数字填到坑里面，然后将坑hole的位置移动到left的位置，形成新坑

3.right从右边开始移动找小，然后将小的数字填在坑里面，坑的位置更新到right的位置

4.重复2和3，直到left==right

---

代码如下

void PartSort2(int* a, int l, int r)
{
	if (l >= r)
	{
		return;
	}

	int key = a[l];
	int hole = l;
	
	int bg = l;
	int ed = r;

	while (l < r)
	{
		while (l < r && a[r] >= key)
		{
			r--;
		}
		a[hole] = a[r];
		hole = r;
		
		while (l < r && a[l] <= key)
		{
			l++;
		}

		a[hole] = a[l];
		hole = l;
		
	}

	a[hole] = key;


	PartSort2(a, bg, hole - 1);
	PartSort2(a, hole + 1, ed);
}

前后指针法

1.依旧是选出一个基准值(key)

2.定义一个prev指向序列的开头，一个cur指向prev的下一个位置

3.若cur指向的数据小于key，则将prev向后移动，移动之后若prev和cur的位置没有重合，则将cur对应的数据和prev对应的数据进行交换，然后cur++，(不管prev移动不移动，cur都要向后移动)

4.重复第三步，直到cur <= 序列的有边界。

---

代码如下

void PartSort3(int* a, int l, int r)
{
	if (l >= r)
	{
		return;
	}

	int bg = l;
	int ed = r;

	int cur = l + 1;
	int prev = l;

	int key_i = l;

	while (cur <= r)
	{
		if (a[cur] < a[key_i] && ++prev != cur)
		{
			swap(a[cur], a[prev]);
		}
		++cur;
	}

	swap(a[prev], a[key_i]);


	PartSort3(a, bg, prev - 1);
	PartSort3(a, prev + 1, ed);
}

归并排序

归并排序