算法题——洛谷2

P8723 乘法表

题目描述

九九乘法表是学习乘法时必须要掌握的。在不同进制数下，需要不同的乘法表。

例如, 四进制下的乘法表如下所示：

1*1=1
2*1=2 2*2=10
3*1=3 3*2=12 3*3=21

请注意，乘法表中两个数相乘的顺序必须为样例中所示的顺序，不能随意交换两个乘数。

给定 $P$，请输出 $P$ 进制下的乘法表。

输入格式

输入一个整数 $P$。

输出格式

输出 $P$ 进制下的乘法表。$P$ 进制中大于等于 $10$ 的数字用大写字母 A、B、C、$\cdots$ 表示。

样例 #1

样例输入 #1

4

样例输出 #1

1*1=1
2*1=2 2*2=10
3*1=3 3*2=12 3*3=21

样例 #2

样例输入 #2

8

样例输出 #2

1*1=1
2*1=2 2*2=4
3*1=3 3*2=6 3*3=11
4*1=4 4*2=10 4*3=14 4*4=20
5*1=5 5*2=12 5*3=17 5*4=24 5*5=31
6*1=6 6*2=14 6*3=22 6*4=30 6*5=36 6*6=44
7*1=7 7*2=16 7*3=25 7*4=34 7*5=43 7*6=52 7*7=61

提示

对于所有评测数据, $2\le P\le 36$。

蓝桥杯 2020 第三轮省赛 AB 组 G 题。

def multiplication_table(p):
    for i in range(1, p):
        for j in range(1, i+1):
            product = i * j
            print("{}*{}={}".format(base_n(i, p),  base_n(j, p), base_n(product, p)),end=" ")
        print()


def base_n(num, n):
    """将十进制数字转换为n进制字符串"""
    if num == 0:
        return '0'
    digits = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
    result = ''
    while num > 0:
        result = digits[num % n] + result
        num //= n
    return result

n=int(input())
multiplication_table(n)

---

P8720 平面切分

题目描述

平面上有 $N$ 条直线, 其中第 $i$ 条直线是 $y=A_i\cdot x+B_i$ 。

请计算这些直线将平面分成了几个部分。

输入格式

第一行包含一个整数 $N$。

以下 $\mathrm{N}$ 行, 每行包含两个整数 $A_i,B_i$。

输出格式

一个整数代表答案。

样例 #1

样例输入 #1

3
1 1
2 2
3 3

样例输出 #1

6

提示

对于 $50\%$ 的评测用例, $1\le N\le 4,-10\le A_i,B_i\le 10$。

对于所有评测用例, $1\le N\le 1000,-10^5\le A_i,B_i\le 10^5$。

蓝桥杯 2020 第二轮省赛 B 组 I 题

def getnode(lines1, lines2):  # 得到两条直线交点，若平行，返回None
    A1 = lines1[0]
    B1 = lines1[1]
    A2 = lines2[0]
    B2 = lines2[1]
    if A1 - A2 == 0:
        return
    x = (B2 - B1) / (A1 - A2)
    y = A1 * x + B1
    x = round(x, 10)
    y = round(y, 10)
    return (x, y)

def main():
    n=int(input())
    list1=[]
    for _ in range(n):
        a, b = list(map(int, input().split()))
        list1.append((a, b))
    list1=list(set(list1))
    length=len(list1)
    set1 = set()
    ans=[1]*(length+1)
    for i in range(length):
        set1.clear()
        for j in range(i):
            node=getnode(list1[i],list1[j])
            if node==None: continue
            set1.add(node)
        ans[i]+=len(set1)
    print(sum(ans[:length])+1)

main()

---

P8707 走方格

题目描述

在平面上有一些二维的点阵。

这些点的编号就像二维数组的编号一样，从上到下依次为第 $1$ 至第 $n$ 行，从左到右依次为第 $1$ 至第 $m$ 列，每一个点可以用行号和列号来表示。

现在有个人站在第 $1$ 行第 $1$ 列，要走到第 $n$ 行第 $m$ 列。只能向右或者向下走。

注意，如果行号和列数都是偶数，不能走入这一格中。

问有多少种方案。

输入格式

输入一行包含两个整数 $n$，$m$。

输出格式

输出一个整数，表示答案。

样例 #1

样例输入 #1

3 4

样例输出 #1

2

提示

$1\le n,m\le 30$。

蓝桥杯 2020 第一轮省赛 A 组 G 题（B 组 H 题）。

def main():
    n,m=list(map(int,input().strip().split()))
    matrix=[[0]*(m+1) for _ in range(n+1)]
    matrix[1][1]=1
    for i in range(1,n+1):
        for j in  range(1,m+1):
            if (i&1 or j&1) and not (i==1 and j==1):
                matrix[i][j]=matrix[i-1][j]+matrix[i][j-1]
    print(matrix[n][m])

main()

---

P8682 等差数列

题目描述

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中 $N$ 个整数。

现在给出这 $N$ 个整数，小明想知道包含这 $N$ 个整数的最短的等差数列有几项？

输入格式

输入的第一行包含一个整数 $N$。

第二行包含 $N$ 个整数 $A_1,A_2,\cdots ,A_N$。（注意 $A_1\sim A_N$ 并不一定是按等差数列中的顺序给出 )。

输出格式

输出一个整数表示答案。

样例 #1

样例输入 #1

5
2 6 4 10 20

样例输出 #1

10

提示

包含 2,6,4,10,20 的最短的等差数列是 2,4,6,8,10,12,14,16,18,20。

对于所有评测用例，$2\le N\le 10^5$，$0\le A_i\le 10^9$。

蓝桥杯 2019 年省赛 B 组 H 题。

def main():
    n=int(input())
    list1=list(map(int,input().strip().split()))
    list1.sort()
    d=list1[1]-list1[0]

    for i in range(2,len(list1)):
        d=min(list1[i]-list1[i-1],d)
        if d == 0:
            print(n)
            return
    print((list1[-1]-list1[0])//d+1)
main()

---

P8681 完全二叉树的权值

题目描述

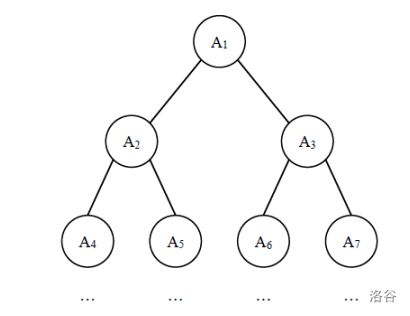
给定一棵包含 $N$ 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 $A_1,A_2,\cdots A_N$，如下图所示：

现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 $1$。

输入格式

第一行包含一个整数 $N$。

第二行包含 $N$ 个整数 $A_1,A_2,\cdots ,A_N$。

输出格式

输出一个整数代表答案。

样例 #1

样例输入 #1

7
1 6 5 4 3 2 1

样例输出 #1

2

提示

对于所有评测用例，$1\le N\le 10^5$，$0\le |A_i|\le 10^5$。

蓝桥杯 2019 省赛 A 组 F 题（B 组 G 题）。

n = int(input())
a = [0] + list(map(int, input().split()))

depth_sum = [0] * (n + 1)  # 存储每一层的权值和
for i in range(1, n+1):
    j = i.bit_length() - 1  # 当前节点的深度
    depth_sum[j] += a[i]  # 将当前节点的权值加到对应深度上

max_sum = max(depth_sum)  # 最大权值和
max_depth = depth_sum.index(max_sum) + 1  # 最大权值和对应的深度

print(max_depth)

---

P8668 螺旋折线

题目描述

如图所示的螺旋折线经过平面上所有整点恰好一次。

对于整点 $(X,Y)$，我们定义它到原点的距离 $\text{dis}(X,Y)$ 是从原点到 $(X,Y)$ 的螺旋折线段的长度。

例如 $\text{dis}(0,1)=3$，$\text{dis}(-2,-1)=9$。

给出整点坐标 $(X,Y)$，你能计算出 $\text{dis}(X,Y)$ 吗？

输入格式

$X$ 和 $Y$。

输出格式

输出 $\text{dis}(X,Y)$

样例 #1

样例输入 #1

0 1

样例输出 #1

3

提示

对于 $40\%$的数据，$-1000\le X,Y\le 1000$。

对于 $70\%$ 的数据，$-10^5\le X,Y\le 10^5$。

对于 $100\%$ 的数据，$-10^9\le X,Y\le 10^9$。

import math

x, y = map(int, input().split())  
m = max(abs(x), abs(y))  
d = 0

if y == -m:  
    d = m - x  
    d = -d  
elif x == m:  
    d = y + m  
else:  
    if y == m:  
        d = m - x + 2 * m  
    else:  
        d = m - y + 4 * m

print(4 * m * m + 2 * m - d)  

---

P8649 k 倍区间

题目描述

给定一个长度为 $N$ 的数列，$A_1,A_2,\cdots A_N$，如果其中一段连续的子序列 $A_i,A_{i+1},\cdots A_j(i\le j)$ 之和是 $K$ 的倍数，我们就称这个区间 $[i,j]$ 是 $K$ 倍区间。

你能求出数列中总共有多少个 $K$ 倍区间吗？

输入格式

第一行包含两个整数 $N$ 和 $K$$(1\le N,K\le 10^5)$。

以下 $N$ 行每行包含一个整数 $A_i$$(1\le A_i\le 10^5)$。

输出格式

输出一个整数，代表 $K$ 倍区间的数目。

样例 #1

样例输入 #1

5 2
1  
2  
3  
4  
5

样例输出 #1

6

提示

时限 2 秒, 256M。蓝桥杯 2017 年第八届

n, k = map(int, input().split())
a = [int(input()) for _ in range(n)]

c = [0] * k  # 余数计数器
c[0] = 1    # 处理整个序列都是K的倍数的情况

s = 0   # 前缀和
ans = 0 # 统计答案
for i in range(n):
    s += a[i]
    mod = s % k
    ans += c[mod]   # 统计贡献
    c[mod] += 1     # 更新余数计数器

print(ans)

或

n, k = map(int, input().split())
a = [int(input()) for i in range(n)]

# 用字典记录前缀和的余数出现的次数
s = {0: 1}  # 前缀和为 0 的出现次数为 1
sum_mod_k = 0
for i in range(n):
    sum_mod_k = (sum_mod_k + a[i]) % k
    if sum_mod_k in s:
        s[sum_mod_k] += 1
    else:
        s[sum_mod_k] = 1

# 计算所有 K 倍区间的个数
ans = 0
for x in s.values():
    ans += x * (x - 1) // 2  # 从 x 个中选出 2 个的组合数
print(ans)