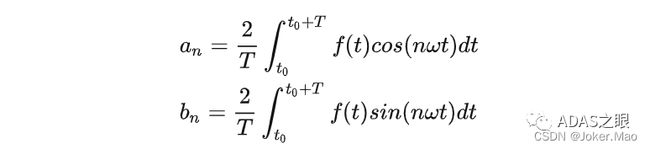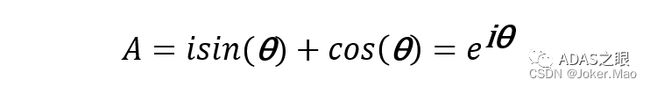信号与系统之《一文看懂傅里叶变换》
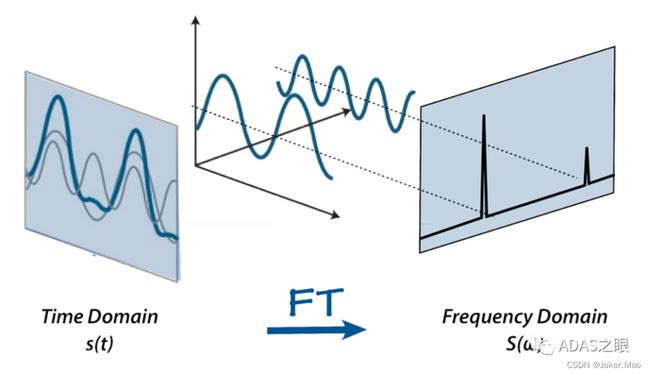
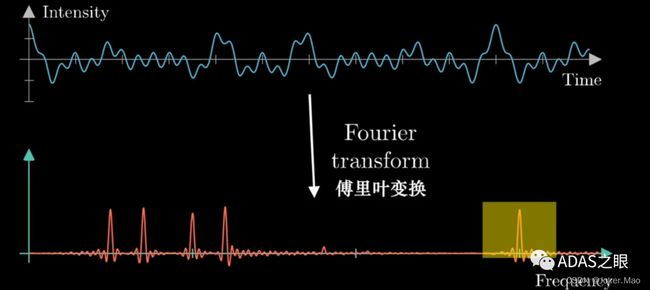
“傅里叶变换是一种非常有用的数学工具,它可以将一个复杂的信号分解成许多简单的频率成分。傅里叶变换在信号处理、图像处理、音乐、视频和通信等许多领域都有广泛的应用。相信大部分同学在毕业之后的一段时间之内都还没有理解到傅里叶变换的精髓,今天我们用通俗的案例讲解其背后的原理。”
基础回顾
1.1 基
回想一下线性代数中基的定义:
空间中一组特殊的向量,空间的每一个向量都可以由基向量唯一线性表示。
听起来其定义很简单,实际也很简单。以实际为例,考虑x-y正交坐标系,其中a点坐标(2, 3),b点坐标(5, 3),c点坐标(3, 0),如下图所示:
那么b点可以由a以及c进行唯一的表示:
b = a + c
当然c也可以由a&b作为基向量进行表示,a也可以由b&c作为基向量唯一的表示,也就是说上图中
1.2 标准正交基
——
什么是标准正交基呢?
首先,标准正交基也是基的一种,它也可以唯一地表示出线性空间中任意的一个向量;
其次,从几何意义上讲,正交的含义即两个向量垂直,也就是说假如向量a,以及向量b是正交的,那么a*b = |a||b|cosθ=0;
最后,标准的含义即标准正交基的向量模都是1。
线性空间中符合上述要求的一组基即称之为标准正交基。
我们还是以正交坐标系x-y为例,其x轴以及y轴上的单位向量分别为ex (1, 0)以及ey (0, 1),如下图所示:
图片
那么,我们可以得到如下关系:
a = 2 * ex + 4 * ey
b = 5 * ex + 3 * ey
扩展一下,x-y坐标系中的任意一个点p (m, n)都可以使用ex以及ey进行表示:
p = m * ex + n * ey
这里ex、ey便符合标准正交基的三个条件,因此
傅里叶变换
2.1 傅里叶级数
——
回想一下傅里叶级数定义,周期信号f(t)的傅里叶级数形式如下:
其中:
可以看出傅里叶级数的含义就是任意一个周期性函数都可以用一个垂直分量以及正余弦函数进行表示,思考一下我们第一章讲的基的定义,本质上:
<1,
上式就是一组基,这里的sin(nwt)以及cos(nwt)是每个都是一组(n属于0~∞),另外基的模都是1且互相正交,注意这里取模以及正交计算都是使用积分形式,这就是f(t)在线性空间的一组标准正交基。
这里我们为了更加直观的演示上面这组基中互相正交,我们使用python生成一组sin(w)以及sin(2w)相乘的图像:
x = np.linspace(-(4*np.pi),(4*np.pi),2048,endpoint=True)
a = np.sin(x)
b = np.sin(2*x)
c = a * b
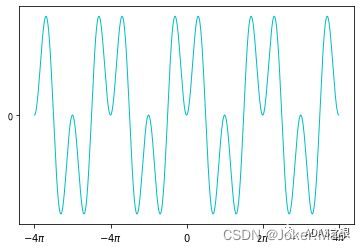
生成图像如下:
可以看出,sin(w)*sin(2w)是一个关于x轴上下对称的周期函数,我们对上面图像做积分可以得到:
sum = 0
for it in c:
sum = sum + it
print (int(sum))
0
另外一个方面,任意一个周期函数,都可以使用这组基进行唯一的表示。
另外,我们还可以将cos以及sin进行三角函数合成,则有:
考虑一段实际的波形:
f(t) = sin(t)+2sin(2t+π/2)
从式子中我们可以知道f(t)的傅里叶级数:
a0 = 0, a1 = 1, a2 = 2, an = 0 (n > 2)
另外,每个频率的对应的相位分别为:
ψ2 = π / 2, ψn = 0 (n != 2)
更加直观的,我们使用python将f(t)以及其正弦子图像展示如下:
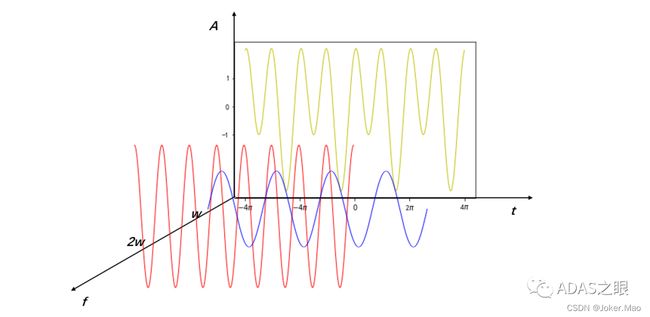
但上图中无法看出相位,我们再将其拓展旋转下:
这里便可以很清楚的看出f(t)是由那些频率的正弦信号组成,以及正弦信号的相位是多少。反过来,我们知道了频率以及相位图,我们还可以反推出原来的f(t)。
2.2 傅里叶变换
——
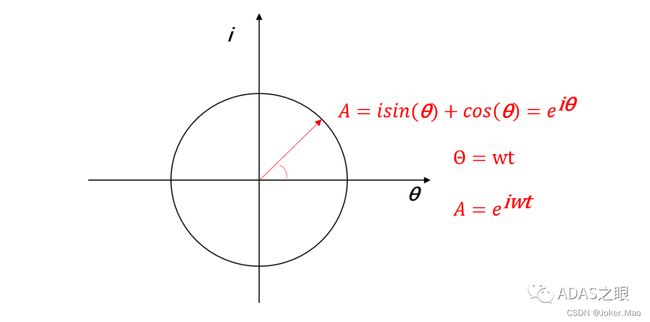
考虑欧拉坐标系上的一点A,角度为θ,如下图所示:
那么其可以表示为上面的点A可以表示为:
注意的是这里的sin以及cos是一组标准正交基,现在假如A点以角度w进行转动,那么A点可以表示为:
这里A的含义即围绕着原点逆时针进行转动,而e^-iwt则是让A点顺时针以w的角速度进行转动,需要注意的是,A点是由标准正交基sin以及cos组成的。
现在,我们引入傅里叶变换:
当f(t)中不含有w频率的正弦分量的时候,此时由于e^-iwt中的sin(w)与其他的正交基相乘,此时F(w)=0;
当f(t)中含有sin(w)分量时,此时F(w)非0,但要注意F(w)是个负数,还有虚部,其虚部即相位的偏移。
2.3 傅里叶变换应用
——
信号处理:
傅里叶变换在信号处理领域中被广泛应用,例如图像处理、音频处理等。它可以将一个时域信号转换为一个包含该信号中频率信息的频域信号,从而方便对信号进行分析和处理。
通信系统:
傅里叶变换可以用来分析和设计通信系统中的滤波器、调制器和解调器等组件。通过将信号转换为频域信号,我们可以更好地理解信号在系统中的传输和处理过程,并且可以优化系统的性能。
物理学和工程学:
傅里叶变换在物理学和工程学中也有广泛的应用。例如,在电路分析中,傅里叶变换可以用来计算电路中的频率响应。在信号处理和控制系统中,傅里叶变换可以用来设计滤波器和控制器等。
图像处理:
傅里叶变换可以将图像转换为频域表示,从而可以进行滤波、增强、压缩和分析等操作。通过使用傅里叶变换,我们可以将图像中的不同频率的信息分离出来,并对这些信息进行处理和分析。
结束语
傅里叶变换虽然看起来有些抽象和复杂,但是它的应用却是非常广泛而且实用的。从通信、图像处理、音频处理到物理学和化学等领域,傅里叶变换都有着不可替代的地位。希望通过本文,您能够更加深入地了解傅里叶变换及其在数学、物理、工程等领域中的重要应用。如果您对这个话题还有任何疑问或者想要了解更多,欢迎在评论区留言或者私信我。感谢您的关注,我们下期再见!