SPR:SUPERVISED PERSONALIZED RANKING BASED ON PRIOR KNOWLEDGE FOR RECOMMENDATION
1.摘要
推荐系统的目标是通过用户-项目交互历史来建模每个用户和每个项目之间的相关性,从而最大化正样本分数,最小化负样本。目前,两种流行的损失函数被广泛用于优化推荐系统:点态和成对。虽然这些损失函数被广泛使用,但是,存在两个问题。
(1) 这些传统的损失函数不能充分满足推荐系统的目标,也不能充分利用先验知识信息。(2) 这些传统损失函数的收敛速度较慢,使得各种推荐模型难以实际应用。
为了解决这些问题,我们提出了一种新的损失函数,称为基于先验知识的监督个性化排序(SPR)。该方法利用原始数据中每个用户或项目交互历史的先验知识,改善了BPR损失。与BPR不同的是,该SPR不是构造<用户,正项,负项>三元组,而是构造<用户,相似用户,正项,负项>四元组。虽然SPR非常简单,但它非常有效。大量实验表明,我们提出的SPR不仅实现了更好的推荐性能,而且显著加快了收敛速度,从而显著减少了所需的训练时间。
2.引言
随着互联网技术的发展,信息过载问题日益严重。推荐系统是一种信息过滤器,用于呈现用户可能感兴趣的内容。推荐系统通常使用嵌入向量来表示用户和项目。其基本思想是,具有相似交互历史的用户具有相似的兴趣和偏好,即相似节点的嵌入应该在嵌入空间中彼此接近。
为了学习有价值和可靠的嵌入向量,人们对推荐系统中的损失函数进行了大量研究。推荐系统中广泛使用的损失函数可分为两类:点损失函数和成对损失函数[12]。逐点损失函数,如均方误差(MSE)、二进制交叉熵(BCE)直接拟合每个样本的标签。Koren等人使用MSE优化其矩阵分解模型[13]。薛等人考虑了显式评分和内隐反馈,以改善BCE,从而优化其模型[9]。何等人使用BCE损失函数优化了他们的NeuMF模型,并取得了良好的效果。后果此外,行业中有许多模型使用逐点损失函数优化其模型
虽然逐点损失函数简单有效,但它只能优化单个交互,而没有排名信息,这不利于推荐系统生成推荐列表。为了解决这个问题,提出了成对损失函数,如BPR和协作度量学习(CML)。王等人使用BPR优化了他们的NGCF模型。他等人使用BPR优化了lightGCN模型,取得了良好的结果。Tay等人使用CML优化其LRML模型。
虽然这些损失函数已经取得了广泛的成功,但它们存在两个缺点:
上述损失函数没有充分利用原始数据的先验知识。具体来说,传统的损失函数直接对观察到的隐式交互数据建模,而忽略了交互数据中的先验知识。利用这些先验知识,我们可以有目的地让具有相似交互历史的用户或项目学习相似的表示,以提高推荐性能。此外,直接模拟观察到的隐式交互的传统损失函数实际上是模拟实际点击率,而不是用户和项目之间的相关性,因为用户和项目之间的交互意味着用户在对项目感兴趣的同时观察项目。当用户和项目之间没有交互时,并不意味着用户对项目不感兴趣。
上述损失函数没有充分利用先验知识,导致其训练效率低,这使得推荐模型的实际应用非常困难。具体来说,以LightGCN为例,需要1000个历元作为最优参数才能收敛。使用GTX3090进行训练时,训练过程大约需要36小时。
为了解决上述问题,我们提出了一种基于先验知识的监督个性化排序(SPR)损失。其设计动机与我们之前的工作(推荐的监督对比学习)[18]一致。也就是说,具有相似交互历史的节点应该具有相似的表示,这符合推荐系统的动机。我们之前的工作表明,利用这些先验知识可以有效地提高表示质量,从而提高推荐性能。
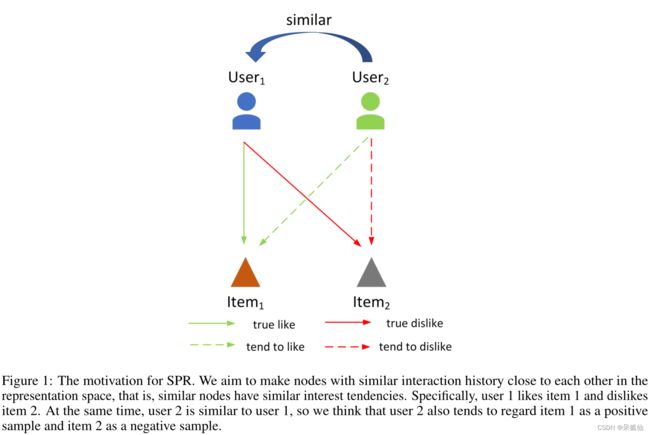
具体来说,如图1所示,SPR的设计动机是使用原始数据的先验知识来考虑具有相似交互历史的用户也具有相同的兴趣倾向,以便相似节点的表示可以彼此接近。即使用户b和项目i之间没有交互,我们仍然将其视为正样本对,并将用户b和项目j视为负样本对。我们认为,这种建模方法可以模拟用户的兴趣趋势,而不是点击率,而不是直接与点击历史进行交互建模。为了实现SPR,我们采用了动态采样的方法来提高采样效率。
此外,与传统的损失函数相比,由于SPR利用了更多的先验知识,因此SPR的收敛速度显著加快。这降低了一些复杂推荐模型(如图神经网络)的实际应用难度。
值得注意的是,尽管SPR的动机很简单,但它非常有效。SPR可以简单直接地应用于过去提出的各种推荐系统的骨干网络,以取代BPR等损失函数。
综上所述,本文的主要贡献总结如下:
我们提出了一种新的损失函数,称为基于先验知识的监督个性化排名损失,该函数利用原始数据的先验知识来建模用户的兴趣趋势,提高学习表示的质量,并提高推荐性能。
由于所提出的SPR利用了更多的先验知识并依赖于动态采样方法,因此其收敛速度大大加快,从而降低了复杂模型的实际应用难度。
我们在各种广泛使用的损耗函数和骨干网络上进行了充分的对比实验。实验结果表明,该SPR损耗具有优越的性能。
本文的其余部分组织如下。第2节成对和成对损失函数的详细信息。在第3节中,我们详细介绍了SPR的细节和实现。在第4节中,对各种损耗函数和骨干网络进行了大量实验,证明了所提出的SPR的有效性和效率。最后,在第5节中得出结论。
2.准备工作
2.1.问题陈述
用户-项目交互集可以很容易地建模为二部图 G = ( U , V , ξ ) G=(U,V,\xi) G=(U,V,ξ),其中 U U U表示用户集, V V V表示项目集, ξ \xi ξ表示边集。如果用户和项目之间存在交互,那么它们之间就有一条边。推荐系统需要嵌入每个用户 i ∈ U i\in U i∈U和项目 j ∈ V j\in V j∈V转化为统一的 d d d维表示空间,相应的表示用 u ∈ d u\in^d u∈d和 v ∈ d v\in ^d v∈d,使用嵌入式表示,推荐系统可以通过评分函数确定用户对某个项目的兴趣,从而决定是否应该向用户推荐该项目。推荐系统的目的是使阳性样本对的分数尽可能大,而阴性样本对的分数尽可能小。
2.2.逐点损失
逐点损失函数直接优化观察到的交互,即优化观察到的用户项交互和基本真相标签。典型的点态损耗函数是MSE损耗函数和BCE损耗函数。均方误差损失函数的形式如下[20,21]:

其中 M M M是交互总数, y ^ u i \hat y_{ui} y^ui是用户 u u u和项目 i i i的推荐模型的预测分数, y ^ u i \hat y_{ui} y^ui是用户 u u u和项目 i i i的实际分数。 λ \lambda λ是控制L2正则化强度的参数。MSE损失函数直接建模预测结果和标签的误差,并通过最小化该误差来优化推荐的模型参数。
与MSE损失(将优化目标视为回归任务)不同,BCE损失将优化目标视为分类任务,其形式如下[5]:
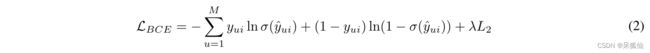
虽然逐点损失函数可以取得良好的效果,但其优化过程中不包含排名信息,这不利于推荐模型生成推荐列表。一般来说,两两损失函数比点损失函数可以获得更好的结果。
2.3.成对损耗
成对损失函数通常选择<用户,正项,负项>形成三元组,其中正项表示项目已与用户交互,负项表示项目未与用户交互。成对损失函数的优化目标是使用户和积极项的得分高于用户和消极项的得分。典型的成对损失函数包括BPR、CML。BPR的损失函数如下[15]:

其中 N u N_u Nu表示用户 i i i的正项目集。BPR可以使正对得分大于负对,从而提高推荐模型的性能。
与BPR直接优化用户-项目对得分不同,CML的优化目标是表示空间中用户和项目之间的距离,其形式如下:
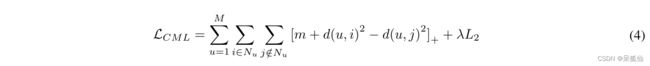
其中, d ( a , b ) 2 d(a,b)^2 d(a,b)2表示节点 a a a和节点 b b b之间的欧几里得距离, [ z ] + = m a x ( z , 0 ) [z]+=max(z,0) [z]+=max(z,0)表示标准铰链损耗。此外,CML损耗还包括特征损耗,有关CML的详细信息见[16]。
虽然成对损失函数的性能非常好,但我们认为上述损失没有充分利用原始交互历史数据的先验知识。此外,我们认为上述损失函数不能充分表达用户和项目之间的相关性。因此,我们提出了SPR损耗函数。
3.方法
3.1.SPR管道
我们提出SPR的原因是传统的损失函数不能充分模拟用户的兴趣趋势。具体来说,对于用户 i i i和项目 j j j,存在交互变量 Y i j Y_{ij} Yij、相关变量 R i j R_{ij} Rij和观察变量 O i j O_{ij} Oij。当用户和项目之间存在交互时, Y i j = 1 Y_{ij}=1 Yij=1,否则为 0 0 0,当用户与项目相关时, R i j = 1 R_{ij}=1 Rij=1,否则为 0 0 0,当用户观察项目时, O i j = 1 O_{ij}=1 Oij=1,否则为 0 0 0。只有当用户 i i i与项目 j j j相关并且存在观察行为时,才会发生交互行为。具体而言,数学形式为:
![]()
这意味着传统的损失函数模型是交互变量 Y i j Y_{ij} Yij,而不是相关变量 R i j R_{ij} Rij。因为在历史交互数据中,我们只能直接观察交互历史,而不能观察相关性。此外,传统的损失函数没有充分利用先验知识,它们只利用用户-项目关系信息,而不是用户-用户关系信息。
为了解决上述问题,本文提出了SPR损耗函数。SPR不仅利用了用户-项目关系信息,而且充分考虑了先验知识约束下的用户-用户关系。具体来说,SPR不是构建 < u s e r , p o s i t i v e i t e m , n e g a t i v e i t e m >
SPR遵循推荐系统的基本思想,即具有相似交互历史的用户具有相同的兴趣倾向。因此,我们认为 u s e r l user_l userl与 u s e r i user_i useri具有相同的兴趣倾向, u s e r i user_i useri的正样本被视为 u s e r l user_l userl的正样本,即使它们之间没有真正的交互。同样, u s e r i user_i useri的负样本被视为 u s e r l user_l userl的负样本。
为了引入原始交互数据的先验知识,SPR首先需要计算每个用户之间的相似度,相似度计算的矩阵形式如下:
![]()
其中 G G G是表示每个用户的交互历史的稀疏矩阵 ∣ G ∣ |G| ∣G∣表示矩阵的行归一化。在计算相似性之后,我们对每行 S S S进行排序,并选择前 k k k%最相似的用户。
然后,我们将对每个节点进行排序,并选择前 k k k%的节点作为可用于替换的类似节点。值得注意的是,在计算相似度时,分别计算用户端节点和项目端节点。假设整个交互历史中有 N N N个用户,那么对于每个用户 t t t,我们将选择 N ∗ k N∗ k N∗k%的用户与 u s e r t user_t usert的类似用户。
然后,SPR损耗可以计算为:
![]()
其中, Y u i = 1 , Y u j = 1 , l Y_{ui}=1,Y_{uj}=1,l Yui=1,Yuj=1,l是通过等式6获得的 i i i的随机相似用户。 l l l不需要与项目 i i i和项目 j j j进行特定交互。 D D D代表SPR的训练集。
可以观察到,在损失函数中,我们不仅考虑了用户项目关系侧,而且还考虑了用户-用户关系侧。用户-用户关系方面的信息来自历史交互数据的先验知识,这使得模型能够使用更多信息进行学习,并加快了模型的收敛速度。此外,SPR没有直接建模观察到的交互,而是将没有交互的用户项目对视为正样本,这使得SPR学习的嵌入更可能代表用户的兴趣,而不是点击率。
3.2.SPR取样
由于SPR需要同时使用用户 i i i和相似用户 l l l来计算损耗,因此如何对数据进行采样对于SPR的应用至关重要。一种直观的方法是将用户 i i i的所有相似用户分组为用户对,并集体计算损失。然而,这将在大规模数据集上带来巨大的计算成本,这不符合SPR提高模型收敛速度的目的[22]。为了保证SPR的训练效率,我们遵循BPR动态采样的基本思想,在SPR上实现了动态采样[17,23,15]。SPR采样的具体步骤如下。

3.3.SPR的复杂性分析
与BPR相比,SPR将从三个方面增加计算复杂度。首先,计算用户交互历史的相似性。假设数据集中有 N N N个用户,矩阵乘法的复杂度为 O ( N 3 ) O(N^3) O(N3),排序的复杂度为 O ( l o g 2 N 2 ) O(log_2N^2) O(log2N2)。当执行动态采样时,SPR和BPR的复杂度在同一个数量级,即 O ( N ) O(N) O(N)。假设BPR采样所需的计算复杂度为 O ( ϑ ) O(\vartheta) O(ϑ),则SPR采样所需的计算复杂度为 O ( ϑ ∗ γ ) O(\vartheta∗\gamma) O(ϑ∗γ). 在计算损失函数时,SPR也与BPR处于相同的数量级。假设BPR在计算损耗时的计算复杂度为 O ( τ ) O(\tau) O(τ),则SPR的计算复杂度为 O ( 2 ∗ τ ) O(2∗\tau) O(2∗τ).。通常,SPR的额外计算可以表示为:![]()
值得注意的是,相似矩阵的计算是在数据预处理阶段进行的,这意味着SPR在模型部分的计算成本是BPR的一个数量级。
4.实验
我们首先在第4.1节中说明了实验设置,包括数据集、评估指标和实现细节。接下来,我们在第4.2节中对各种不同的损耗函数和骨干网络进行了广泛的比较实验。最后,我们在第4.3节中对SPR的应用进行了进一步的研究。
4.1.1.数据集
top-K推荐采用了Gowalla[24,25]、Yelp2018[26,17]和Amazon Book[27]三个公共推荐数据集,以验证SPR的有效性。为了确保实验中不同条件的一致性和公平性,在不同条件下使用的训练集和测试集与LightGCN论文[17]中使用的训练集和测试集完全相同。三个数据集的具体统计数据如表1所示。
4.1.2.实验指标
在top-k推荐中,我们实现了[26]中描述的策略和[26]中描述的排序协议。采用归一化贴现累积增益(NDCG)和召回作为推荐性能指标来评估推荐性能。我们考虑K为20的情况,因为使用了LightGCN纸[17]。
4.1.3.实施细节
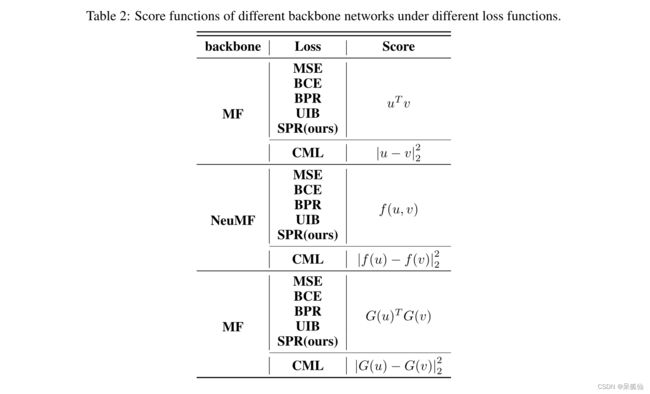
在这里,我们比较了三种不同主干网络上的六种损耗函数。六个损失函数是MSE[13]、BCE[5、2、1]、BPR[25、15、17]、CML[16]、用户兴趣边界(UIB)[28]、SPR(ours)。这三个骨干网络是MF[13]、NeuMF[5]和LightGCN[17]。
具体而言,MSE、BCE、BPR和CML的损失函数分别由公式1、2、3和4获得。UIB的损失函数具有以下形式:

其中 ϕ \phi ϕ表示 l n σ ln\sigma lnσ, b u b_u bu表示用户 i i i的个性化决策边界,可计算如下:
![]()
其中, W T W^T WT是每个用户共享的可学习参数, u i u_i ui是用户 i i i的推荐模型输出的嵌入向量。UIB结合了点态损失函数的灵活性和成对损失函数的优点进行排序,可以为每个用户学习个性化的决策边界,并取得了良好的效果。
MF是基本的协同过滤模型,它用嵌入向量表示每个用户和项目。它通过矩阵分解优化嵌入表示。MF通过嵌入向量的内积直接计算用户和项目之间的相关性,并生成推荐列表。
NeuMF是一种基于深度学习的协同过滤模型。它不仅保留了通过矩阵分解优化嵌入的部分,而且提出了通过MLP优化嵌入的网络部分。NeuMF将用户和项目作为输入,并直接通过线性层输出预测分数。
LightGCN是一种基于图神经网络的协同过滤算法。LightGCN考虑当前节点的域,通过信息传递和聚合更新当前节点的嵌入向量。它通过多次迭代获得节点的高阶字段信息。LightGCN使用嵌入向量的内积来预测用户和项目分数。
值得注意的是,CML损失函数需要嵌入来计算每个节点之间的欧几里德距离。将CML应用于NeuMF,我们将最后一个线性层的输入作为节点的嵌入表示。此外,CML优化了表示的欧几里得距离,因此其预测分数也由用户和项目之间的欧几里得距离决定。嵌入距离越远,其得分越低。
具体而言,不同条件下的得分函数如表2所示。
公平地说,所有模型的嵌入大小都固定为64,嵌入参数用Xavier方法初始化[29]。用于所有模型的优化器是Adam[30]。批量大小设置为1024,L2正则化常数 λ \lambda λ设置为 1 e − 4 1e^{−4} 1e−4,对于所有模型和损失函数,学习率设置为0.001。对于SCL特有的参数,我们进行了单独的探索。 γ \gamma γ在{4,5,6,7,8,10,12,15,20}范围内搜索。将SPR与其他模型进行比较时, γ \gamma γ设置为10。
4.2.性能比较
我们在Gowalla、Yelp2018和Amazon Book数据集上比较了SPR与MSE、BCE、BPR、CML和UIB,并将MF、NeuMF和LightGCN作为主干,结果如表3所示。在表中,最佳性能用粗体标出,次优性能用下划线标出。平均改进表示SPR在三个主干网络上相对于次优结果所实现的相对性能改进。

从不同损失函数的角度来看,从表中可以看出,我们提出的SPR应用于三个骨干网络,在不同的数据集上实现了一致的改进。对于Gowalla、Yelp2018和Amazon book,与次优损失函数相比,召回结果分别提高了0.86%、3.15%、6.08%,ndcg结果分别提高了1.44%、3.40%、7.55%。此外,由于SPR是在BPR的基础上改进的,因此有必要直接将SPR与BPR进行比较。与次优损失函数相比,召回结果平均分别提高了1.64%、6.50%、9.02%,ndcg结果分别提高了1.79%、5.13%、10.54%。可以看出,与BPR相比,SPR利用了原始数据的先验知识,通过建立四元组可以利用更多的用户信息,并取得了非常显著的改进。值得注意的是,对Gowalla数据集的改进相对较小。我们认为这是因为Gowalla较小的数据规模使得在建立用户关系时更难引入多样性,这使得SPR可以使用比Amazon book更少的信息。这表明SPR非常适合在相对较大的数据集上应用。
从骨干网络的角度来看,从表中可以看出,我们提出的SPR在所有骨干网络上都实现了一致的改进。无论是传统的矩阵分解模型、神经网络模型还是图卷积网络模型,SPR都可以非常简单地应用于改善效果。这充分证明了SPR的灵活性和可转移性。此外,我们还可以注意到,SPR在不同骨干网络上的性能改善率相似。这意味着SPR不依赖于骨干网络的特征提取能力,SRP可以稳定地实现性能改进。
简而言之,我们可以从表3中看到。SPR在所有数据集和所有骨干网络上实现了稳定的性能改进。SPR的性能与数据集的关系更大,与骨干网络的关系较小。
为了充分说明SPR在收敛速度方面的优势,我们将召回和ndcg的趋势与不同损失函数下的训练过程进行了比较。通过测试召回和测试每20个时期的ndcg评估的列车曲线如图2所示。为了节省空间,我们只显示了基于LightGCN的每个损失函数的训练曲线,而忽略了MF和NeuMF的结果,这与LightGCN的趋势相同。
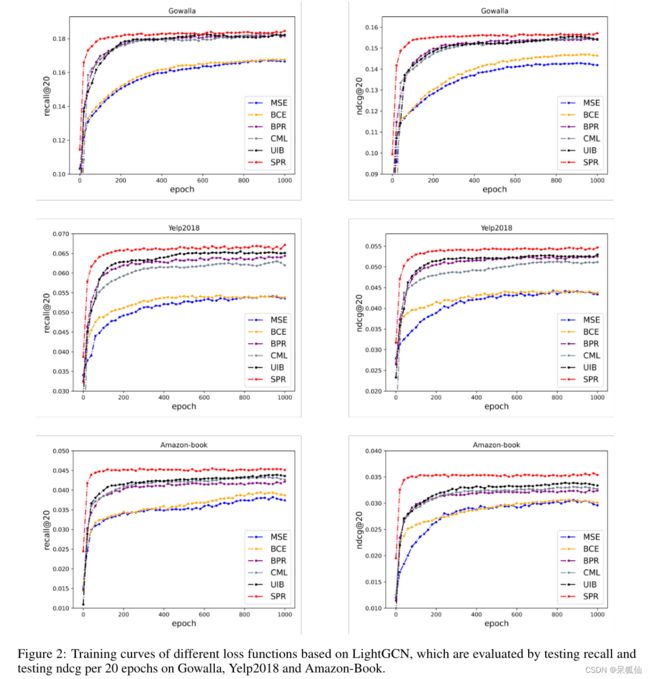
如图2所示,我们可以观察到,我们提出的SPR的收敛曲线相当陡峭,这意味着SPR在收敛速度方面具有非常明显的优势。具体来说,BPR、UIB和CML通常需要1000个阶段来确保其收敛,在Gowalla数据集上通常分别需要40小时、48小时和54小时。虽然SPR需要更多的采样,但我们提出的SPR只需要大约100个历元就可以收敛到与BPR、UIB和CML类似的结果,只需要大约5个小时。这一优势在亚马逊图书数据集上更为明显,SPR只需要50个时代就可以超越BPR。
这是因为SPR使用先验知识来建立监督信息,并且可以使用用户项二部图的更多交互数据来建立用户-用户关系,从而在每次迭代中考虑更多信息,使收敛速度显著加快。
此外,从图2中还可以发现,随着SPR的进一步训练,推荐模型的性能进一步提高。这进一步说明了充分利用先验知识的重要性。SPR可以使推荐模型更好地收敛,学习更高质量的用户和项目表示,从而提高推荐性能。结合表3和图2中的结果,我们可以得出以下结论:(1)首先,SPR具有更好的推荐性能,优于传统的点态损失函数和成对损失函数以及一些新的损失函数。(2) SPR的收敛速度显著提高,只需几个小时即可使模型收敛到令人满意的性能。这使得一些复杂模型的实际应用更加容易。总之,SPR具有重要的应用价值。
4.3.SPR研究
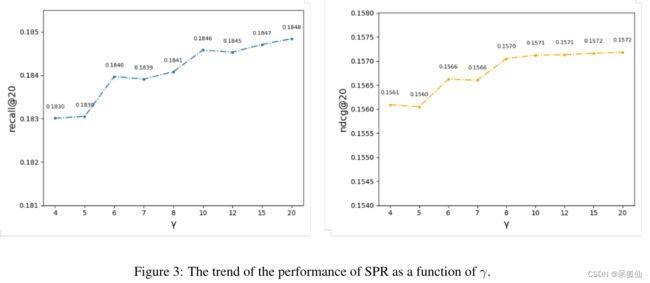
SPR的实现非常简单。与BPR相比,其唯一参数仅为采样率 γ \gamma γ。为了探索 γ \gamma γ对SPR的影响,在{4、5、6、7、8、10、12、15、20}范围内搜索 γ \gamma γ,结果如图3所示。为了节省空间,我们省略了在Yelp2018和Amazon book上的实验结果,这些结果显示出与Gowalla数据集相同的趋势。
从图3可以看出,随着 γ \gamma γ的增加,SPR的性能也会提高。然而,虽然较大的 γ \gamma γ将获得更好的性能,但过大的 γ \gamma γ将进一步增加采样复杂度和损失复杂度,这与我们提高模型收敛速度的目的背道而驰。因此,我们将 γ \gamma γ设置为10作为折衷方案,并建议在使用SPR时仔细调整 γ \gamma γ。
此外,如前所述,SPR与我们之前在监督下的推荐对比学习(SCL)工作相一致。其基本思想是充分利用用户项二部图的先验知识来构造监督信息,目的是使具有相似交互历史的用户或项目学习相似表示。因此,SCL和SPR的结合是一种非常自然的选择。
我们将SCL-SPR与NGCF[26]、LightGCN[17]、SGL[31]、SCL[18]进行了比较。选择这些模型作为基线的原因是,它们都是基于NGCF开发的,在同一标准上对它们进行比较是公平合理的。结果如表4所示。
如表所示,将SCL与SPR相结合可以明显改善SCL。与其他基线相比,SCL-SPR的性能优势明显。例如,与LightGCN相比,SCL-SPR在这三个数据集上的召回率分别增加了1.65%、7.82%、19.24%,ndcg分别增加了1.22%、8%和21.07%。SCL和SPR都利用先验知识构建监督信息,从而提高了性能。这充分证明了利用先验知识的有效性和必要性。

5.结论
在这项工作中,我们认识到传统损失函数没有充分利用先验知识的缺陷,并提出了一种新的损失函数,称为监督个性化排序。SPR利用用户项二部图交互历史的先验知识来构造监督信息,并在监督信息的指导下构造 < u s e r u , u s e r l , i t e m i , i t e m j >
在这项工作中,我们使用四元组来提高推荐性能。然而,SPR非常依赖于样本采样。如何进一步改善损失,使推荐损失能够在训练过程中考虑更多样本,是一个非常有趣的研究方向。
