带容量约束的p-中值选址问题建模与求解

带容量约束的p-中值选址问题建模与求解

1. 简介

选址理论的研究，最早始于1909 年，Weber 研究如何在平面上确定一个仓库位置，使仓库与顾客间的总距离最小(也称为 韦伯问题) ；而后在1964 年，Hakimi 提出了网络上的p-中值问题与p-中心问题，该研究在选址问题上具有里程碑意义，此后更多学者加入到选址理论的研究中。

目前选址问题主要有三类：
① P-中位问题（也称P-中值问题）：研究如何选择P个服务站使得需求点和服务站之间的距离与需求量的乘积之和最小，在物流领域应用得非常广泛；
②P-中心问题（也称 minmax 问题）：是探讨如何在网络中选择 P 个服务站，使得任意一需求点到距离该需求点最近的服务站的最大距离最小问题，在应急设施的选址上应用较广泛，如警局、消防局、医院等公共服务的选址，要求尽可能快到达；
③ 覆盖问题分为最大覆盖问题和集覆盖问题两类，集覆盖问题研究满足覆盖所有需求点顾客的前提下，服务站总的建站个数或建设费用最小的问题；最大覆盖问题是研究在备选物流中心里，如何选择p个设施，使得服务的需求点数最多或需求量最大。

2. p-中值问题建模与求解

2.1 场景构建

存在n个备选物流中心位置，m个需求点，要求从n备选物流中心中选取p个位置，使得各个需求点到物流中心的成本之和最低。

2.2 描述

优化目标：需求点到物流中心的距离与需求量的乘积之和最短；
约束条件：物流中心能力、需求点需求量、需求点只能由一个物流中心服务；
已知信息：备选物流中心位置、需求点位置、需求点需求量；
基本假设：运输成本与距离和货物量成正比。

2.3 数学模型

2.3.1 符号说明

2.3.2 数学模型

2.4 禁忌搜索算法设计

2.4.1 算法设计

2.4.1.1 编码

采用01编码和自然数编码组合的方式设计染色体，例如，有5个备选物流中心和17个需求点，从中选3个物流中心，编码设计为：[0, 1, 1, 0, 1, 1, 2, 1, 3, 3, 3, 3, 1, 2, 1, 2, 2, 1, 3, 1, 2, 3]，其中前五位[0, 1, 1, 0, 1]表示编号为0-4的备选物流中心是否被选，这里选出的第1、2、3个物流中心依次对应需要1、2、4号的备选物流中心被，而后面17位[1, 2, 1, 3, 3, 3, 3, 1, 2, 1, 2, 2, 1, 3, 1, 2, 3]对应需求点1-17，1、2、3表示由第1、2、3个物流中心服务，即对应备选物流中心序号的1、2、4。

2.4.1.1 禁忌搜索算法设计

禁忌搜索算法的核心思想是不重复已搜索过的解，以提高搜索效率。本算法在求解时主要设置两个禁忌表：全局禁忌表和局部禁忌表，在邻域搜索时采用随机成对交换两城市位置获取新的路径。其中全局禁忌表存储迭代过程中最近n代的结果（n为禁忌长度），局部禁忌表存储每一代领域搜索时遍历到的新路径，以实现全局禁忌（全局不重复搜索）和局部禁忌（邻域遍历不重复搜索）。

2.4.2 python程序设计

# -*- coding: utf-8 -*-
import math
import random
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 添加这条可以让图形显示中文


#计算路径距离，即评价函数
def calFitness(chrom,dis_matrix, cnum, d, c):
    dis_sum = 0
    dis = 0
    declist = []
    dec_chrom =chrom.copy()
    d_list = [[] for i in range(cnum)]
    weight = [0 for i in range(cnum)]
    demand = [0 for i in range(cnum)]
    
    for i in range(cnum):
        if chrom[i] == 1:
            declist.append(i)
    
    for i in range(cnum,len(dec_chrom)):
        dec_chrom[i] = declist[dec_chrom[i]-1]
        d_list[dec_chrom[i]].append(i-cnum)
        weight[dec_chrom[i]] += dis_matrix.loc[i-cnum,dec_chrom[i]]*d[i-cnum]
        demand[dec_chrom[i]] += d[i-cnum]
        
    
    dis_sum = 0 
    flag = 0
    for i in range(len(demand)):
        if demand[i] > c[i]:
            dis_sum = math.pow(10,10)
            flag = 1
            break
    if flag==0:
        dis_sum = sum(weight)
    return round(dis_sum,1)


def traversal_search(chrom,dis_matrix,tabu_list, cnum, d, c, p):
    #邻域随机遍历搜索，成对交换+单点变异
    traversal = 0#搜索次数
    traversal_list = []#存储局部搜索生成的解,也充当局部禁忌表
    traversal_value = []#存储局部解对应路径距离
    while traversal <= traversalMax:
        new_chrom = chrom.copy()#复制当前路径，并交换生成新路径
        pos1,pos2 = random.randint(0, cnum-1),random.randint(0, cnum-1)#交换点
        new_chrom[pos1],new_chrom[pos2]=new_chrom[pos2],new_chrom[pos1]
        
        pos1,pos2 = random.randint(cnum,len(chrom)-1),random.randint(cnum,len(chrom)-1)#交换点
        new_chrom[pos1],new_chrom[pos2]=new_chrom[pos2],new_chrom[pos1]
        
        for i in range(cnum,len(chrom)):
            if random.random() > 0.75:#一定概率改变
                new_chrom[i] = random.randint(1,p)
                
        new_value = calFitness(new_chrom,dis_matrix, cnum, d, c)#当前路径距离
        #新生成路径不在全局禁忌表和局部禁忌表中，为有效搜索，否则继续搜索
        if (new_chrom not in traversal_list) & (new_chrom not in tabu_list):
            traversal_list.append(new_chrom)
            traversal_value.append(new_value)
            traversal += 1
    
    return min(traversal_value),traversal_list[traversal_value.index(min(traversal_value))]
    
    
def initialize(dnum, cnum , p):
    """
    in:dnum-需求点数量，cnum-备选点数量，
    out:染色体
    """
    clist = random.sample(range(cnum),p)
    cchrom = [1 if i in clist else 0 for i in range(cnum) ]
    dchrom = [random.choices(range(1,p+1))[0] for i in range(dnum)]
    chrom = cchrom + dchrom
    
    return chrom
    
    
#画散点图
def draw_sca(Coordinates1,Coordinates2):
    x,y= [],[]
    
    x = [i[0] for i in Coordinates1]
    y = [i[1] for i in Coordinates1]
    plt.scatter(x, y, color='#ff69E1', marker='o')
    
    x = [i[0] for i in Coordinates2]
    y = [i[1] for i in Coordinates2]
    plt.scatter(x, y, color='#4169E1', marker='*')
    
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


#画分布图
def draw_path(chrom, demandCoordinates, centerCoordinates, p, cnum):
    centerlist = []
    for i in range(cnum):
        if chrom[i] == 1:
            centerlist.append(centerCoordinates[i])
    
    for i in range(cnum,len(chrom)):
        if chrom[i] == 1:
            plt.plot([centerlist[0][0],demandCoordinates[i-cnum][0]], [centerlist[0][1],demandCoordinates[i-cnum][1]], 'r-', color='#4169E1', alpha=0.8, linewidth=0.8)#plt.plot([x1,x2],[y1,y2])
        elif chrom[i] == 2:
            plt.plot([centerlist[1][0],demandCoordinates[i-cnum][0]], [centerlist[1][1],demandCoordinates[i-cnum][1]], 'r-', color='#4169E1', alpha=0.8, linewidth=0.8)
        elif chrom[i] == 3:
            plt.plot([centerlist[2][0],demandCoordinates[i-cnum][0]], [centerlist[2][1],demandCoordinates[i-cnum][1]], 'r-', color='#4169E1', alpha=0.8, linewidth=0.8)
    draw_sca(demandCoordinates,centerCoordinates)


if __name__ == '__main__':
    #参数
    CityNum = 50#城市数量
    MinCoordinate = 0#二维坐标最小值
    MaxCoordinate = 100#二维坐标最大值
    
    #TS参数
    tabu_limit = 100 #禁忌长度
    iterMax = 1000#迭代次数
    traversalMax = 100#每一代局部搜索次数
    
    tabu_list = [] #禁忌表
    tabu_time = [] #禁忌次数
    best_value = math.pow(10,10)#较大的初始值，存储最优解
    best_line = []#存储最优路径
    
    #需求点位置及需求量，备选中心位置及能力
    demandCoordinates = [(88, 16),(25, 76),(69, 13),(73, 56),(80, 100),(22, 92),(32, 84),(73, 46),(29, 10),(92, 32),(44, 44),(55, 26),(71, 27),(51, 91),(89, 54),(43, 28),(40, 78)]
    centerCoordinates = [(32, 60),(69, 33),(49, 40),(72, 81),(61, 65)]
    d = [3,4,5,6,7,4,2,3,4,5,6,3,5,4,3,5,1]#需求量，对应demandCoordinates
    c = [25,25,25,25,25]#能力都设置为25，对应centerCoordinates
    
    draw_sca(demandCoordinates,centerCoordinates)#位置图
    
    p = 3 #待决策物流中心数量
    dnum = len(demandCoordinates) #需求点数量
    cnum = len(centerCoordinates) #备选中心数量
    
    
    # 计算中心与需求点之间的距离
    dis_matrix = pd.DataFrame(data=None,columns=range(cnum),index=range(dnum))
    for i in range(dnum):
        xi,yi = demandCoordinates[i][0],demandCoordinates[i][1]
        for j in range(len(centerCoordinates)):
            xj,yj = centerCoordinates[j][0],centerCoordinates[j][1]
            dis_matrix.iloc[i,j] = round(math.sqrt((xi-xj)**2+(yi-yj)**2),2)
    
    
    # 初始化,随机构造
    num = 50
    chroms = [initialize(dnum, cnum, p) for i in range(num)]
    values = [calFitness(chrom,dis_matrix, cnum, d, c) for chrom in chroms]
    
    best_value = min(values)
    best_chrom = chroms[values.index(best_value)]
    chrom,value = best_chrom,best_value
    
    # 存储当前最优
    print('初代最优值 %.1f' % (best_value))
    
    best_value_list = []
    best_value_list.append(best_value)
    #更新禁忌表
    tabu_list.append(best_chrom)
    tabu_time.append(tabu_limit)
    
    itera = 0
    while itera <= iterMax:
        new_value,new_chrom = traversal_search(chrom,dis_matrix,tabu_list, cnum, d, c, p)
        if new_value < best_value:#优于最优解
            best_value,best_chrom = new_value,new_chrom#更新最优解
            best_value_list.append(best_value)
        print('第%.d代最优值 %.1f' % (itera,best_value))
        chrom,value = new_chrom,new_value#更新当前解
        
        #更新禁忌表
        tabu_time = [x-1 for x in tabu_time]
        if 0 in tabu_time:
            tabu_list.remove(tabu_list[tabu_time.index(0)])
            tabu_time.remove(0)
        
        tabu_list.append(chrom)
        tabu_time.append(tabu_limit)
        itera +=1
    #画图
    draw_path(best_chrom, demandCoordinates, centerCoordinates, p, cnum)

2.4.3 例子求解结果

###计算例子（随机）
#需求点位置及需求量，备选中心位置及能力
demandCoordinates = [(88, 16),(25, 76),(69, 13),(73, 56),(80, 100),(22, 92),(32, 84),(73, 46),(29, 10),(92, 32),(44, 44),(55, 26),(71, 27),(51, 91),(89, 54),(43, 28),(40, 78)]
centerCoordinates = [(32, 60),(69, 33),(49, 40),(72, 81),(61, 65)]
d = [3,4,5,6,7,4,2,3,4,5,6,3,5,4,3,5,1]#需求量，对应demandCoordinates
c = [25,25,25,25,25]#能力都设置为25，对应centerCoordinates

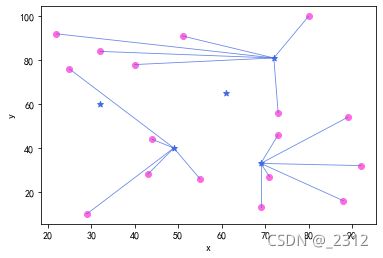
计算结果（*表示备选物流中心，圆点表示需求点）

选址问题目录

场景	算法求解
p-中心	带容量约束的p-中心选址问题建模与求解
覆盖问题	最大覆盖选址问题建模与求解