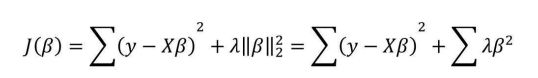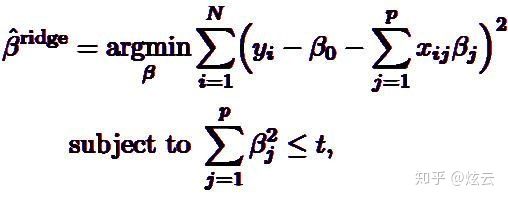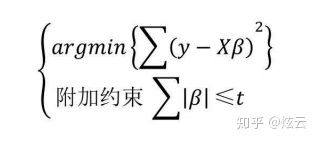python 回归_岭回归与LASSO回归 Ridge 和 Lasso Regression（python）

概述

• Ridge 和 Lasso回归是正则化技术的两种类型
• 正则化技术用于处理过度拟合和数据集过大的情况
• Ridge 和 Lasso回归涉及增加罚款的回归函数

炫云：你应该知道7个回归技巧!

炫云：线性回归算法的评估指标

炫云：Regression炫云：逻辑回归炫云：logistic Regression炫云：逻辑斯蒂回归模型

炫云：Ridge 和 Lasso Regression（python）

介绍

当我们讨论回归时，我们经常以讨论线性回归和逻辑回归结束。但是，这还不是结束。你知道有7种回归吗?

线性回归和逻辑回归是回归家族中最受欢迎的成员。上周，我在纽约数据科学学院(NYC Data Science Academy)观看了DataRobot首席产品官欧文·张(Owen Zhang)的一段录音讲话。他说:“如果你使用没有正规化的回归，你必须非常特别!”我希望你能明白他这种人指的是什么。

我很好地理解了它，并决定详细地探索正则化技术。

在这篇文章中，我解释了“Ridge Regression”和“Lasso Regression”背后的复杂科学，这是数据科学中使用的最基本的正则化技术，遗憾的是仍然没有被很多人使用。

回归的总体思想是一样的。决定模型系数的方式决定了所有的不同。我强烈建议你在阅读这篇文章之前先进行多元回归分析。您可以从这篇文章或任何其他首选的资料中获得帮助。

目录

1. 简要概述——“Ridge Regression”和“Lasso Regression”有什么不同?
2. 为什么要惩罚系数的大小-为什么它们应该起作用?
3. Ridge Regression——如何工作?
4. Lasso Regression——如何工作?
5. 潜入数学(可选)——一些基本的数学原理。
6. 结论——“Ridge Regression”和“Lasso Regression”的比较

1. Brief Overview

“Ridge Regression”和“Lasso Regression”是强大的技术，通常用于创建存在“大量”特征的简约模型。这里的“大”一般指两种情况:

1. 大到足以增强模型过度拟合的趋势(超过10个变量可能导致过度拟合)
2. 大到足以引起计算上的挑战。对于现代系统，这种情况可能出现在数百万或数十亿个特征的情况下

虽然Ridge和Lasso看起来是为了一个共同的目标而工作，但是它们的固有特性和实际用例有很大的不同。如果你以前听说过它们，你一定知道它们通过惩罚特征系数的大小以及最小化预测和实际观测之间的误差来工作。这些被称为“正规化”技术。关键的区别在于他们如何分配惩罚系数:

1. Ridge Regression:

• 执行L2正则化，即增加相当于系数大小的平方的惩罚
• 最小化目标= LS Obj +α*(系数的平方之和)

2.Lasso Regression:

• 执行L1正则化，即对系数的绝对值进行惩罚
• 最小化目标= LS Obj +α*(系数的绝对值的总和)

注意这里的“LS Obj”指的是“最小二乘目标”，即没有正则化的线性回归目标。

如果像“惩罚”和“正则化”这样的术语对您来说非常陌生，不要担心，我们将在本文中更详细地讨论这些术语。在深入研究它们是如何工作的之前，让我们先试着对为什么惩罚系数的大小应该在一开始就起作用有一些直觉。

2. 为什么要惩罚系数的大小？

让我们试着理解模型复杂性对系数大小的影响。例如，我模拟了一个正弦曲线(在60°到300°之间)，并使用如下代码添加了一些随机噪声:

#Importing libraries. The same will be used throughout the article.
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 10

#Define input array with angles from 60deg to 300deg converted to radians
x = np.array([i*np.pi/180 for i in range(60,300,4)])
np.random.seed(10)  #Setting seed for reproducibility
y = np.sin(x) + np.random.normal(0,0.15,len(x))
data = pd.DataFrame(np.column_stack([x,y]),columns=['x','y'])
plt.plot(data['x'],data['y'],'.')

这类似于正弦曲线，但并不完全是因为噪音。在本文中，我们将使用这个示例来测试不同的场景。我们试着用多项式回归来估计正弦函数，幂函数是x从1到15。让我们在dataframe中为每个power到15添加一列。这可以通过以下代码来实现:

for i in range(2,16):  #power of 1 is already there
    colname = 'x_%d'%i      #new var will be x_power
    data[colname] = data['x']**i
print(data.head())

现在我们有了所有的15次幂，让我们建立15个不同的线性回归模型每个模型包含从1到特定型号的x次幂的变量。例如，模型8的特征集将是- {

}。

首先，我们将定义一个泛型函数，该函数接受所需的x的最大功率作为输入，并返回一个包含- [model RSS、intercept、coef_x、coef_x2，…upto entered power]的列表。这里，RSS指的是“残差平方和”，也就是训练数据集中预测值与实际值误差平方和。定义该函数的python代码为:

#Import Linear Regression model from scikit-learn.
from sklearn.linear_model import LinearRegression
def linear_regression(data, power, models_to_plot):
    #initialize predictors:
    predictors=['x']
    if power>=2:
        predictors.extend(['x_%d'%i for i in range(2,power+1)])
    
    #Fit the model
    linreg = LinearRegression(normalize=True)
    linreg.fit(data[predictors],data['y'])
    y_pred = linreg.predict(data[predictors])
    
    #Check if a plot is to be made for the entered power
    if power in models_to_plot:
        plt.subplot(models_to_plot[power])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for power: %d'%power)
    
    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([linreg.intercept_])
    ret.extend(linreg.coef_)
    return ret

注意，这个函数不会绘制适合所有幂次的模型，而是返回所有模型的RSS和系数。为了保持简洁，我将暂时跳过代码的细节。

现在，我们可以制作所有15个模型并比较结果。为了便于分析，我们将所有结果存储在一个panda dataframe中，并绘制6个模型来了解趋势。考虑以下代码:

#Initialize a dataframe to store the results:
col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['model_pow_%d'%i for i in range(1,16)]
coef_matrix_simple = pd.DataFrame(index=ind, columns=col)

#Define the powers for which a plot is required:
models_to_plot = {1:231,3:232,6:233,9:234,12:235,15:236}

#Iterate through all powers and assimilate results
for i in range(1,16):
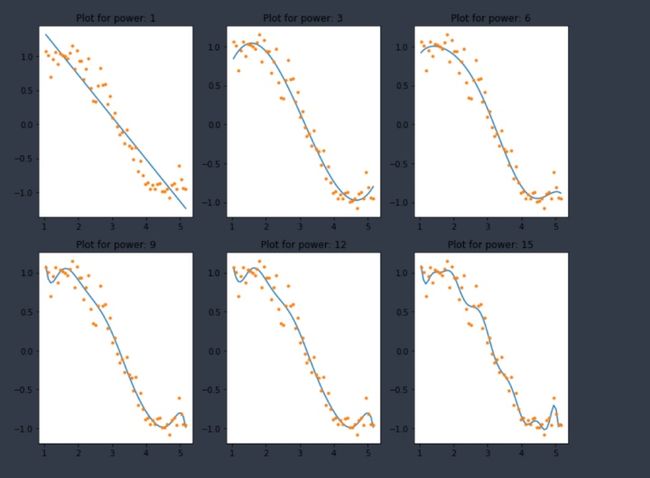
    coef_matrix_simple.iloc[i-1,0:i+2] = linear_regression(data, power=i, models_to_plot=models_to_plot)

我们期望越来越复杂的模型能够更好地适应数据，从而降低RSS值。这可以通过查看6个模型生成的图来验证:

这显然符合我们最初的理解。随着模型复杂度的增加，模型对训练数据集的拟合偏差会越来越小。虽然这会导致过度拟合，但我们先把这个问题放一段时间，回到我们的主要目标上，即对系数大小的影响。这可以通过查看上面创建的数据框架进行分析。

Python Code:

#Set the display format to be scientific for ease of analysis
pd.options.display.float_format = '{:,.2g}'.format
coef_matrix_simple

很明显，随着模型复杂度的增加，系数的大小呈指数增长。我希望这能给我们一些直观的认识，为什么对系数的大小施加限制是一个减少模型复杂性的好主意。

让我们试着更好地理解这一点。

大系数表示什么?这意味着我们非常强调那个特征，也就是说，特定的特征是一个很好的预测结果的指标。当它变得太大时，该算法开始建立复杂的关系模型来估计输出，并最终过度拟合特定的训练数据。

我希望概念是清楚的。如果需要，我很乐意在评论中进一步讨论。现在，让我们详细了解“Ridge Regression”和“Lasso Regression”，看看他们如何工作的相同的问题。

3. Ridge Regression

如前所述，岭回归进行了“L2正则化”，即在优化目标中加入系数平方和因子。因此，岭回归优化如下:

Objective = RSS + α * (sum of square of coefficients)

这里,α (alpha)的参数有平衡对最小化RSS的强调 和系数平方之和最小化的作用。α可以采取不同的值:

1. α = 0:

• The objective becomes same as simple linear regression.
• We’ll get the same coefficients as simple linear regression.

2.α = ∞:

• • The coefficients will be zero. Why? Because of infinite weightage on square of coefficients, anything less than zero will make the objective infinite.

3.0 < α < ∞:

• • The magnitude of α will decide the weightage given to different parts of objective.
  • The coefficients will be somewhere between 0 and ones for simple linear regression.

我希望这给某种意义上α如何影响系数的大小。有一件事是肯定的，任何非零值将给出的值小于简单线性回归。由多少?我们很快就会知道了。把数学细节留到以后，让我们看看岭回归在同一问题上的作用。

首先，让我们定义一个与简单线性回归相似的Ridge Regression通用函数。Python代码是:

from sklearn.linear_model import Ridge
def ridge_regression(data, predictors, alpha, models_to_plot={}):
    #Fit the model
    ridgereg = Ridge(alpha=alpha,normalize=True)
    ridgereg.fit(data[predictors],data['y'])
    y_pred = ridgereg.predict(data[predictors])
    
    #Check if a plot is to be made for the entered alpha
    if alpha in models_to_plot:
        plt.subplot(models_to_plot[alpha])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for alpha: %.3g'%alpha)
    
    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([ridgereg.intercept_])
    ret.extend(ridgereg.coef_)
    return ret

注意这里使用的“Ridge”函数。它在初始化时接受' alpha '作为参数。此外，请记住，在每种类型的回归中，对输入进行归一化通常是一个好主意，在Ridge Regression中也应该使用。

现在,对10个不同值的α值从1e-15 to 20的Ridge Regression进行分析。这些值被选择,这样我们可以很容易地分析与α的值变化趋势。然而，这些情况因情况而异。

注意，这10个模型中的每一个都包含所有15个变量，只有alpha值不同。这与简单线性回归的情况不同，在简单线性回归中，每个模型都有一个特征子集。

#Initialize predictors to be set of 15 powers of x
predictors=['x']
predictors.extend(['x_%d'%i for i in range(2,16)])

#Set the different values of alpha to be tested
alpha_ridge = [1e-15, 1e-10, 1e-8, 1e-4, 1e-3,1e-2, 1, 5, 10, 20]

#Initialize the dataframe for storing coefficients.
col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['alpha_%.2g'%alpha_ridge[i] for i in range(0,10)]
coef_matrix_ridge = pd.DataFrame(index=ind, columns=col)

models_to_plot = {1e-15:231, 1e-10:232, 1e-4:233, 1e-3:234, 1e-2:235, 5:236}
for i in range(10):
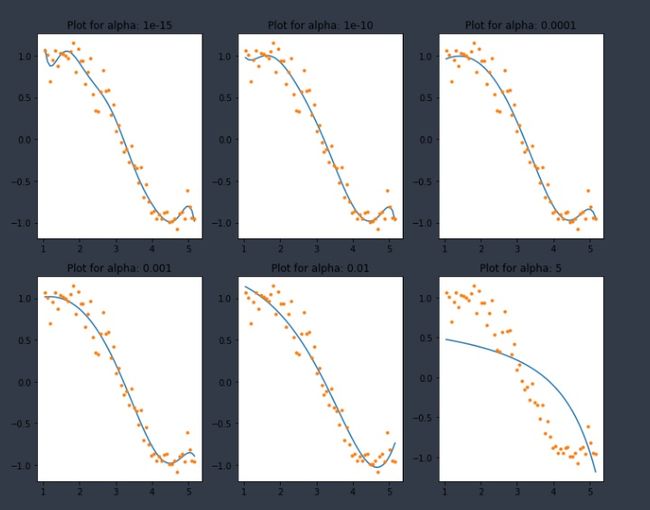
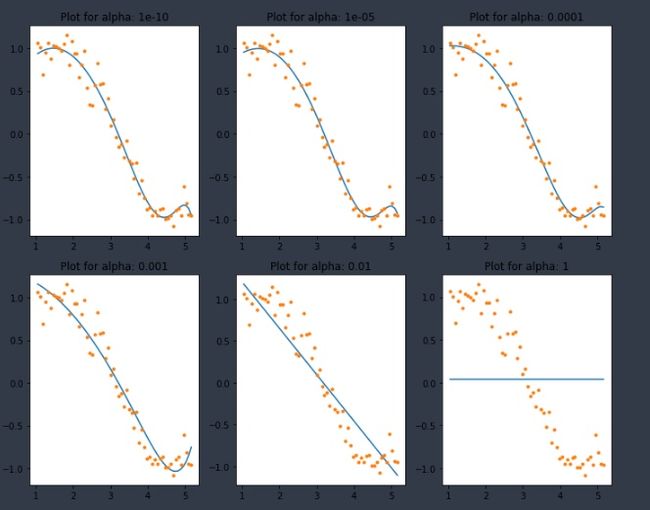
    coef_matrix_ridge.iloc[i,] = ridge_regression(data, predictors, alpha_ridge[i], models_to_plot)

在这里我们可以清楚地观察到，随着alpha值的增加，模型的复杂度降低。虽然较高的alpha值可以减少过拟合，但显著较高的alpha值也会导致欠拟合(例如alpha = 5)。因此，应该明智地选择。一种被广泛接受的技术是交叉验证，即alpha值在一个值范围内迭代，并选择一个给出较高交叉验证分数的值。

让我们看看上述模型中系数的值:

#Set the display format to be scientific for ease of analysis
pd.options.display.float_format = '{:,.2g}'.format
coef_matrix_ridge

这直接给了我们以下推论:

1. RSS随着alpha值的增加而增加，这个模型的复杂度降低了
2. 小到1e-15的alpha值使系数的大小显著减小。如何?比较该表第一行的系数与简单线性回归表的最后一行的系数。
3. 高alpha值会导致显著的拟合不足。注意，当alpha值大于1时，RSS的增长很快
4. 虽然这些系数非常非常小，但它们不是零。

前三个非常直观。但第四点也是很重要的一点。让我们通过确定系数数据集中每行的0的个数来再次确认:

coef_matrix_ridge.apply(lambda x: sum(x.values==0),axis=1)

这证实了所有15个系数在大小上都大于零(可以是+ve或-ve)。记住这个观察结果，再看一遍，直到看清楚为止。这将在以后的ridge与lasso regression的比较中起到重要的作用。

4. Lasso Regression

LASSO代表最小绝对收缩和选择操作符。我知道它没有给出太多的概念，但这里有两个关键词——“绝对”和“选择”。

让我们先考虑前者，然后再考虑后者。

Lasso回归进行L1正则化，即在优化目标中加入系数绝对值之和的因子。因此，lasso回归优化了以下方面:

Objective = RSS + α * (sum of absolute value of coefficients)

在这里,α (alpha)类似于ridge提供了一个平衡RSS和系数的大小之间的作用。这样,α可以取不同的值。让我们在这里简单地重复一下:

1. α = 0: Same coefficients as simple linear regression
2. α = ∞: All coefficients zero (same logic as before)
3. 0 < α < ∞: coefficients between 0 and that of simple linear regression

是的，直到现在它看起来和Ridge很像。不过，你等一下，等我们讲完的时候，你就会知道区别了。像以前一样，让我们运行lasso regression对相同的问题如上。首先，我们将定义一个泛型函数:

from sklearn.linear_model import Lasso
def lasso_regression(data, predictors, alpha, models_to_plot={}):
    #Fit the model
    lassoreg = Lasso(alpha=alpha,normalize=True, max_iter=1e5)
    lassoreg.fit(data[predictors],data['y'])
    y_pred = lassoreg.predict(data[predictors])
    
    #Check if a plot is to be made for the entered alpha
    if alpha in models_to_plot:
        plt.subplot(models_to_plot[alpha])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for alpha: %.3g'%alpha)
    
    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([lassoreg.intercept_])
    ret.extend(lassoreg.coef_)
    return ret

注意在Lasso函数中定义的附加参数‘max_iter’。这是我们希望模型运行的最大迭代次数，如果它之前没有收敛的话。这对于Ridge也是存在的，但是在本例中需要将其设置为高于默认值。为什么?我将在下一节讨论这个问题，把它放在信封的后面。

让我们检查输出的10个不同的值的alpha使用以下代码:

#Initialize predictors to all 15 powers of x
predictors=['x']
predictors.extend(['x_%d'%i for i in range(2,16)])

#Define the alpha values to test
alpha_lasso = [1e-15, 1e-10, 1e-8, 1e-5,1e-4, 1e-3,1e-2, 1, 5, 10]

#Initialize the dataframe to store coefficients
col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['alpha_%.2g'%alpha_lasso[i] for i in range(0,10)]
coef_matrix_lasso = pd.DataFrame(index=ind, columns=col)

#Define the models to plot
models_to_plot = {1e-10:231, 1e-5:232,1e-4:233, 1e-3:234, 1e-2:235, 1:236}

#Iterate over the 10 alpha values:
for i in range(10):
    coef_matrix_lasso.iloc[i,] = lasso_regression(data, predictors, alpha_lasso[i], models_to_plot)

这再次告诉我们，模型的复杂性随着alpha值的增加而降低。注意到=1处的直线。我觉得有点奇怪。让我们进一步探讨这个问题，通过查看系数:

除了对更高的alphas有更高的RSS的预期推断，我们还可以看到以下几点:

1. 对于相同的alpha值，lasso回归的系数要比ridge回归的小得多(比较两个表的第一行)。
2. 对于相同的alpha值，与ridge回归相比，lasso具有更高的相对过饱和度(较差的拟合)
3. 很多系数是零，即使是很小的值

推论#1、2可能不总是泛化，但在很多情况下都适用。与ridge回归的真正区别在于最后的推理。我们使用以下代码检查每个模型中系数为0的数量:

coef_matrix_lasso.apply(lambda x: sum(x.values==0),axis=1)

我们可以观察到，即使是很小的值，大量的系数都是零。这也解释了在lasso中alpha=1的水平线，它只是一个基线模型!这种系数大部分为零的现象称为“稀疏性”。虽然lasso执行特性选择，但这种程度的稀疏性只在特殊情况下才能实现，我们将在最后讨论这种情况。

这对lasso回归和ridge回归的用例有一些非常有趣的影响。但是在进行最后的比较之前，让我们来鸟瞰一下为什么在lasso回归情况下系数是零而不是ridge回归背后的数学原理。

5. Sneak Peak into Statistics (Optional)

我个人喜欢统计学，但你们很多人可能不喜欢。这就是为什么我特别把这个部分标记为“可选”。如果你觉得你可以处理这些算法，而不需要研究它们背后的数学原理，我完全尊重你的决定，你可以随意跳过这一部分。

但我个人认为，从长远来看，对事情的运作方式有一些基本的了解是有帮助的。

我答应过的，我会把它放在鸟瞰的地方。如果你想深入了解细节，我建议你买一本好的统计学教科书。我最喜欢的是统计学习的要素之一。最棒的是，作者们已经将它免费提供了。

让我们从回顾回归问题中数据的基本结构开始。

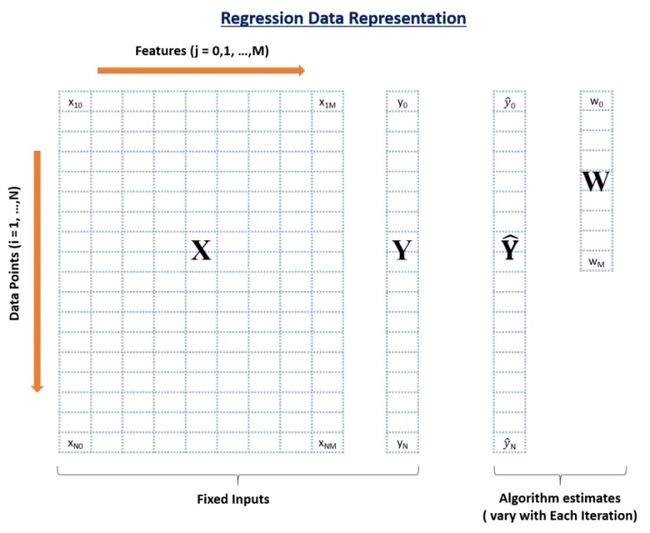
在这张信息图中，你可以看到有4个数据元素:

1. X: 输入特征矩阵 (nrow: N, ncol: M+1)
2. Y: 实际结果值 (length:N)
3. Yhat: 这些是Y的预测值 (length:N)
4. W: 权重或系数 (length: M+1)

这里，N是可用数据点的总数，M是特征的总数。X有M+1列因为有M个特征和1个截距

任意数据点i的预测结果为:

它只是以系数为权重的每个数据点的加权和。这种预测是通过根据一定的标准找到最优的权值来实现的，而权值取决于所使用的回归算法的类型。让我们考虑所有3种情况:

1. Simple Linear Regression

要最小化的目标函数(也称为成本)就是RSS(残差平方和)，即预测结果与实际结果的平方误差之和。这可以用数学描述为:

为了使成本最小化，我们通常使用“梯度下降”算法。我现在不会讲细节，但是你可以参考这个。整体算法如下:

1. 初始化权值(比如w=0)

2. 迭代直到不收敛

• 2.1遍历所有特性(j=0,1…M)
• ......2.1.1确定梯度
• ......2.1.2更新第j个权值，用学习率减去梯度
• .......w(t+1) = w(t) -学习率*梯度

这里重要的一步是#2.1.1，在这里我们计算梯度。梯度只不过是cost(w)相对于某一特定权重(记作wj)的偏微分。第j个权值的梯度为:

它由两部分组成:

1. 2*{..} : 这是因为我们在{..}中对该项的平方进行了微分。
2. -wj : 这是对{..}关于wj微分。虽然它是一个和，但其他的都是0，只有wj会保留。

步骤#2.1.2涉及到使用梯度更新权重。简单线性回归的更新步骤如下:

我希望你能跟上。注意，RHS中的+ve符号是由两个-ve符号相乘而成的。我想解释一下上面提到的梯度下降算法的第2点“迭代直到不收敛”。这里的收敛是指在预先定义的极限内获得最优解。

它是使用梯度值来检查的。如果梯度足够小，这意味着我们非常接近最优，进一步的迭代不会对系数产生实质性的影响。可以使用“tol”参数更改梯度的下限。

现在我们来考虑一下ridge regression的情况

2. Ridge Regression

要最小化的目标函数(也称为代价函数)是RSS加上权值大小的平方和。这可以用数学描述为:

在这种情况下，梯度应该是:

同样在梯度的正则化部分，只剩下wj，其余都为零。对应的更新规则为:

这里我们可以看到，RHS的第二部分和简单线性回归是一样的。因此,岭回归相当于减少权重的因素(1-2λη),然后应用相同的更新规则简单线性回归。我希望这能给你们一些直观的理解为什么这些系数会减小到很小的数但不会变成0。

注意，在这种情况下，收敛的标准与简单的线性回归类似，即检查梯度的值。

目标函数J(β)最小化问题等价于下方的式子：

以两个变量为例，解释岭回归的几何意义:

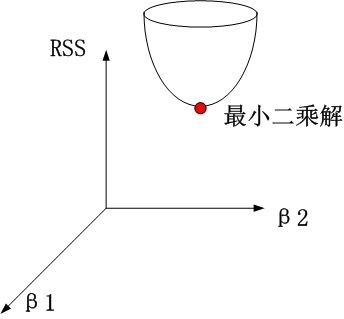
1、没有约束项时

系数β1和β2已经经过标准化。残差平方和RSS可以表示为β1和β2的一个二次函数，数学上可以用一个抛物面表示。

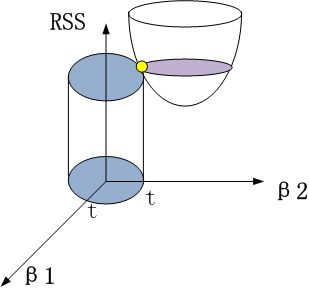
2、岭回归时

约束项为

，对应着投影为β1和β2平面上的一个圆，即下图中的圆柱。

该圆柱与抛物面的交点对应的β1、β2值，即为满足约束项条件下的能取得的最小的β1和β2.

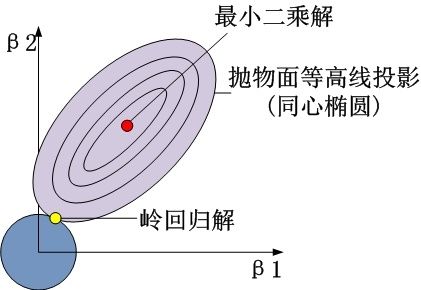
从β1β2平面理解，即为抛物面等高线在水平面的投影和圆的交点，如下图所示

可见岭回归解与原先的最小二乘解是有一定距离的。

岭回归性质：

1）当岭参数为0，得到最小二乘解。

2）当岭参数λ趋向更大时，岭回归系数β估计趋向于0。

3）岭回归中的

是回归参数β的有偏估计。它的结果是使得残差平和变大，但是会使系数检验变好，即R语言summary结果中变量后的*变多。

4）在认为岭参数λ是与y无关的常数时，是最小二乘估计的一个线性变换，也是y的线性函数。 但在实际应用中，由于λ总是要通过数据确定，因此λ也依赖于y、因此从本质上说，并非的线性变换，也非y的线性函数。

5）对于回归系数向量来说，有偏估计回归系数向量长度<无偏估计回归系数向量长度，

，即比理想值要短。

6）存在某一个λ，使得它所对应的的MSE（估计向量的均方误差）<最小二乘法对应估计向量的的MSE。

即 存在λ>0，使得

理解 ： 和β平均值有偏差，但不能排除局部可以找到一个比更接近β。

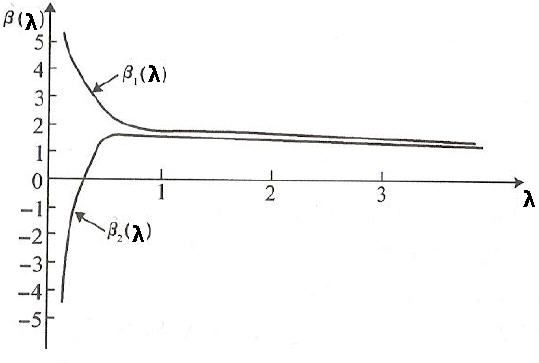
岭迹图：

1）观察λ较佳取值；

2）观察变量是否有多重共线性；

可见，在λ很小时，通常各β系数取值较大；而如果λ=0，则跟普通意义的多元线性回归的最小二乘解完全一样；当λ略有增大，则各β系数取值迅速减小，即从不稳定趋于稳定。 上图类似喇叭形状的岭迹图，一般都存在多重共线性。

λ的选择：一般通过观察，选取喇叭口附近的值，此时各β值已趋于稳定，但总的RSS又不是很大。

选择变量：删除那些β取值一直趋于0的变量。

3. Lasso Regression

要最小化的目标函数(也称为代价函数)是RSS加上权值绝对值的和。这可以用数学描述为:

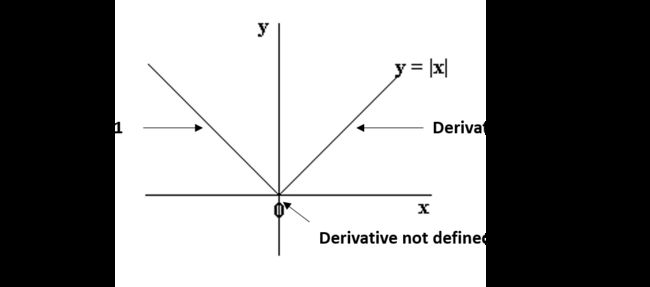
在这种情况下，梯度不被定义为在x=0处绝对函数不可微。这可以说明如下:

我们可以看到，0左右两边的部分是直线，有定义的导数，但是在x=0处不能微分。在这种情况下，我们必须使用一种不同的技术，称为坐标下降，这是基于梯度下降的概念。其中一个坐标下降遵循以下算法(这也是sklearn的默认算法):

1. initialize weights (say w=0)
2. iterate till not converged
   2.1 iterate over all features (j=0,1...M)
       2.1.1 update the jth weight with a value which minimizes the cost

#2.1.1可能看起来太一般化了。但我有意留下细节，跳到更新规则:

这里g(w-j)表示(但不完全)实际结果与预测结果之间的差异，除了第j个变量。如果这个值很小，这意味着即使没有第j个变量，该算法也能够很好地预测结果，因此可以通过设置零系数将其从方程中删除。这给了我们一些直觉，为什么在lasso回归的情况下，系数变成了零。

在坐标下降法中，检查收敛性是另一个问题。由于梯度没有定义，我们需要一个替代方法。存在许多替代方法，但最简单的一种是检查算法的步长。我们可以在任何特定的循环中检查所有特性权重的最大差异(以上algo中的#2.1)。

如果这个值小于指定的“tol”，则algo将停止。收敛速度不如梯度下降快，如果出现一个警告说算法在收敛前停止，我们可能不得不设置' max_iter '参数。这就是我在Lasso泛型函数中指定此参数的原因。

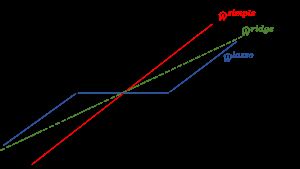
让我们总结一下我们的理解，通过比较所有三种情况下的系数，使用下面的视觉，它显示了和ridge、lasso系数相比，简单的线性回归情况。

为缺乏视觉吸引力而道歉。但我认为，重新灌输以下事实就足够了:

1. ridge的系数是简单线性回归系数的一个简化因子，因此不会达到零值，而是很小的值
2. lasso的系数在一定范围内变为零，并被一个常数因子降低，这就解释了lasso系数相对于ridge来说较低的幅度。

在深入之前，一个重要的问题，在ridge和lasso regression是拦截处理。一般来说，将截距正规化不是一个好主意，应该将其排除在正规化之外。这需要在实现中进行一些细微的更改，我将留给您来研究。

将LASSO回归的目标函数写成下方的式子：

几何意义:

将LASSO回归模型目标函数J(β)的最小化 问题等价转换为下方的式子:

这里仅以两个自变量的回归模型为例，将目标函数中的两个部分表示为 :

将LASSO回 归的惩罚项映射到二维空间的话，就会形成“角”，一旦“角”与抛物面相 交，就会导致β1为0，进而实现变量的删除。而且相比于圆面，

正则项的方框顶点更容易与抛物面相交，起到变量筛选的效果。

所以，LASSO回归不仅可以实现变量系数的缩减（如二维图中，抛 物面的最小二乘解由黑点转移到了相交的红点，β2系数明显被“压 缩”了），而且还可以完成变量的筛选，对于无法影响因变量的自变 量，LASSO回归都将其过滤掉。

现在，让我们来结束的部分，我们比较ridge和lasso regression技术，看看这些可以使用。

6. Conclusion

既然我们已经对ridge和lasso回归的工作原理有了一个大致的了解，让我们通过比较它们来巩固我们的理解，并尝试理解它们的具体用例。我还将把它们与一些替代方法进行比较。让我们来分析一下以下三个方面:

1. Key Difference

• Ridge: 它包含模型中的所有(或不包含)特性。因此，岭回归的主要优点是系数收缩和降低模型的复杂性。
• Lasso: 除了收缩系数之外，Lasso还执行特征选择。(还记得Lasso在前文中的“选择”吗?)正如我们前面所观察到的，一些系数正好为零，这就相当于将特定的特征排除在模型之外。

传统上，采用逐步回归等技术来进行特征选择和简化模型。但是随着机器学习的进步，ridge和lasso回归提供了很好的替代方法，因为它们提供了更好的输出，需要更少的调优参数，并且可以在很大程度上实现自动化。

2. Typical Use Cases

• Ridge: 主要用于防止过度拟合。因为它包含了所有的特性，所以在#特性过高的情况下，比如以百万计，它不是很有用，因为它会带来计算上的挑战。
• Lasso: 因为它提供了稀疏的解决方案，所以它通常是建模用例的选择模型(或者这个概念的一些变体)，在这些用例中#特性有数百万甚至更多。在这种情况下，获得一个稀疏解具有很大的计算优势，因为零系数的特征可以简单地忽略。

3. Presence of Highly Correlated Features

• Ridge: 即使存在高度相关的特征，它通常也能工作得很好，因为它会把所有的特征都包含在模型中，但是系数会根据相关性分布在各个特征之间。
• Lasso: 在高度相关的特征中任意选择一个特征，将其余特征的系数降为0。此外，所选择的变量随模型参数的变化而随机变化。与Ridge回归相比，这种方法通常效果不佳。

我们在上面讨论的例子中可以看到lasso的这个缺点。由于我们使用的是多项式回归，所以变量之间高度相关。(不知道为什么?检查data.corr()）的输出。因此，我们看到即使是很小的alpha值也会给出显著的稀疏性(即高的#系数为零)。

End Notes

在本文中，我概述了使用ridge和lasso回归的正则化。然后，我集中讨论了惩罚系数大小背后的原因，这将给我们提供一个简洁的模型。接下来，我们详细讨论了ridge和lasso回归，并看到了它们相对于简单线性回归的优势。我们对它们为什么会起作用以及如何起作用有了一些直觉。如果你读了可选的数学部分，你可能就理解了基本原理。

正则化技术非常有用，我鼓励您实现它们。如果你已经准备好接受挑战，为什么不试试。

你觉得这篇文章有用吗?对你来说太复杂了还是只是在公园里散步?你有什么需要我改进的吗?请分享您宝贵的反馈，帮助我以后更好地对待您。