《Think Python 2e》作业实现（四）： 案例研究—接口设计
《Think Python 2e》作业实现（四）： 案例研究—接口设计
文章目录
- 《Think Python 2e》作业实现（四）： 案例研究—接口设计
- 这是什么？
- 习题4-1：画函数堆栈图
- 习题4-2：用函数绘制花朵
- 习题4-3：用函数绘制饼图
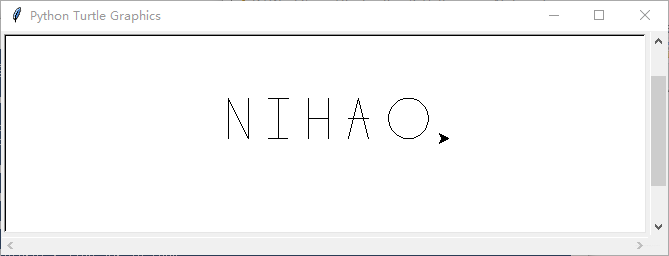
- 习题4-4：用函数绘制字母
- 习题4-5：用函数绘制螺线
这是什么？
这里是《Think Python 2e》作业实现 ！在这里将记录《Think Python 2e》作业的练习记录、终端信息和结果分析。
- 这是《Think Python 2e》哪个版本的作业？
《Think Python：如何像计算机科学家一样思考》第二版。这里主要参考了一个中文网页版《Think Python 2e》中译本。- 可以当成《Think Python 2e》参考答案吗？
这里主要记录了我自己完成作业时所产生的成果及习题总结，基本未参考教材所提供的答案，未免有失规范，参考答案建议还是以 绿茶出版社官方代码 为准。- 不同的解释器版本结果不尽相同，这里用的哪个版本Python解释器？
这里用了Python 3.8.6版解释器，部分用安卓Pydroid 4.01_arm64中的3.8.3版Python解释器，在线解释器用教程推荐的PythonAnywhere中的3.8版Python解释器。
习题4-1：画函数堆栈图
【习题4.1.1】 画函数 circle 重构后的堆栈图
import math
import turtle
bob = turtle.Turtle()
def polygon_arc(t, length, n, angle):
m = int(n * angle / 360)
for i in range(m):
t.fd(length)
t.lt(360 / n)
def arc(t, r, angle):
circumference = 2 * math.pi * r
n = int(circumference / 3) + 1
length = circumference / n
polygon_arc(t, length, n , angle)
def circle(t, r):
arc(t, r, 360)
circle(bob, 100)
turtle.mainloop()
- 练习记录：
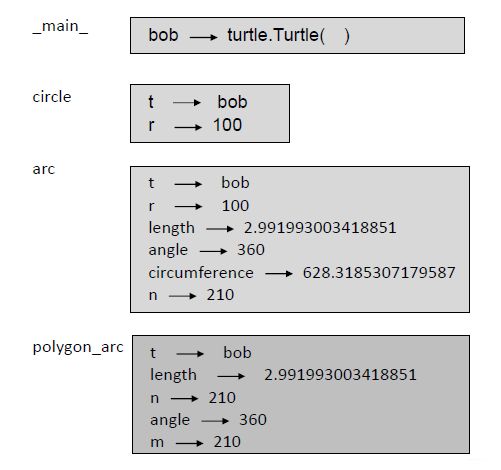
- 结果分析：
- 每个函数用一个栈帧（frame）表示，每个栈帧一个线框
- 函数名写在线框外，例如本题中的函数名 arc
- 形参及函数内部变量写在线框内：
- 形参及其指向实参值，例如函数 arc 的形参 t、 r 和 angle 及其指向实参值
- 函数内部变量及其指向值，例如函数 arc 内部变量 n、length 和 circumference 及其指向值
【习题4.1.2】 让画的圆左偏转一个角度以使其（位置）更精确
- 练习记录：
import math
import turtle
bob = turtle.Turtle()
tom = turtle.Turtle()
jack = turtle.Turtle()
def polygon_arc(t,length,n,angle):
m = int(n*angle/360)
for i in range(m):
t.fd(length)
t.lt(360/n)
def arc(t, r, angle):
circumference = 2 * math.pi * r
n = int(circumference / 30) + 1
length = circumference / n
polygon_arc(t, length,n, angle)
def arc_left(t, r, angle):
circumference = 2 * math.pi * r
n = int(circumference / 30) + 1
length = circumference / n
t.lt(angle/n/2) # 左偏画笔每笔偏转角一半，如教程答案代码所示
polygon_arc(t, length,n, angle)
t.rt(angle/n/2) # 右偏画笔每笔偏转角一半，消除画笔左偏引起的改变
def arc_circle(t, r, angle):
circumference = 2 * math.pi * r
n = int(circumference) + 1 # 以近似每像素画一笔的精度，画出更精细的圆形线性近似即标准圆
length = circumference / n
polygon_arc(t, length,n, angle)
def circle(t, r):
arc(t, r, 360)
def circle_left(t, r):
arc_left(t, r, 360)
def circle_circle(t, r):
arc_circle(t, r, 360)
bob.pencolor(0,0,1)
circle(bob, 100)
tom.pencolor(1,0,0)
circle_left(tom, 100)
jack.pencolor(0,1,0)
circle_circle(jack, 100)
#turtle.circle(100)
turtle.mainloop()
- 结果分析：
- 所谓标准圆，实为更精细的圆形线性近似（linear approximation），也可以调用 turtle.circle() 函数画标准圆
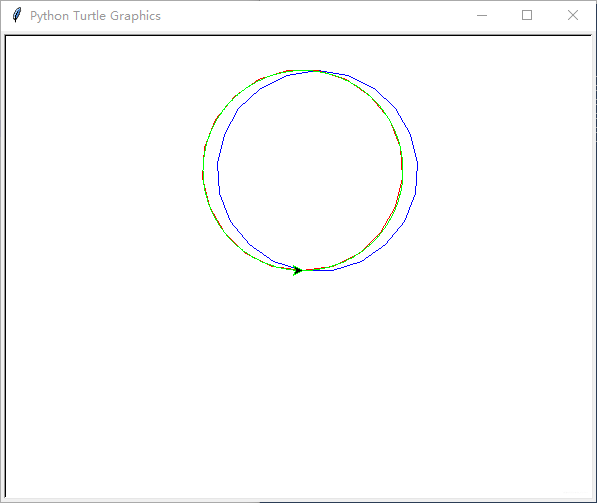
- 画三个圆即标准圆、画笔未提前偏转的圆及画笔提前左偏转一定角度的圆以做对比，以体现画笔提前左偏转一定角度后的效果；为便于对比，画不同的圆用不同颜色的画笔，为此找到了 Turtle 对象的方法 pencolor() ，通过
bob.pencolor(0,0,1)语句使用蓝色画笔，通过tom.pencolor(1,0,0)语句使用红色画笔，通过jack.pencolor(0,1,0)语句使用绿色画笔 - 从所画三个圆可见，调用函数 circle 所画的圆形线性近似（蓝色圆）在标准圆（绿色圆）的右侧、比标准圆右偏了一个角度
- 调用重构（使画笔提前左偏画圆时每笔所须偏转的角度的一半）后的函数 circle_left 所画的圆形线性近似（红色圆）与标准圆基本重合，说明画笔提前左偏转一定角度所画的圆整体向左偏转了一定的角度，确实如题所说（位置）更精确
- 从这个题可见，函数 circle 所使用的方法有误差，改用直接计算小乌龟所画的弦线的长度经检验更准确，就不会有位置偏差；方法、算法其实比计算机本身计算的精确度、算力更重要，对结果影响更大
习题4-2：用函数绘制花朵
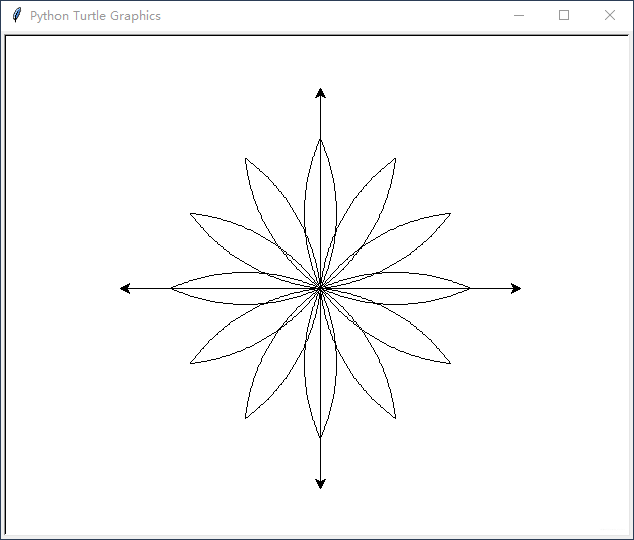
【习题】 编写比较通用的一个可以画出像教材图4-1中那样花朵的函数集
- 练习记录：
import math
import turtle
bob = turtle.Turtle()
tom = turtle.Turtle() # 为察看花瓣位置，创建 tom 等其他小乌龟以画坐标线
jack = turtle.Turtle()
sam = turtle.Turtle()
john = turtle.Turtle()
def flower(t, L, radio, n):
"""
用 Turtle 对象的 rt() 方法使画笔先右偏一个角度，使得第一个花瓣水平放置；
右偏的角度根据推算为花瓣边缘弧线所对圆心角（常规设为 2a ）的一半，即 a ；
L 为弦长，radio 为花瓣边缘弧线曲率（弧长与弦长的比值），n 为花瓣数
"""
t.rt(alfa(L, radio) / math.pi * 180)
for i in range(n):
petal(t, L, radio)
t.lt(360 / n)
def alfa(L, ratio):
"""
迭代法计算弧线所在圆的半径 r 并据此计算圆心角的一半即 a 的值，迭代法计算公式网上查得
"""
r = L / 2 # r 为圆半径，初值赋为 L/2（不得小于此值）
C = L * ratio # C 为弧线长度
for i in range(100000):
r = (1+(L-2*r*math.sin(C/(2*r)))/(L-C*math.cos(C/(2*r)))) * r
a = math.asin(( L / 2 ) / r) # a 为圆心角一半
return a # 取得函数 alfa 的返回值
def petal(t, L, ratio):
C = L * ratio
a = alfa(L, ratio)
arc(t, a, C)
t.lt(180 - (a * 2) / math.pi *180) # 小乌龟折返所偏转的角度根据几何知识计算而得，为180-2a
arc(t, a, C)
t.lt(180 - (a * 2) / math.pi *180) # 小乌龟偏转到画花瓣起始位置，偏转角度同样为 180-2a
def arc(t, a, C):
n = int(C / 2) + 1 # n 为画的笔数，约2个像素画一笔
step_arc = C / n
step_alfa = ((a * 2) / math.pi * 180) / n
t.lt(step_alfa / 2) # 如习题4-1-2答案代码所示，提前左偏半个每笔偏转角度以使位置更精确
for i in range(n):
t.fd(step_arc)
t.lt(step_alfa)
t.rt(step_alfa / 2)
jack.fd(200)
tom.lt(180)
tom.fd(200)
sam.lt(90)
sam.fd(200)
john.rt(90)
john.fd(200)
flower(bob, 150, 1.03, 12)
bob.ht() # 隐藏 bob ，使得花朵更唯美
turtle.mainloop()
- 结果分析：
- 实现了可通过输入不同实参设置花瓣数、花瓣长度和花瓣曲率（弧长与弦长比），比较通用
- 迭代法是计算机科学中的一个常用算法，这里的 a （圆心角一半）即用此法算得
- 函数返回值语句
return a用于定义函数 alfa 的返回值 - 使用了 Turtle 对象的方法 ht() ，以使小乌龟隐藏、花朵更唯美
- 切记圆心角角度 degree 与弧度 radian 的关系：
- degree = radian / math.pi * 180
- Turtle对象的 lt() 与 rt() 方法接受角度degree
- math模块中的函数如 math.sin 默认接受弧度 radian 实参
习题4-3：用函数绘制饼图
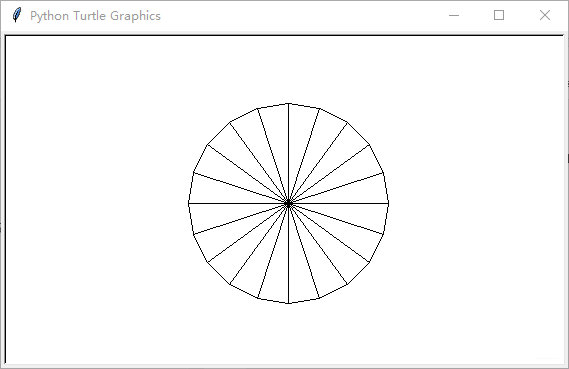
【习题】 编写比较通用的一个可以画出教材图4-2中那样图形的函数集
- 练习记录：
import math
import turtle
bob = turtle.Turtle()
def pie_chart(t, l, n):
for i in range(n): # 默认 i 从0开始计数,这影响下面两个语句的顺序
t.lt(360 / n * i)
component(t, l, n)
def component(t, l, n):
t.fd(l)
t.lt(180 - ((180 - 360 / n) / 2))
t.fd(2 * l * math.sin((360 / n) / 180 * math.pi / 2))
t.pu() # 提笔
t.home() # 如果此时笔处于放下状态，相当于从当时所处位置对准原点画到原点的线段并把笔转向初始方向
t.pd() # 放笔
pie_chart(bob, 100, 20)
bob.ht()
turtle.mainloop()
-
结果分析：
- 实现了可通过输入不同实参 l 设置饼图大小、输入实参 n 设置饼图分区数，比较通用
- Turtle 对象的home() 方法：使小乌龟转向原点、到原点画线段，并转向初始方向，除非笔处于抬起状态
for i in range():语句中的 i 默认从 0 开始计数
-
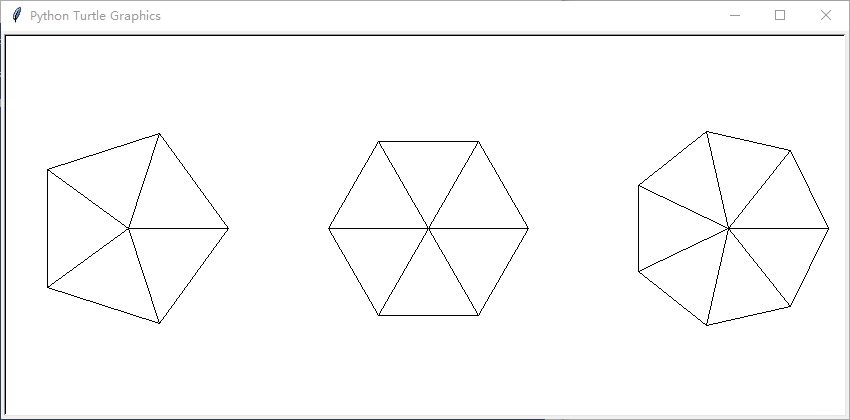
变形练习：（通过中心点移位，在不同位置画不同的饼图）
import math
import turtle
bob = turtle.Turtle()
def pie_chart(t, l, n):
for i in range(n):
t.lt(360 / n * i)
component(t, l, n)
def component(t, l, n):
x = t.xcor() # 获取小乌龟初始的 x 坐标
y = t.ycor() # 获取小乌龟初始的 y 坐标
t.fd(l)
t.lt(180 - ((180 - 360 / n) / 2))
t.fd(2 * l * math.sin((360 / n) /180 * math.pi / 2))
t.pu()
# 中心点不一定是原点，用下两句代替 home()方法
t.goto(x, y) # 使小乌龟回到中心点初始坐标
t.seth(0) # 使小乌龟转向向水平向右
t.pd()
pie_chart(bob, 100, 6)
bob.pu()
bob.setx(-300) # 中心点从原点左移300像素
bob.pd()
pie_chart(bob, 100, 5)
bob.pu()
bob.setx(300) # 中心点从原点右移300像素
bob.pd()
pie_chart(bob, 100, 7)
bob.ht()
turtle.mainloop()
- 结果分析：
- home() 方法仅适合于小乌龟回到原点并转向初始方向，本变形练习中的饼图中心点不全是原点，所以原练习中所用方法 home() 不再适合在此使用；
- Turtle 对象移动到指定坐标和转向指定角度的方法：
- setx(100)：移动到横向坐标100（像素）
- sety(100)：移动到纵向坐标100（像素）
- goto(100, 100)：移动到横向坐标100、纵向坐标100的点
- seth(90)：转向90度方向
习题4-4：用函数绘制字母
【习题】 字母表中的字母可以由少量基本元素构成，例如竖线和横线，以及一些曲线。 设计一种可用由最少的基本元素绘制出的字母表，然后编写能画出各个字母的函数，为每个字母写一个函数，起名为draw_a，draw_b等等， 然后将函数放在一个名为 letters.py 的文件里
- 练习记录：
import turtle
# 从自定义模块 polygon 中 import circle,arc等函数
from polygon import circle, arc
# 0 级基本体
# fd, bk, lt, rt, pu, pd
def fd(t, length):
t.fd(length)
def bk(t, length):
t.bk(length)
def lt(t, angle=90):
t.lt(angle)
def rt(t, angle=90):
t.rt(angle)
def pd(t):
t.pd()
def pu(t):
t.pu()
# 1 级基本体：0 级基本体的简单组合
def fdlt(t, n, angle=90):
fd(t, n)
lt(t, angle)
def fdbk(t, n):
fd(t, n)
bk(t, n)
def skip(t, n):
pu(t)
fd(t, n)
pd(t)
def stump(t, n, angle=90):
lt(t)
fd(t, n)
rt(t, angle)
def hollow(t, n):
lt(t)
skip(t, n)
rt(t)
# 2 级基本体
def post(t, n):
lt(t)
fdbk(t, n)
rt(t)
def beam(t, n, height):
hollow(t, n*height)
fdbk(t, n)
hollow(t, -n*height)
def hangman(t, n, height):
stump(t, n * height)
fdbk(t, n)
lt(t)
bk(t, n*height)
rt(t)
def diagonal(t, x, y):
from math import atan2, sqrt, pi
angle = atan2(y, x) * 180 / pi
dist = sqrt(x**2 + y**2)
lt(t, angle)
fdbk(t, dist)
rt(t, angle)
def vshape(t, n, height):
diagonal(t, -n/2, height*n)
diagonal(t, n/2, height*n)
def bump(t, n, height):
stump(t, n*height)
arc(t, n/2.0, 180)
lt(t)
fdlt(t, n*height+n)
"""
字母的绘制功能都有前提条件，乌龟在字母的左下角，后置条件是海龟在右下角，面对它开始的方向；它们都以Turtle 对象作为第一个参数，以 size 作为第二个参数；大多数字母宽 n 个像素，高 2n 个像素
"""
def draw_a(t, n):
diagonal(t, n/2, 2*n)
beam(t, n, 1)
skip(t, n)
diagonal(t, -n/2, 2*n)
def draw_b(t, n):
bump(t, n, 1)
bump(t, n, 0)
skip(t, n/2)
def draw_c(t, n):
hangman(t, n, 2)
fd(t, n)
def draw_d(t, n):
bump(t, 2*n, 0)
skip(t, n)
def draw_ef(t, n):
hangman(t, n, 2)
hangman(t, n, 1)
def draw_e(t, n):
draw_ef(t, n)
fd(t, n)
def draw_f(t, n):
draw_ef(t, n)
skip(t, n)
def draw_g(t, n):
hangman(t, n, 2)
fd(t, n/2)
beam(t, n/2, 2)
fd(t, n/2)
post(t, n)
def draw_h(t, n):
post(t, 2*n)
hangman(t, n, 1)
skip(t, n)
post(t, 2*n)
def draw_i(t, n):
beam(t, n, 2)
fd(t, n/2)
post(t, 2*n)
fd(t, n/2)
def draw_j(t, n):
beam(t, n, 2)
arc(t, n/2, 90)
fd(t, 3*n/2)
skip(t, -2*n)
rt(t)
skip(t, n/2)
def draw_k(t, n):
post(t, 2*n)
stump(t, n, 180)
vshape(t, 2*n, 0.5)
fdlt(t, n)
skip(t, n)
def draw_l(t, n):
post(t, 2*n)
fd(t, n)
def draw_n(t, n):
post(t, 2*n)
skip(t, n)
diagonal(t, -n, 2*n)
post(t, 2*n)
def draw_m(t, n):
post(t, 2*n)
draw_v(t, n)
post(t, 2*n)
def draw_o(t, n):
skip(t, n)
circle(t, n)
skip(t, n)
def draw_p(t, n):
bump(t, n, 1)
skip(t, n/2)
def draw_q(t, n):
draw_o(t, n)
diagonal(t, -n/2, n)
def draw_r(t, n):
draw_p(t, n)
diagonal(t, -n/2, n)
def draw_s(t, n):
fd(t, n/2)
arc(t, n/2, 180)
arc(t, n/2, -180)
fdlt(t, n/2, -90)
skip(t, 2*n)
lt(t)
def draw_t(t, n):
beam(t, n, 2)
skip(t, n/2)
post(t, 2*n)
skip(t, n/2)
def draw_u(t, n):
post(t, 2*n)
fd(t, n)
post(t, 2*n)
def draw_v(t, n):
skip(t, n/2)
vshape(t, n, 2)
skip(t, n/2)
def draw_w(t, n):
draw_v(t, n)
draw_v(t, n)
def draw_x(t, n):
diagonal(t, n, 2*n)
skip(t, n)
diagonal(t, -n, 2*n)
def draw_v(t, n):
skip(t, n/2)
diagonal(t, -n/2, 2*n)
diagonal(t, n/2, 2*n)
skip(t, n/2)
def draw_y(t, n):
skip(t, n/2)
stump(t, n)
vshape(t, n, 1)
rt(t)
fdlt(t, n)
skip(t, n/2)
def draw_z(t, n):
beam(t, n, 2)
diagonal(t, n, 2*n)
fd(t, n)
def draw_(t, n):
skip(t, n)
# 调用函数绘制汉语拼音 NIHAO
size = 20
bob = turtle.Turtle()
bob.pu()
bob.bk(100)
bob.pd()
draw_n(bob, size) # 画 N
skip(bob, size)
draw_i(bob, size) # 画 I
skip(bob, size)
draw_h(bob, size) # 画 H
skip(bob, size)
draw_a(bob, size) # 画 A
skip(bob, size)
draw_o(bob, size) # 画 O
skip(bob, size)
turtle.mainloop()
- 结果分析：
- 分级抽象归纳出基本体，并编写出自定义函数，供上一级调用，到画字母共分了4级
- 在画 O 和 Q 的函数 draw_o 、draw_q 中调用了 circle 函数、 在画 S 的函数 draw_s 中调用了 arc 函数，这两个函数都在自定义模块 polygon 中，该模块文件 polygon.py（提取码：9588） 必须与 letters.py 放在同一个文件夹中，circle 、 arc 才能在 letters.py 中被 import
习题4-5：用函数绘制螺线
【习题】 阅读螺线（spiral）的相关知识； 然后编写一个绘制阿基米德螺线（或者其他种类的螺线）的程序
- 练习记录：
import math
import turtle
bob = turtle.Turtle()
sam = turtle.Turtle()
alice = turtle.Turtle()
# 画直角坐标线
alice.bk(200)
alice.fd(400)
sam.lt(90)
sam.bk(200)
sam.fd(400)
# 定义画阿基米德螺线函数 Achimedean_spiral
def Achimedean_spiral(t, a, b):
"""
阿基米德螺线公式：r = a + θ*b
"""
r1 = a # 初始点与中心点距离 r1
theta = 0 # 螺线转动到的角度，初值赋为 0，改变此初值可改变螺线偏转角度
# 小乌龟移到第一笔起始点
t.pu()
t.goto(a * math.cos(theta / 180 * math.pi), a * math.sin(theta / 180 * math.pi))
t.pd()
alfa = 3 # 每一笔螺线转3度，改变此值可改变精度
n = 240 # 画240笔
for i in range(n):
theta = theta + alfa
r2 = r1 + (alfa / 180 * math.pi) * b # 每一笔终点与中心点距离 r2
# 计算每一笔终点直角坐标(x, y)
x = r2 * math.cos(theta / 180 * math.pi)
y = r2 * math.sin(theta / 180 * math.pi)
t.goto(x, y) # (x, y)为每一笔终点直角坐标
t.seth(theta + 90) # 使笔与终点到中心点连线垂直
r1 = r2 # 把每一笔终点与中心点距离 r2 赋值给下一笔起始点与中心点距离 r1
# 调用画阿基米德螺线函数 Achimedean_spiral
Achimedean_spiral(bob, 0, 10)
turtle.mainloop()
- 结果分析：
-
画阿基米德螺线函数 Achimedean_spiral（用极坐标转换直角坐标的方法画阿基米德螺线） ：把每一笔终点极坐标（r2, theta）转换成直角坐标 (x, y) ，再用 goto(x, y) 方法画起点到终点的线段，如下图：
-
Achimedean_spiral函数定义时：
- 改变 theta 初始值，可改变螺线偏转方向
- 改变 n 值，可改变螺线长度
- 改变 alfa 值，可改变螺线精度
-
Turtle 对象的 goto() 方法：定位并前往
-
练习中，输入的实参 a 即起始点与中心点距离为 0 ，所画的螺线是中心点与起始点重合的特例，也可以输入其他大于零的数
-
- 变形练习：（定义一个函数，用类似教材中画多边形的函数 polygon 中的方法画阿基米德螺线）
import math
import turtle
bob = turtle.Turtle()
tom = turtle.Turtle()
sam = turtle.Turtle()
alice = turtle.Turtle()
# 画直角坐标线
alice.bk(200)
alice.fd(400)
sam.lt(90)
sam.bk(200)
sam.fd(400)
# 定义画阿基米德螺线函数 Achimedean_spiral
def Achimedean_spiral(t, a, b):
"""
阿基米德螺旋线公式：r = a + θ*b
"""
r1 = a # 初始点与中心点距离 r1
theta = 60 # 螺线转动到的角度，初值赋为 60，改变此初值可改变螺线偏转角度
alfa = 3 # 每一笔螺线转3度，改变此值可改变精度
# 小乌龟移到第一笔起始点
t.pu()
t.goto(a * math.cos(theta /180 * math.pi), a * math.sin(theta / 180 * math.pi))
t.pd()
n = 240 # 画240笔
for i in range(n):
theta = theta + alfa
r2 = r1 + (alfa / 180 * math.pi) * b # 每一笔终点与中心点距离 r2
# 计算每一笔终点直角坐标 (x, y)
x = r2 * math.cos(theta / 180 * math.pi)
y = r2 * math.sin(theta / 180 * math.pi)
t.goto(x, y) # (x, y)为每一笔终点直角坐标
t.seth(theta + 90) # 使笔与终点到中心点连线垂直，与下一笔方向并不完全一致
r1 = r2 # 把每一笔终点与中心点距离 r2 赋值给下一笔起始点与中心点距离 r1
# 定义画阿基米德螺线函数 Achimedean_spiral_2
def Achimedean_spiral_2(t, a, b):
"""
阿基米德螺旋线公式：r = a + θ*b
"""
r1 = a # 初始点与中心点距离 r1
theta = 60 # 螺线转动到的角度，初值赋为60，改变此初值可改变螺线偏转角度
alfa = 3 # 设定每一笔螺线转3度，改变此值可改变螺线精度
# 小乌龟移到第一笔起始点
t.pu()
t.goto(a * math.cos(theta /180 * math.pi) , a * math.sin(theta / 180 * math.pi))
t.pd()
n = 180 # 画180笔
for i in range(n):
r2 = r1 + (alfa / 180 * math.pi) * b
l = math.sqrt(r1*r1 + r2*r2 - 2 * math.cos(alfa / 180 * math.pi) * r1 * r2)
if r1 == 0:
orientation = theta + alfa # 计算 a=0 时第一笔的朝向
else:
beta = math.acos((r1**2 + l**2 - r2**2) / (2 * r1 * l)) / math.pi * 180 # 根据余弦定理计算 beta（ beta 见习题结果分析）
orientation = theta + 180 - beta
t.seth(orientation)
t.fd(l)
theta = theta + alfa
r1 = r2
# 调用画阿基米德螺线函数 Achimedean_spiral
bob.pencolor(0,0,1)
Achimedean_spiral(bob, 0, 10)
# 调用画阿基米德螺线函数 Achimedean_spiral_2
tom.pencolor(1,0,0)
Achimedean_spiral_2(tom, 0, 10)
turtle.mainloop()
-
结果分析：
-
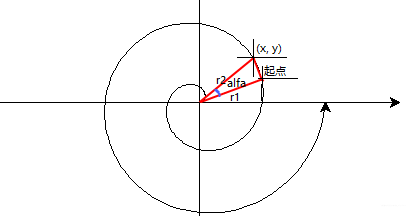
画阿基米德螺线函数 Achimedean_spiral_2（用类似教材中画多边形的函数 polygon 中的方法画阿基米德螺线） ：用余弦定理计算画每一笔线段的长度 l 和用余弦定理计算角 beta 值及每一笔线段的朝向角 orientation ，再用 seth(orientation) 和 fd(l) 方法从起点画线段，如下图：
-
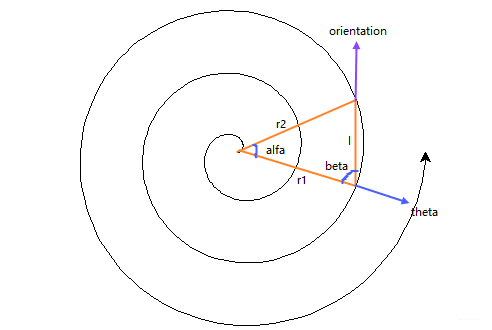
调用函数 Achimedean_spiral_2 与 调用函数 Achimedean_spiral 所画的（分别为红色和蓝色）的螺线完全重合，说明只要方法正确，计算机都会给你正确结果
-
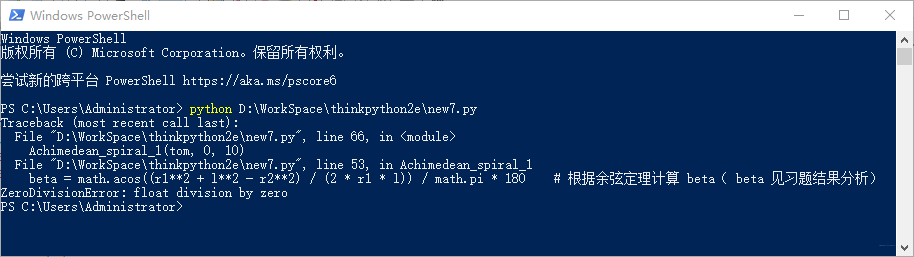
但用余弦定理计算 beta 及 orientation 时，有个特例会出现报错，如下图：
从终端信息“ZeroDivisionError: float division by zero”可以看出，在运行到计算 beta 值的语句时出现了浮点数除以0的错误；分析该语句中的除法运算，显然是 r1 出现了为0的情况，而 r1 为0的情况只有在起始点与中心点重合（即 a 为0）且画第一笔时才会出现；定义函数 Achimedean_spiral_2 时须对 r1 为0的情况作例外处理以避免出现上述错误
-
对边界数据的复核检验、边界情况的例外处理，是编程人员应有的思维方式，是编程过程中的例行事务
-