【力扣周赛】第340场周赛
【力扣周赛】第340场周赛
-
- 6361:对角线上的质数
-
- 题目描述
- 解题思路
- 6360:等值距离和
-
- 题目描述
- 解题思路
6361:对角线上的质数
题目描述
描述:给你一个下标从 0 开始的二维整数数组 nums ,返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数,返回 0 。
注意:
1、如果某个整数大于 1 ,且不存在除 1 和自身之外的正整数因子,则认为该整数是一个质数。
2、如果存在整数 i ,使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ,则认为整数 val 位于 nums 的一条对角线上。
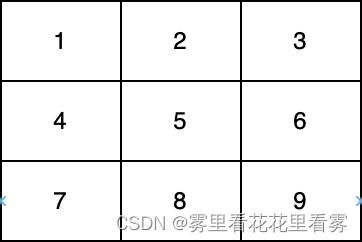
在上图中,一条对角线是 [1,5,9] ,而另一条对角线是 [3,5,7] 。
1 <= nums.length <= 300。
nums.length == numsi.length。
1 <= nums[i][j] <= 4*106。
输入:nums = [[1,2,3],[5,6,7],[9,10,11]]
输出:11
解释:数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数,故返回 11 。
输入:nums = [[1,2,3],[5,17,7],[9,11,10]]
输出:17
解释:数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数,故返回 17 。
解题思路
难度:简单。
思路:首先编写一个判断是否为质数的函数,然后遍历矩阵,当遇到对角线元素时,如果其为质数则更新最大质数值。
// 判断是否为质数
bool isPrime(int n)
{
if(n==1)
return false;
if(n<=3)
return true;
int i;
for(i=2;i<=sqrt(n);i++)
if(n%i==0)
break;
if(i>sqrt(n))
return true;
return false;
}
int diagonalPrime(vector<vector<int>>& nums) {
// 存储结果
int res=0;
// 记录长度
int n=nums.size();
// 遍历对角线
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if((i+j==(n-1))||(i==j))
{
if(isPrime(nums[i][j]))
res=max(res,nums[i][j]);
}
return res;
}
6360:等值距离和
题目描述
描述:给你一个下标从 0 开始的整数数组 nums 。现有一个长度等于 nums.length 的数组 arr 。对于满足 nums[j] == nums[i] 且 j != i 的所有 j ,arr[i] 等于所有 |i - j| 之和。如果不存在这样的 j ,则令 arr[i] 等于 0 。
返回数组 arr 。
输入:nums = [1,3,1,1,2]
输出:[5,0,3,4,0]
解释:
i = 0 ,nums[0] == nums[2] 且 nums[0] == nums[3] 。因此,arr[0] = |0 - 2| + |0 - 3| = 5 。
i = 1 ,arr[1] = 0 因为不存在值等于 3 的其他下标。
i = 2 ,nums[2] == nums[0] 且 nums[2] == nums[3] 。因此,arr[2] = |2 - 0| + |2 - 3| = 3 。
i = 3 ,nums[3] == nums[0] 且 nums[3] == nums[2] 。因此,arr[3] = |3 - 0| + |3 - 2| = 4 。
i = 4 ,arr[4] = 0 因为不存在值等于 2 的其他下标。
输入:nums = [0,5,3]
输出:[0,0,0]
解释:因为 nums 中的元素互不相同,对于所有 i ,都有 arr[i] = 0 。
解题思路
难度:中等。
思路:双重循环。外层循环遍历当前数组元素,内层循环遍历从当前数组元素后一个元素开始的剩余数组元素,如果两者相等,则将两者的下标绝对值和分别加到两者对应的结果数组元素上。时间复杂度为O(n2),超出时间限制。
vector<long long> distance(vector<int>& nums)
{
int n=nums.size();
vector<long long> res(n,0);
for(int i=0;i<n;i++)
// 保证i和j不相等
for(int j=i+1;j<n;j++)
{
if(nums[i]==nums[j])
{
res[i]+=abs(j-i);
res[j]+=abs(j-i);
}
}
return res;
}
优化:不妨直接使用map将相同元素进行分组处理,即map存储数值以及数值对应的下标列表。首先遍历数组,当在map中未找到当前数组元素时则直接将其加入map,反之则遍历当前数组元素所对应的下标列表,然后依次计算各个元素与当前元素的下标绝对值之和,并将其分别加到当前下标列表元素与当前元素上。虽然但是,还是超出时间限制。
vector<long long> distance(vector<int>& nums)
{
int n=nums.size();
vector<long long> res(n,0);
map<int,vector<int>> umap;
// 将值相同的下标均加入map
for(int i=0;i<n;i++)
{
if(umap[nums[i]].size()!=0)
{
for(int j=0;j<umap[nums[i]].size();j++)
{
int diff=i-umap[nums[i]][j];
res[i]+=diff;
res[umap[nums[i]][j]]+=diff;
}
}
umap[nums[i]].push_back(i);
}
return res;
}
优化:前缀和与后缀和公式。假设当前位置下标为i,当前位置元素与前面所有位置元素的差绝对值和为left[i],当前位置元素与后面所有位置元素的差绝对值和为right[i],当前位置元素与其他所有位置元素的差绝对值和为sum[i],其计算公式如下。
left[i]=left[i-1]+i*(arr[i]-arr[i-1])
right[i]=right[i+1]+(n-i-1)*(arr[i+1]-arr[i])
sum[i]=left[i]+right[i]
思路:综上所述,整体解题思路如下,首先使用map将相同元素进行分组处理,即map存储数值以及数值对应的下标列表,然后遍历map,对于每一个分组,计算下标列表各个元素的前缀和以及后缀和,再计算各个元素的前缀和后缀和,并将其加入到结果数组中。
vector<long long> distance(vector<int>& nums)
{
int n=nums.size();
vector<long long> res(n,0);
unordered_map<int,vector<int>> umap;
// 将所有相同值元素下标分组存储
for(int i=0;i<n;i++)
umap[nums[i]].push_back(i);
// 遍历umap
for(auto it:umap)
{
int m=it.second.size();
// 存储前缀和
vector<long long> left(m,0);
// 存储后缀和
vector<long long> right(m,0);
// 计算前缀和 第一个元素前缀和为0
for(int i=1;i<m;i++)
left[i]=left[i-1]+i*(it.second[i]-it.second[i-1]);
// 计算后缀和 最后一个元素后缀和为0
for(int i=m-2;i>=0;i--)
right[i]=right[i+1]+(m-i-1)*(it.second[i+1]-it.second[i]);
// 计算前缀和后缀和
for(int i=0;i<m;i++)
res[it.second[i]]=left[i]+right[i];
}
return res;
}
第一场周赛,只写出来了两题,打击自信哈哈哈哈,再接再厉吧~