【大数据竞赛】2022MathorCup大数据挑战赛 B题 北京移动用户体验影响因素研究 探索性数据分析
系列文章目录
第一章 【大数据竞赛】2022MathorCup大数据竞赛 B题 北京移动用户体验影响因素研究 题目分析
第二章【大数据竞赛】2022MathorCup大数据挑战赛 B题 北京移动用户体验影响因素研究 探索性数据分析
文章目录
- 系列文章目录
- 前言
- 一、准备阶段
-
- 1.数据准备
- 2.导入依赖包
- 3.导入数据
- 二、探索性数据分析
-
- 1.变量识别
- 2.单变量分析
- 2.双变量分析
- 总结
前言
该系列文章分为问题分析、探索性数据分析、特征工程、模型建立四个部分,以此来记录完成本次竞赛的具体思路,及对部分问题的补充研究。
探索性数据分析(EDA)主要包括三部分:变量识别、单变量分析、双变量分析,具体概述可查看【EDA与特征工程】数据探索与特征工程综合指南,本文对附件一数据进行探索性分析进行记录,对竞赛思路的回顾和补充。
若需要附件数据,评论区留邮箱,看到会回复。
一、准备阶段
1.数据准备
将原始数据转换为csv文件格式,保存到data路径,方便之后操作。
import pandas as pd
import openpyxl
import os
# 创建一个data文件夹,用于存放csv格式的数据
if not os.path.exists('D:\\Jupyter\\Competition\\20221220_bigdata\\初赛赛题 2022年MathorCup大数据竞赛\\2022年MathorCup大数据竞赛-赛道B初赛\\data'):
os.makedirs('D:\\Jupyter\\Competition\\20221220_bigdata\\初赛赛题 2022年MathorCup大数据竞赛\\2022年MathorCup大数据竞赛-赛道B初赛\\data')
df1 = pd.read_excel('D:\\Jupyter\\Competition\\20221220_bigdata\\初赛赛题 2022年MathorCup大数据竞赛\\2022年MathorCup大数据竞赛-赛道B初赛\\附件1语音业务用户满意度数据.xlsx',
engine='openpyxl').iloc[:,:55]
df1.to_csv('D:\\Jupyter\\Competition\\20221220_bigdata\\初赛赛题 2022年MathorCup大数据竞赛\\2022年MathorCup大数据竞赛-赛道B初赛\\data\\附件1语音业务用户满意度数据.csv',
sep=',',index=False,encoding='utf_8_sig')
# 设置工作路径
os.chdir('D:\\Jupyter\\Competition\\20221220_bigdata\\初赛赛题 2022年MathorCup大数据竞赛\\2022年MathorCup大数据竞赛-赛道B初赛'')
2.导入依赖包
# 导入依赖包
import pandas as pd
import numpy as np
import missingno as msno
import scipy.stats as st
import matplotlib.pyplot as plt
import seaborn as sns
# 设置图像样式
plt.style.use('seaborn-darkgrid')
sns.set(style = 'darkgrid')
# 设置图像字体
plt.rcParams['font.sans-serif'] = ['STSong']
# 忽略警告
import warnings
warnings.filterwarnings('ignore')
# 显示pd所有列
pd.set_option('display.max_columns', None)
3.导入数据
# 导入数据
data1=pd.read_csv('./data/附件1语音业务用户满意度数据.csv', index_col= '用户id')
# 查看前五行
data1.head()
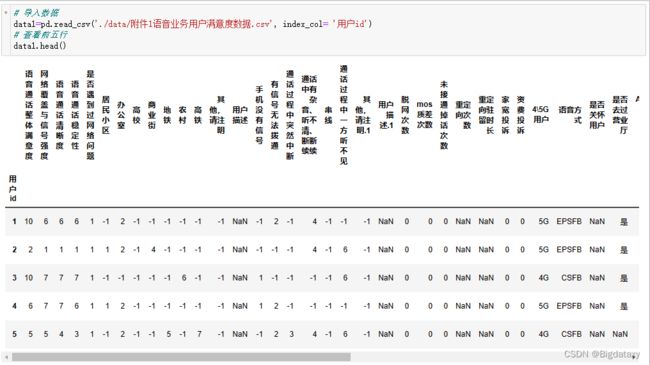
# 结合附件5对数据作基本处理
data1['重定向次数']=data1['重定向次数'].fillna(value=0)
data1['重定向驻留时长']=data1['重定向驻留时长'].fillna(value=0)
data1['是否关怀用户']=data1['是否关怀用户'].fillna(value='否')
data1['是否去过营业厅']=data1['是否去过营业厅'].fillna(value='否')
二、探索性数据分析
1.变量识别
# 查看数据基本信息
data1.info()
print(f"附件1语音业务用户满意度数据的原始数据形状为:{data1.shape}")
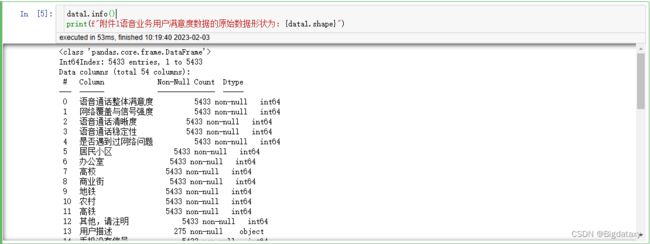
通过题目背景及查看数据基本信息,可将前4个变量划分为目标变量,其余50个划分为预测变量;对于预测变量数据类型,将数据划分为对象数据类型,整数类型以及浮点类型;对于预测变量数据类别,将数据划分为分类变量与连续变量。该数据中有几列属性表示次数,即整数类型中有部分表示为分类变量(0-1),有部分表示为连续变量(次数),即将整数类型中的连续变量划分到浮点类型中,代码如下:
#对数据列属性进行分类,int,float,subject,方便后续对应编码操作
import numpy as np
#判断数据类型函数2
def pd_sjlx(data):#object,float64,int64
fds=[]#浮点数
lb=[]#类别中,英文
zs=[]#整数
for name in data.columns.tolist():
if(data[name].dtype==object):
lb.append(name)
if(data[name].dtype==np.float64 or data[name].dtype==np.float32):
fds.append(name)
if(data[name].dtype==np.int64 or data[name].dtype==np.int32):
if((len(data[name].unique())>10)):#设置阈值为10,判断是否为整数类型的连续数值变量
fds.append(name)
else:
zs.append(name)
return lb,fds,zs
lb,fds,zs=pd_sjlx(data1.iloc[:,4:])
print('类别列',lb)
print()
print('数值列',fds)
print()
print('类别数值列',zs)

2.单变量分析
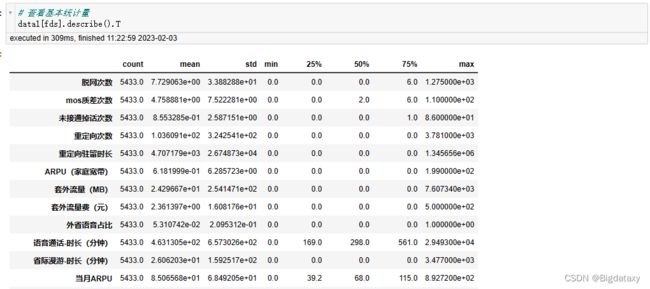
对于连续变量进行单变量分析,需要了解变量的集中趋势、扩散程度及分布。查看其基本统计量如下:
# 查看基本统计量
data1[fds].describe().T
dis_cols = 5 #一行几个
dis_rows = len(fds)
plt.figure(figsize=(7*dis_cols, 4* dis_rows))
for i in range(len(fds)):
ax = plt.subplot(dis_rows, dis_cols, i+1)
ax = sns.kdeplot(data1.loc[:,fds[i]], shade= True)
ax.set_xlabel(fds[i],fontsize= 15)
ax.set_ylabel("Frequency", fontsize= 15)
plt.tight_layout()
plt.show()

由上图可知,个别属性大致呈现正态分布,其他整体呈现左偏分布,后续可考虑平方/立方或指数对变量进行转换。
对于分类变量进行单变量分析,使用频率表来了解每个类别的分布,这里针对目标变量进行频数可视化分析。
# 查看各因变量的类别频数
fig = plt.figure(figsize = (16,9), dpi= 100)
fig.add_subplot(2,2,1)
sns.countplot(x='语音通话整体满意度',data=data1)
fig.add_subplot(2,2,2)
sns.countplot(x='网络覆盖与信号强度',data=data1)
fig.add_subplot(2,2,3)
sns.countplot(x='语音通话清晰度',data=data1)
fig.add_subplot(2,2,4)
sns.countplot(x='语音通话稳定性',data=data1)
# plt.savefig('./图片/满意度各类别频数统计图',formate='png',dpi=500)

2.双变量分析
双变量分析是找出两个变量之间的关系。在预定义的显著性水平上寻找变量之间的关联和分离。我们可以对分类变量和连续变量的任意组合进行双变量分析。组合可以是:分类和分类,分类和连续以及连续和连续。
- 分类和分类:本次竞赛我们将满意度作为分类变量,这里主要分析目标变量之间的关系。

由上图可得,当其中一个目标变量评分较高时,其余变量评分大概率较高,但也有个别样本的某一目标变量与其他目标变量取值差异较大,这些样本可能含有重要区分信息。
# 因变量满意度交叉分析
fig = plt.figure(figsize = (24,5), dpi= 100)
fig.add_subplot(1,3,1)
sns.barplot(x='网络覆盖与信号强度',y='语音通话整体满意度',data=data1)
fig.add_subplot(1,3,2)
sns.barplot(x='语音通话清晰度',y='语音通话整体满意度',data=data1)
fig.add_subplot(1,3,3)
sns.barplot(x='语音通话稳定性',y='语音通话整体满意度',data=data1)
#plt.savefig('./图片/满意度交叉分析',formate='png',dpi=500)
sns.pairplot(data1.iloc[:,:4],hue='语音通话整体满意度')
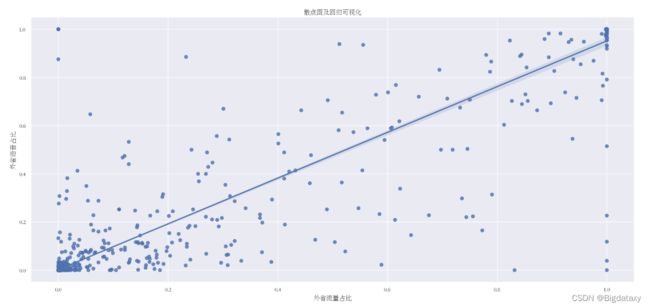
- 连续与连续:在两个连续变量之间进行双变量分析时,应该查看散点图。通过前面单变量分析中的密度图,观测【“外省流量占比”,“外省语音占比”】两者分布大致相同,此处讨论两者的关系。
plt.figure(figsize=(20,9),dpi= 100)
sns.regplot(x= data1['外省流量占比'], y= data1['外省语音占比'])
plt.title('散点图及回归可视化')
plt.show()
pd.concat([data1['外省流量占比'],data1['外省语音占比']], axis= 1).corr(method= "pearson")
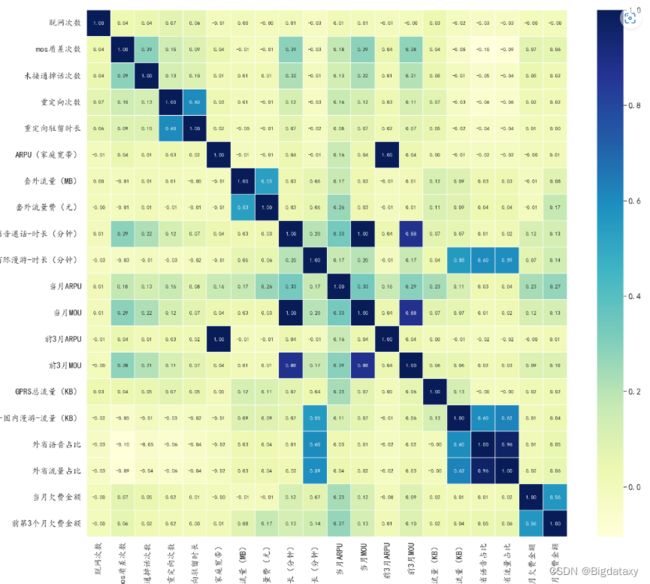
fig = plt.figure(figsize = (20,18))
sns.heatmap(data1[col].corr(),cmap='YlGnBu',linewidth=0.5,annot=True,fmt='.2f')#数值变量相关系数
总结
本次竞赛在探索性数据分析部分做的不够完整,变量识别做的较好,单变量分析及多变量分析仅做了少部分较为主要的特征,还有许多其他特征没有考虑全面或根本没有考虑到,并且连续变量与分类变量的关系没有进行系统的探索(当时这一环节一直纠结于选择的方法)。