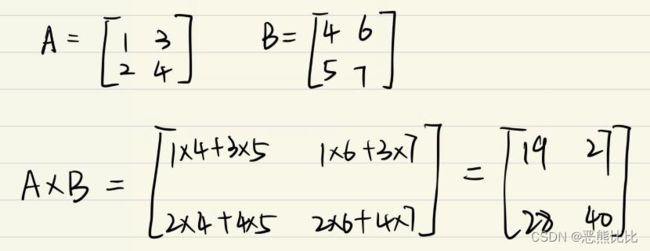Python实现向量、矩阵运算(dot点积运算)
1.点积运算概念
点积运算是参与运算的两向量各对应位置上元素相乘后,再将各乘积相加。
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:
a·b=a1b1+a2b2+……+anbn。
.
使用矩阵乘法,点积还可以写为:a·b=(a^T )*b
// 这里的a^T指示矩阵a的转置。
numpy库的使用:https://blog.csdn.net/weixin_45627039/article/details/124237992
2. python中实现一维向量的方法
A = [7,2,3,5,6]
B = [1,5,9,6,3]
方法1(分支语句for 循环计算):
A = [7,2,3,5,6]
B = [1,5,9,6,3]
c = 0
for i in range(len(A)):
c += A[i]*B[i]
print(c) #92
方法2 (dot函数)
import numpy as np
A = np.array([7,2,3,5,6])
B = np.array([1,5,9,6,3])
print(np.dot(A,B)) #92
2. python中实现二维向量的方法
A = [[1,3],[2,4]]
B = [[4,6],[5,7]]
方法1(分支语句for 循环计算):
A = [[1,3],[2,4]]
B = [[4,6],[5,7]]
c = [[0 for i in range (len(A[0]))]for j in range(len(B))]
for i in range(len(A)):
for j in range(len(A[i])):
for k in range(len(B)):
c[i][j] += A[i][k]*B[k][j]
print(c) #[[19, 27], [28, 40]]
方法2 (dot函数)
import numpy as np
A = [[1,3],[2,4]]
B = [[4,6],[5,7]]
A = np.array(A)
B = np.array(B)
print(np.dot(A,B))
#[[19 27]
#[28 40]]