力扣刷题笔记 栈与队列篇

总结先放在前面：

栈和队列是可以互相转换使用的，其中两个栈可以实现一个队列，而一个队列就可以实现栈。
栈通常用来解决匹配问题，比如说NO.20. 有效的括号和NO.1047. 删除字符串中的所有相邻重复项以及NO.150. 逆波兰表达式求值
对于队列，应该通过 NO.239. 滑动窗口最大值 来学习单调队列（实际上由于C#不像C++或者java一样有方法可以获取队列的末尾值getLast()和removeLast()之类的方法，我们需要使用List来进行替代），这里主要是学习它的想法

解答栈与队列时的一些小技巧与注意点：

栈对于在遇到字符串以及一个有关于处理优先级顺序方面的题目很有用，比如说括号匹配，逆波兰表达式
队列需要学会单调队列的思想，NO.239. 滑动窗口最大值 主要提示了队列在窗口类题目的应用

题目实战

1.NO.232.用栈实现队列

public class MyQueue {

    Stack<int> st1=new Stack<int>(); //st1用来保存数据
    Stack<int> st2=new Stack<int>(); //st2用来保存顺序排好的数据
    /** Initialize your data structure here. */
    public MyQueue() {

    }
    
    /** Push element x to the back of queue. */
    public void Push(int x) { //
        st1.Push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    public int Pop() {
        while(st1.Count!=0){
            st2.Push(st1.Pop());
        }
        int tmp=st2.Pop();
        while(st2.Count!=0){
            st1.Push(st2.Pop());
        }
        return tmp;
    }
    
    /** Get the front element. */
    public int Peek() { //队列开头的元素，就是栈最底下的元素。
        while(st1.Count!=0){    //把st1全部压到st2中，顺序就对了
            st2.Push(st1.Pop());
        }
        int tmp= st2.Peek();
        while(st2.Count!=0){    //复原
            st1.Push(st2.Pop());
        }
        return tmp;
    }
    
    /** Returns whether the queue is empty. */
    public bool Empty() {
        if(st1.Count==0){
            return true;
        }
        return false;
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.Push(x);
 * int param_2 = obj.Pop();
 * int param_3 = obj.Peek();
 * bool param_4 = obj.Empty();
 */

2.NO.225. 用队列实现栈

其实队列实现一个栈只需要知道队列里面有多少个元素就行了，通过不断地出和进来改变顺序

public class MyStack {
    Queue<int> que=new Queue<int>();
    int count=0; //count用来保存当前队列中元素的个数
    /** Initialize your data structure here. */
    public MyStack() {

    }
    
    /** Push element x onto stack. */
    public void Push(int x) {
        que.Enqueue(x);
        count++;
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int Pop() {
        for(int i=0;i<count-1;i++){
            que.Enqueue(que.Dequeue());
        }
        count--;
        return que.Dequeue();
    }
    
    /** Get the top element. */
    public int Top() {
        for(int i=0;i<count-1;i++){
            que.Enqueue(que.Dequeue());
        }
        int tmp=que.Dequeue();
        que.Enqueue(tmp);
        return tmp;
    }
    
    /** Returns whether the stack is empty. */
    public bool Empty() {
        if(count==0){
            return true;
        }
        return false;
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.Push(x);
 * int param_2 = obj.Pop();
 * int param_3 = obj.Top();
 * bool param_4 = obj.Empty();
 */

3.NO.20. 有效的括号

这里需要注意一下，C#中if语句是有优先级的，顺序是从左往右
这道题中，需要考虑stack为空的情况，如果

if(st.Count==0||st.Peek()!='(')

的顺序颠倒一下，改为

if(st.Peek()!='('||st.Count==0)

的话，if语句由于会先执行st.Peek()!=’('的判断而报错栈空
代码方面思路可见注释

public class Solution {
    public bool IsValid(string s) {
        Stack<char> st=new Stack<char>();
        for(int i=0;i<s.Length;i++){
            
            if(s[i]==')'){  //如果出现左半边，由于需要以正确顺序闭合
                if(st.Count==0||st.Peek()!='('){ //上一个必须是它对应的左半边。并且需要考虑为空的情况
                    return false;
                }
                else{
                    st.Pop();
                }
            }
            

            else if(s[i]=='}'){  
                if(st.Count==0||st.Peek()!='{'){ 
                    return false;
                }
                else{
                    st.Pop();
                }
            }

            else if(s[i]==']'){  
                if(st.Count==0||st.Peek()!='['){ 
                    return false;
                }
                else{
                    st.Pop();
                }
            }

            else{
                st.Push(s[i]);
            }
        }

        if(st.Count==0){
            return true;
        }
        return false;
    }
}

4.NO.1047. 删除字符串中的所有相邻重复项

这道题几乎和上一题完全一样，基本没有变化，可以总结出规律了

public class Solution {
    public string RemoveDuplicates(string s) {
        Stack<char> st=new Stack<char>();
        for(int i=0;i<s.Length;i++){
            if(st.Count!=0&&s[i]==st.Peek()){
                st.Pop();
            }
            else{
                st.Push(s[i]);
            }
            
        }
        // string ans="";
        // foreach(char i in st){
        //     ans+=i;
        // }
        // string result = "";     //进行字符串反转
        // for (int i = ans.Length - 1; i >= 0; i--)
        // {						//一开始手写的字符串反转，发现时间和内存消耗较高，远高于平均水平
        //     result += ans[i];
        // }
        // return result;
            var b = a.Reverse();		//学习评论区的方法，大幅降低了时间和空间复杂度
            return new string(b.ToArray());
        
    }
}

5.NO.150. 逆波兰表达式求值

逆波兰表达式可以认为是只要遇到运算符就将它前面两个数据与运算符进行运算，然后将结果再次存储到栈中。栈本身就充当了一个括号的功能

public class Solution {
    public int EvalRPN(string[] tokens) {
        Stack<int> st=new Stack<int>();
        int num1=0; //这两个num用作临时存储用
        int num2=0;
        for(int i=0;i<tokens.Length;i++){
            if(tokens[i]=="+"){ //如果是运算符，说明要将这个运算符前面的两个值弹出来获取新的值
                num1=st.Pop();
                num2=st.Pop();
                st.Push(num2+num1); //需要注意一下顺序，先出的是被加数，后出的是加数
            }

            else if(tokens[i]=="-"){
                num1=st.Pop();
                num2=st.Pop();
                st.Push(num2-num1);
            }

            else if(tokens[i]=="*"){ 
                num1=st.Pop();
                num2=st.Pop();
                st.Push(num2*num1);
            }

            else if(tokens[i]=="/"){ 
                num1=st.Pop();
                num2=st.Pop();
                st.Push(num2/num1);
            }

            else {
                st.Push(int.Parse(tokens[i]));
            }

        }
        return st.Peek();
    }
}

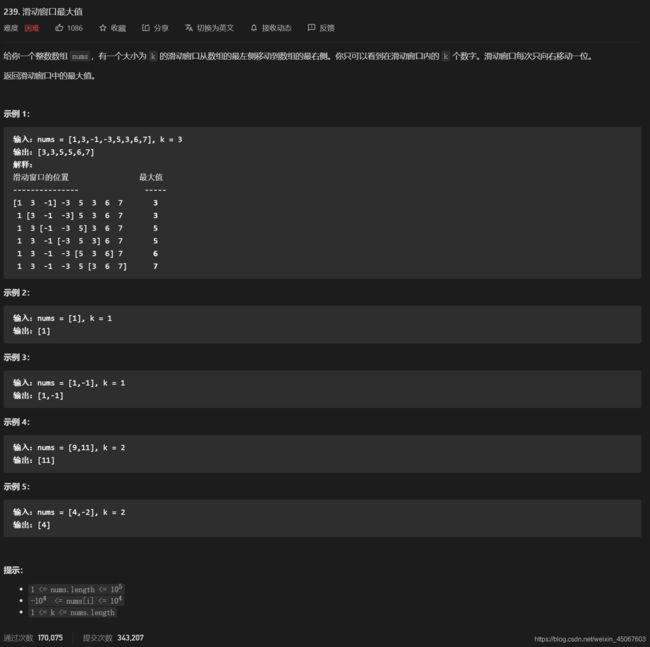
6.NO.239. 滑动窗口最大值

时间消耗感人，这道题学习思想更重要一些

public class Solution {
    //如果使用暴力解法的话，复杂度为O（N*k），会超时
    //为什么暴力方法效率低？因为每一次滑动窗口都对窗口内所有值进行了一次比较
    //这里其实是没有必要对前面已经比较过的数进行比较，从这个方面进行切入
    //也就是说，我们要在O(1)的时间复杂度之内找到窗口内的最大值
    //这里也就用到了单调队列

    public class myType{   //由于需要数组的值和下标，声明一个新类myType
        public int index;
        public int val;
        public myType(int _index,int _val){
            index=_index;
            val=_val;
        }
    }

        //注意，这里系统自带的队列肯定是无法满足我们的要求的，我们需要自己重新定义一个队列
        List<myType> mylist=new List<myType>();    //重点是下面实现队列内【自动】维护
        int cur=0;  //cur用来维护当前滑动窗口的左边界位置
        //首先思考我们需要的元素有哪些特征，也就是他们的优先级
        //因为是找最大值，那么数值大的数肯定要考虑
        //然后，因为窗口在不断后移，所以靠后的数，即使比前面的数小，我们也需要纳入考虑
        //同时也可以总结出，在当前窗口内，如果数A比数B小，而且数B在数A的后面出现，那么A可以直接出列
        //由于C#无法获取队列末尾元素，所以只能改用list实现，但是思想其实是一样的
        public int myPush(myType A,int k){

            cur=A.index-k+1;                               //这里已知窗口的左边界一定是当前下标-k+1
            if(mylist.Count!=0&&mylist[0].index<cur){      //首先检查这里是不是左边界是否溢出
                mylist.RemoveAt(0);
            }

            //新加入的节点一定比原先的节点下标更大
            //如果新加入节点值也更大，就可以将原来的值进行舍弃
            //这样也保证了在这个队列当中，队列首部一定是队列的最大值
            while(mylist.Count!=0&&A.val>=mylist.Last().val){
                mylist.RemoveAt(mylist.Count-1);
            }

            //从后往前进行遍历，因为C#中List删除节点之后会自动前移
            //如果比之前的大，说明不是单调递减的，将这个数移除
            mylist.Add(A);
            return mylist[0].val;
        }
    

    public int[] MaxSlidingWindow(int[] nums, int k) {
        int[] ans=new int[nums.Length-k+1];
        for(int j=0;j<k-1;j++){ //初始化，在当前窗口不完整时，前面几个其实可以暂时不管
            int tmp=myPush(new myType(j,nums[j]),k);
        }
        for(int i=0;i<ans.Length;i++){
            ans[i]=myPush(new myType(i+k-1,nums[i+k-1]),k);
        }
        return ans;
    }
}

另附上评论区双向链表的C#解法，用linkedlist实现双端队列使得队首元素维持队列最大值，其实大致思想是一致的
时间消耗是我写的方法的一半

public class Solution {
       public int[] MaxSlidingWindow(int[] nums, int k)
        {
           int n = nums.Length;
            int[] res = new int[n - k + 1];
            LinkedList<int> dq = new LinkedList<int>();
            for(int i=0;i<n;i++)
            {
                if(dq.Count!=0&&dq.First.Value<(i-k+1))
                {
                    dq.RemoveFirst();//超出窗口长度时删除队首
                }
                while(dq.Count!=0&&nums[i]>=nums[dq.Last.Value])
                {
                    dq.RemoveLast();//如果遍历的元素大于队尾元素就删除队尾
                }
                dq.AddLast(i);//添加
                if(i>=k-1)
                {
                    res[i - k + 1] = nums[dq.First.Value];//结果
                }
            }
            return res;
           
        }
}