备战蓝桥杯——搜索专题刷题日常
众所周知,搜索是蓝桥杯的热门考点之一,掌握好DFS和BFS对于我们提高蓝桥杯获奖概率和算法能力有很大帮助,下面让我们一起写几道搜索相关的题目~
切割方格
由题意得,我们可以发现切割出来的图形都是关于中心对称的,所以当移动到边界时则说明此时分割出来的图形关于中心对称,符合题意,则ans++,我们可以设定 (3,3)为中心点,从中心点开始出发,那么此时(x,y)关于中心点对称的点为(6-x,6-y),因此当(x,y)被搜索的时候,(6-x,6-y)就不能被搜索到,那么此时就要标志此点和中心点为1,代表已经走过了。
题目中说旋转对称属于同一种割法,那么一种分割方案绕着中心点顺时针旋转得到的方案和原来的方案是同一种。因此我们在DFS完之后的ans要除以4。
#include
using namespace std;
int g[7][7];
int ans;
int dx[4]={0,-1,1,0};
int dy[4]={-1,0,0,1};
void dfs(int x,int y)
{
if(x==0||x==6||y==0||y==6)
{
ans++;
return;
}
for(int i=0;i<4;i++)
{
int x1= x+dx[i];
int y1= y+dy[i];
if(g[x1][y1]!=1)
{
g[x1][y1]=1;
g[6-x1][6-y1]=1;
dfs(x1,y1);
g[6-x1][6-y1]=0;
g[x1][y1]=0;
}
}
}
int main()
{
g[3][3]=1;
dfs(3,3);
cout< BFS
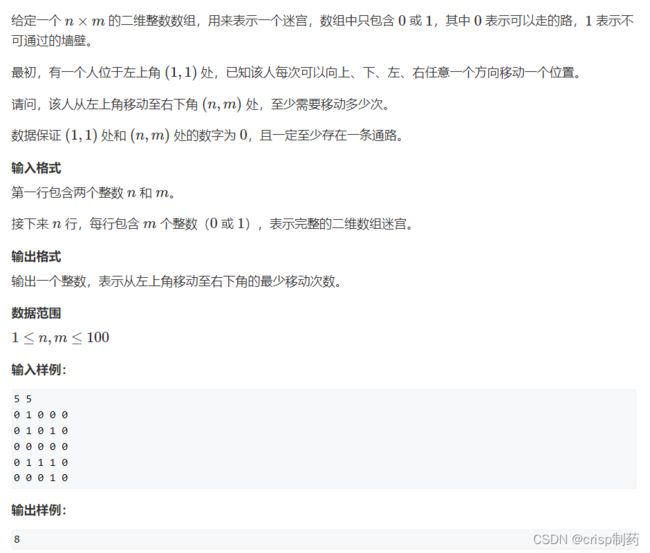
走迷宫
这题是非常基础的一道BFS的模板题,BFS通常用到队列,这里我们将初始状态放到队列里面去,从起点开始广度优先遍历地图。然后每次只添加可以走且第一次走的点,因为每次走的都是第一次走的因此最后到达终点时的距离一定是最短距离。就输出d[n-1][m-1]。
#include
#include
#include
#include
using namespace std;
typedef pair PII;//这个是stl里pair类型容器的用法,pair容器中每个容器装两个量(可自定义),first就是此容器中的第一个量,second就是第二个量
const int N = 110;
int n, m;
int g[N] [N], d[N] [N];//g数组存的是整个地图,d数组存的是每一个点到起点的距离
int bfs()
{
queue q;
memset(d, -1, sizeof d);//初始化为-1,表示这个点没有走过,=0的时候就代表它走过了
d[0][0] = 0;
q.push({0, 0});
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (q.size())
{
auto t = q.front();//取出来队头元素
q.pop();
for (int i = 0; i < 4; i ++ )
{
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//这个点在边界内,并且不能走过,第一次走过的点才是最短距离,g[x][y]=0代表可走。
{
d[x][y] = d[t.first][t.second] + 1;//从当前点走过去,则距离等于当前点的距离+1.
q.push({x, y});//把这个点放在队列中
}
}
}
return d[n - 1][m - 1];//右下 角的距离
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
cin >> g[i] [j];
cout << bfs() << endl;
return 0;
} 全球变暖
这题是非常典型的连通块问题,用dfs或bfs都可以。先说说大题思路
用二维数组a存地图,vis数组表示该点是否被访问过,遍历这个二维图形,对每个点如果是#并且没有访问过那就对它进行DFS或BFS,找他所在的联通块,寻找整个连通块,看看是否存在有陆地是上下左右都被陆地包围的点,如果有就说明该岛屿不会被完全淹没,就让flag=1
注意边界问题,以及该点是否被访问过等细节
DFS版本代码
#include
using namespace std;
const int N =1010;
char a[N][N];
int n;
int vis[N][N];
int d[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
int flag;
void dfs(int x,int y)
{
vis[x][y]=1;
if(a[x][y+1]=='#' && a[x][y-1]=='#' && a[x-1][y]=='#' && a[x+1][y]=='#')
flag=1;//如果上下左右都是陆地的话
for(int i=0;i<4;i++)
{
int nx=x+d[i][0],ny=y+d[i][1];//进行移动,如果该点还是陆地的话那就对它进行DFS
if(vis[nx][ny]==0&&a[nx][ny]=='#')
dfs(nx,ny);
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[i][j]=='#'&&vis[i][j]==0)//判断是不是陆地,且是否访问过
{
flag=0;
dfs(i,j);
if(flag==0)
ans++;//被完全淹没次数
}
cout< BFS
#include
using namespace std;
const int N =1010;
char a[N][N];
int n;
typedef pairPII;
int vis[N][N];
int flag,tmp;
void bfs(int i,int j)
{
queueq;
vis[i][j]=1;
q.push({i,j});
int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
while(q.size())
{
auto t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if (x<0||x>=n||y>=n||y<0)//判断是否出界
continue;
if(a[x][y]=='#'&&vis[x][y]==0)
{
vis[x][y]=1;
if(a[x + 1][y] == '#' && a[x - 1][y] == '#' && a[x][y + 1] == '#' && a[x][y - 1] == '#')//判断该点上下左右是否都为陆地
flag = 1;
q.push({x,y});//判断完之后把该点放入队列中
}
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[i][j]=='#'&&vis[i][j]==0)//如果是陆地且没有被访问过那就进行BFS
{
flag=0;
bfs(i,j);
if(flag==0)
ans++;
}
cout<