数据结构入门-10-AVL
文章目录
- 一、AVL的性质
-
- 1.2 平衡二叉树定义
- 二、添加需达到平衡
-
- 2.1 平衡因子
-
- 2.1.2 平衡因子的实现
- 2.2 判断该二叉树是否为平衡二叉树
- 2.3 左旋右旋
-
- 2.3.1 左旋LL右旋RR基本原理
- 2.3.2 LR RL
-
- LR
- RL
- 三、AVL中删除
一、AVL的性质
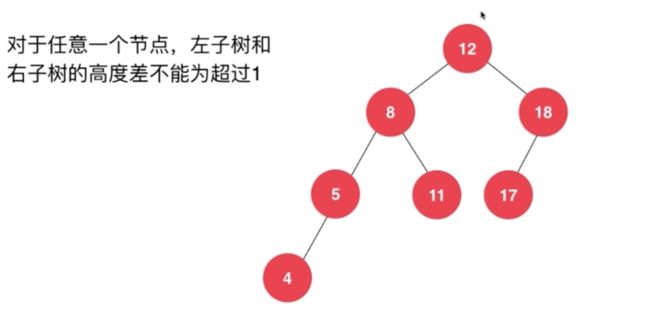
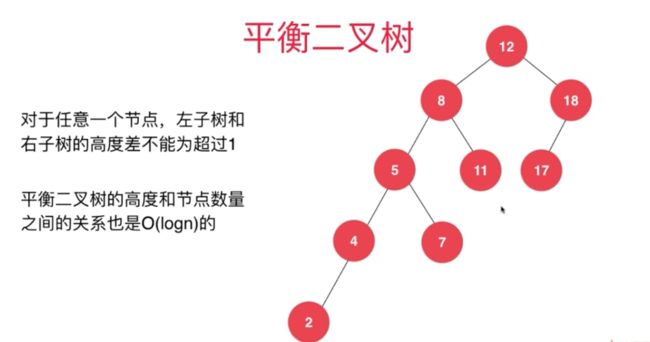
平衡二叉树
AVL树得名于它的俄罗斯发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它
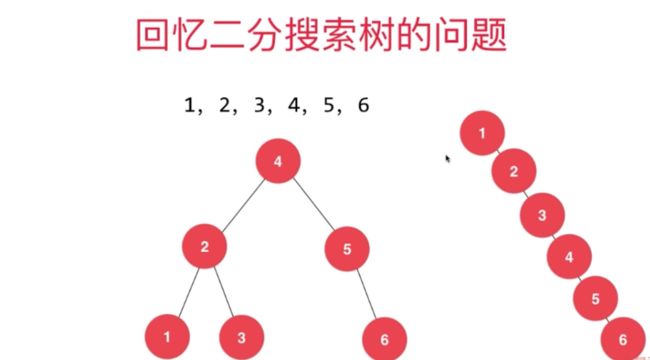
防止二分搜索树出现退化成链表的情况
1.2 平衡二叉树定义
之前讲过的 完全二叉树：差值不会超过1，缺失一定在右下侧
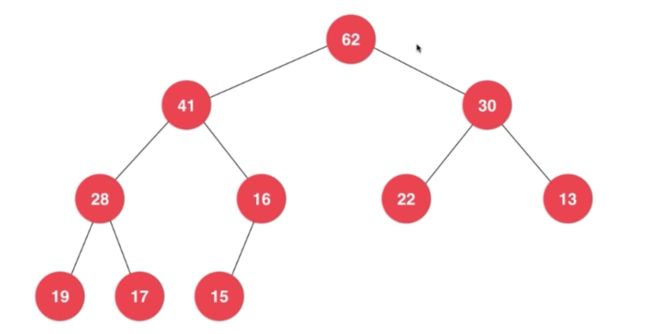
平衡二叉树：高度(左子树) - (右子树) <= 1
和完全二叉树的区别：
二、添加需达到平衡
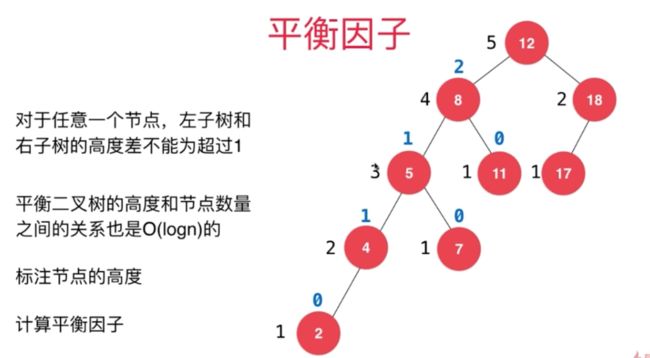
2.1 平衡因子
再次2添加带来的问题：
- 标记节点的高度
- 计算平衡因子
- 平衡因子 > 1 就需要重新整理
2.1.2 平衡因子的实现
import java.util.ArrayList;
public class AVLTree<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
public Node left, right;
public int height;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
public AVLTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 获得节点node的高度
private int getHeight(Node node){
if(node == null)
return 0;
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1)
System.out.println("unbalanced : " + balanceFactor);
return node;
}
2.2 判断该二叉树是否为平衡二叉树
// 判断该二叉树是否是一棵二分搜索树
public boolean isBST(){
ArrayList<K> keys = new ArrayList<>();
inOrder(root, keys);
for(int i = 1 ; i < keys.size() ; i ++)
if(keys.get(i - 1).compareTo(keys.get(i)) > 0)
return false;
return true;
}
//用中序遍历，查看是否是从小到大
private void inOrder(Node node, ArrayList<K> keys){
if(node == null)
return;
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
判断树是否为平衡二叉树
// 判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced(){
return isBalanced(root);
}
// 判断以Node为根的二叉树是否是一棵平衡二叉树，递归算法
private boolean isBalanced(Node node){
if(node == null)
return true;
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1)
return false;
return isBalanced(node.left) && isBalanced(node.right);
}
// 获得节点node的高度
private int getHeight(Node node){
if(node == null)
return 0;
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
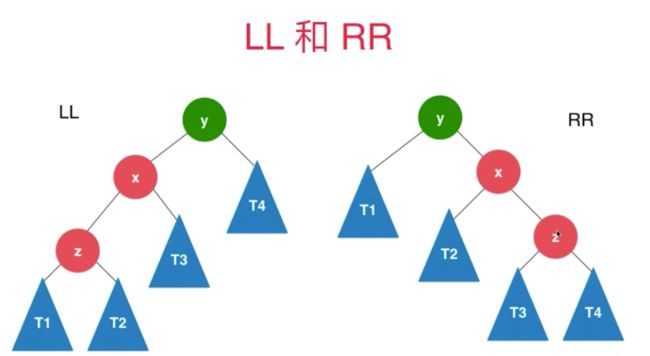
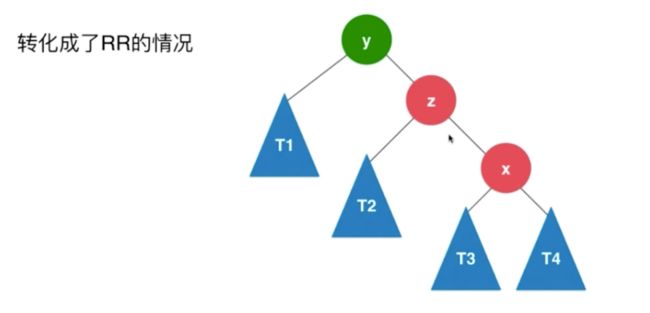
2.3 左旋右旋
2.3.1 左旋LL右旋RR基本原理
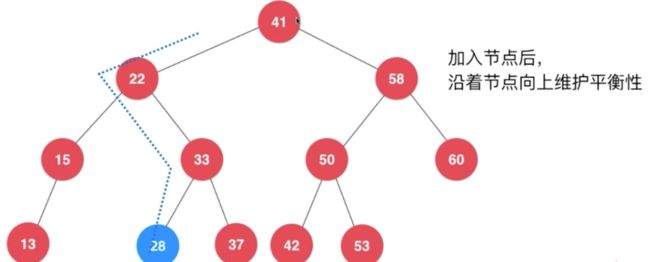
这个左旋可不能减肥
之前在BST中的add后维护
在AVL中，之前的例子 add(2)
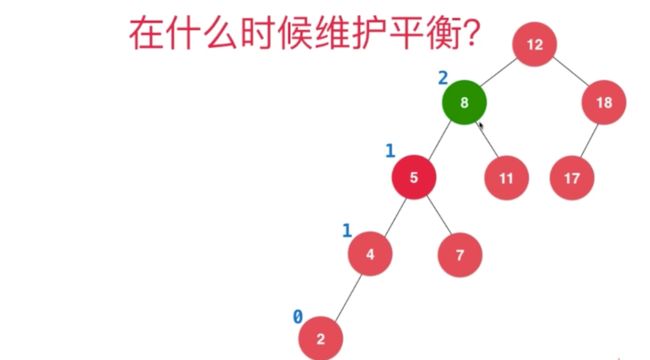
8的平衡因子2
简化刚才的例子，T1…5 为叶子 可能为空
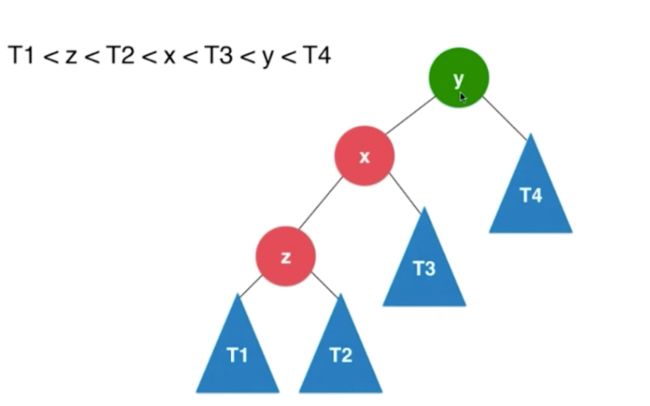
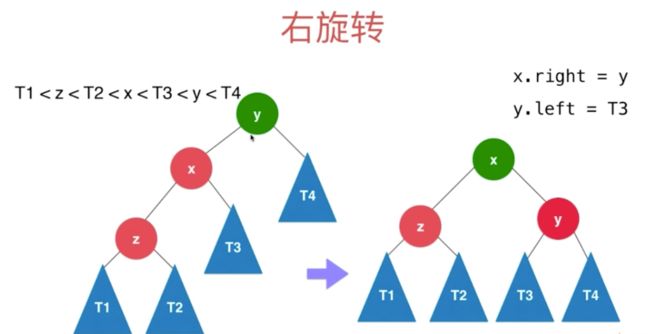
// 对节点y进行向右旋转操作，返回旋转后新的根节点x
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
左旋转类似
// 对节点y进行向左旋转操作，返回旋转后新的根节点x
// y x
// / \ / \
// T1 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T2 z T1 T2 T3 T4
// / \
// T3 T4
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
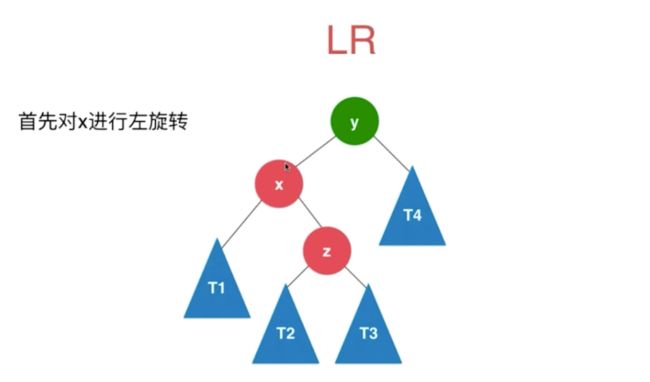
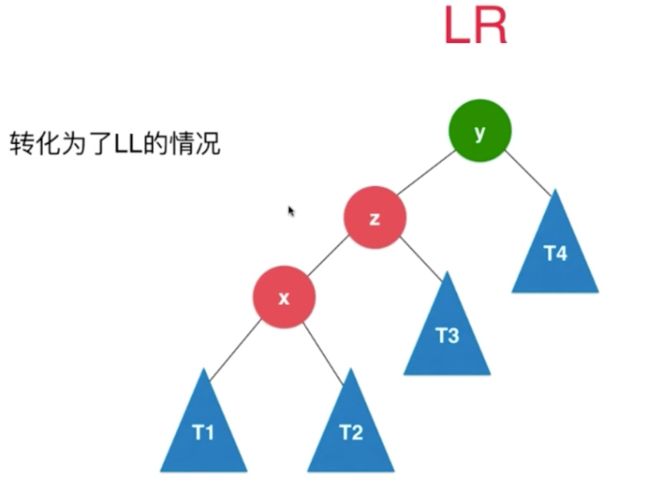
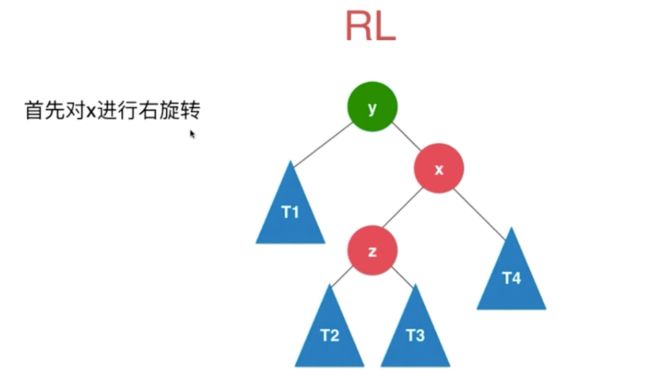
2.3.2 LR RL
当插入4 10 的时候，就不能简单的旋转了
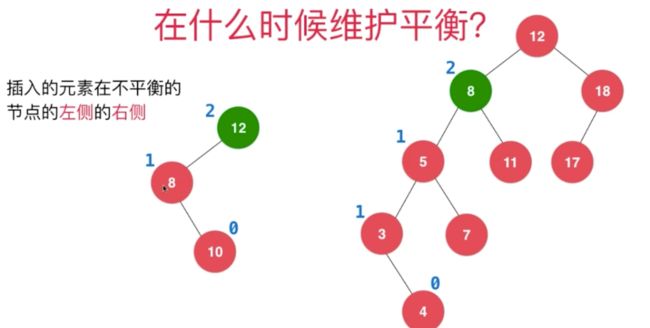
因为10 > 8 所以直接旋转还是不满足BST
例子中的是LR的情况，需要先对x做一次左旋转
LR
转换成了LL的情况
RL
转换成了RR
// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 平衡维护
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
return rightRotate(node);
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
return leftRotate(node);
//LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
//RL
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
三、AVL中删除
和添加类似