【数据结构】第二章线性表:单链表的定义、插入和删除、查找、建立
目录
2.3_1 单链表的定义
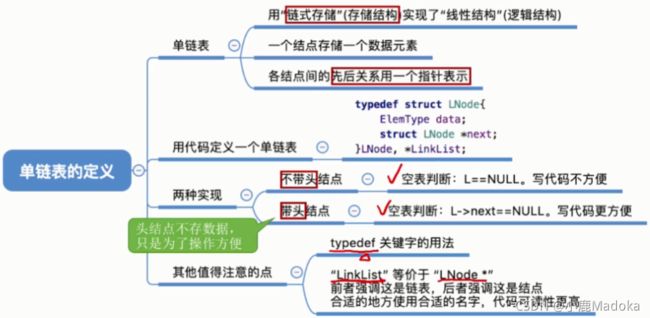
一、什么是单链表
二、用代码定义一个单链表
(1)结构体变量和结构体类型的定义
(2)不带头结点的链表
(3)带头结点的单链表
(4)头指针和头结点的理解
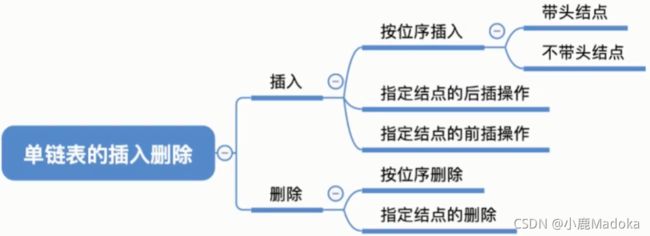
2.3_2 单链表插入和删除
一、按位序插入(带头结点)
二、按位序插入(不带头结点)
三、指定结点的后插操作
四、指定结点的前插操作
五、按位序删除(带头结点)
六、指定结点的删除
小结Tips:
2.3.2.2 单链表的查找
一、按位查找
二、按值查找
三、求单链表长度(带头结点)
2.3.2.3_4 单链表的建立
一、尾插法建立单链表
二、头插法建立单链表
2.3_1 单链表的定义
一、什么是单链表
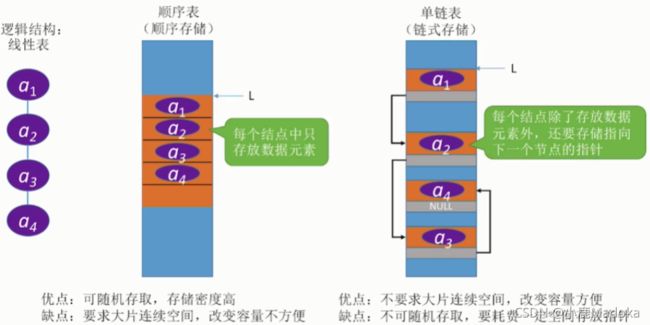
用链式存储的线性表统称为链表。
二、用代码定义一个单链表
(1)结构体变量和结构体类型的定义
首先,我们按照之前 C/C++ 中学过的语法来定义一个结构体时是这样的:
struct LNode{ // 定义单链表结点类型
ElemType data; // 数据域
struct LNode *next; // 指针域
};
// 在内存中申请一个结点所需的空间,并用指针p指向这个结点
struct LNode *p = (struct LNode *)malloc(sizeof(struct LNode));一句代码写得很长,有一个更方便的写法,引入 typedef 关键字进行数据类型重命名,把全名自定义成自己起的小名,使用起来更快捷。
typedef <数据类型> <别名>; typedef 关键字,将 struct LNode 这个结构体类型名字重新定义为 LNode 和 *LinkList(用来表示指向struct LNmde的指针);
下次想定义一个 struct LNode 结构体变量时,直接 LNode 变量名,就可以了;
初次修改代码为:
struct LNode{
ElemType data;
sruct LNode *next;
};
typedef struct LNode LNode;
// 在使用它生成新结点时的代码:
LNode *p = (LNode *)malloc(sizeof(LNode)); 参考菜鸟教程链接:结构体变量和结构体类型的定义 | 菜鸟教程
*LinkList 是结构体指针,使用结构体指针对结构成员的访问(比如做遍历输出数据域时),与结构变量对结构成员的访问在表达方式上有所不同,结构指针对结构成员的访问表示为:结构指针名 -> 结构成员(与 . 优先级有关)
增加一个结构体指针之后的代码:
struct LNode{
ElemType data;
sruct LNode *next;
};
typedef struct LNode LNode;
typedef struct Lnode *LinkList;
// 在使用它生成新结点时的代码:
// 要表示一个单链表时,只需要声明一个头指针L,指向单链表的第一个结点
LNode *L; // 声明一个指向单链表第一个结点的指针
// 或
LinkList L;
而它的效果和下面的代码是一样的,所以我们定义单链表时用如下形式,LNode * 强调“返回的是一个结点”,LinkList 强调“这是一个单链表”,两者根据不同的场景使用会使代码可读性更高。
// 单链表定义
typedef struct LNode{ // 定义单链表结点类型
ElemType data; // 每个结点存放一个数据元素
struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList; (2)不带头结点的链表
// 20220331 补充代码
// 2.3_1 单链表的定义——不带头结点的链表初始化、判空
#include
using namespace std;
# define ElemType int
typedef struct LNode{ // 定义单链表结点类型
ElemType data; // 每个结点存放一个数据元素
struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;
// 初始化一个空的单链表
bool InitList(LinkList &L){
L = NULL; // 空表,暂时还没有任何结点(防止脏数据)
return true;
}
// 判断单链表是否为空
bool Empty(LinkList L){
return (L == NULL);
}
int main(){
// 声明一个不带头结点的单链表L
LinkList L;
// 初始化
bool InitFlag = 0;
InitFlag = InitList(L);
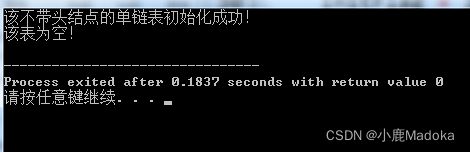
if(InitFlag) cout << "该不带头结点的单链表初始化成功!" << endl;
else cout << "该不带头结点的单链表初始化不成功。" << endl;
// 判空
bool EmptyFlag = 0;
EmptyFlag = Empty(L);
if(Empty(L)) cout << "该表为空!" << endl;
else cout << "该表不为空。" << endl;
return 0;
} (3)带头结点的单链表
// 20220401 补充代码
// 2.3_1 单链表的定义——带头结点链表的初始化、判空
#include
#include
using namespace std;
#define ElemType int
typedef struct LNode{ // 定义单链表结点类型
ElemType data; // 每个结点存放一个数据元素
struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;
// 初始化一个单链表(带头结点)
bool InitList(LinkList &L){
L = (LNode *)malloc(sizeof(LNode)); // 分配一个头结点
if(L == NULL) return false; // 内存不足,分配失败
L->next = NULL; // 头结点之后暂时还没有结点
return true;
}
// 判断单链表是否为空(带头结点)
bool Empty(LinkList L){
return (L->next == NULL);
}
int main(){
// 声明一个指向单链表的指针
LinkList L;
// 初始化单链表
bool InitFlag = 0;
InitFlag = InitList(L);
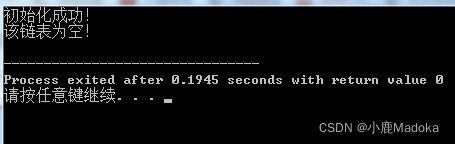
if(InitList) cout << "初始化成功!" << endl;
else cout << "初始化失败。" << endl;
// 判空
bool EmptyFlag = 0;
EmptyFlag = Empty(L);
if(EmptyFlag) cout << "该链表为空!" << endl;
else cout << "该链表不为空。" << endl;
return 0;
} (4)头指针和头结点的理解
一定要带头结点,因为:
不带头结点,写代码更麻烦,对第一个数据结点和后续数据结点的处理需要用不同的代码逻辑,对空表和非空表的处理需要用不同的代码逻辑。
Q:数据结构中的头结点、头指针、开始结点有什么区别?
头结点:链表中物理上的第一个结点;
头指针:指向物理上第一个结点的指针(存放该结点地址的变量);
开始结点:逻辑上第一个元素的结点。一般而言,如果链表没有空的头结点,则头结点就是开始结点;但是数据结构中为了简化插入删除操作,链表一般都是有空的头结点的,这样开始结点就成了事实上(物理上的)第二个结点了。
有了头结点,对在第一元素结点前插入结点和删除第一结点起操作与其它结点的操作就统一了。
头指针和头结点的区别_菜鸟的修炼-CSDN博客_头指针和头结点的区别
2.3_2 单链表插入和删除
一、按位序插入(带头结点)
ListInsert(&L, i, e) :插入操作。在表L中的第i个位置上插入元素e。
找到第i-1个结点,将新结点插入其后。
头结点可以看做“第0个”结点。
指针p从前向后遍历链表的每一个结点,指向插入位序的前一个结点;
把新结点链入链表时,先链新结点的指针域,再链前一个结点的指针域;
// 20220401 补充代码
// 2.3_2 单链表的插入和删除——带头结点的单链表的按位序插入
#include
#include
using namespace std;
#define ElemType int
typedef struct LNode{ // 单链表定义
ElemType data; // 数据域
LNode *next; // 指针域
}LNode, *LinkList;
// 初始化
bool InitList(LinkList &L){
L = (LNode *)malloc(sizeof(LNode)); // 分配一个头结点
if(L == NULL) return false; // 内存不足,分配空间失败
L->next = NULL; // 头结点之后还暂时没有结点
return true;
}
// 插入结点,在第i个位置插入元素e(带头结点)
bool ListInsert(LinkList &L, int i, ElemType e){
if(i < 1) return false; // 插入位序不能比1小
LNode *p; // 指针p指向当前扫描到的结点
int j = 0; // 当前p指向的是第几个结点(位序)
p = L; // L指向头结点,头结点是第0个结点(不存数据)
while(p != NULL && j < i-1){ // 循环找到第i-1个结点
p = p->next;
j++;
}
if(p == NULL) return false; // i值不合法
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e;
s->next = p->next; // 先连本结点指针域
p->next = s; // 再连后结点指针域
return true;
}
int main(){
// 声明一个指向单链表的指针
LinkList L;
// 初始化单链表
InitList(L);
// 插入结点
bool InsertFlag = 0;
InsertFlag = ListInsert(L, 1, 4);
if(InsertFlag) cout << "插入结点成功!" << endl;
else cout << "插入结点失败。" << endl;
// 打印该结点
cout << "第一个结点的值为:" << L->next->data << endl;
return 0;
}
时间复杂度分析:(问题规模n指表长)
平均时间复杂度:O(n)
二、按位序插入(不带头结点)
ListInsert(&L, i, e):插入操作,在表L的第i个位置上插入置顶元素e。
找到第i-1个结点,将新结点插入其后。
因为不存在“第0个”结点,因此i=1时需要特殊处理。
// 200220401 补充代码
// 2.3_2 单链表插入和删除——不带头结点的单链表的按位序插入
#include
#include
using namespace std;
#define ElemType int
typedef struct LNode{
ElemType data;
LNode *next;
}LNode, *LinkList;
// 初始化
bool InitList(LinkList &L){
L = NULL;
return true;
}
// 按位插入,在i的位序上插入结点值e
bool ListInsert(LinkList &L, int i, ElemType e){
if(i < 1) return false;
if(i == 1){ // 对插入第一个位序的结点单独判断
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e;
s->next = L; // 先链新结点的指针域
L = s; // 再为头指针赋值
return true;
}
LNode *p; // 指针p指向当前扫描到的结点
int j = 1; // 当前p指向的是第几个结点
p = L; // p指向第一个结点(注意:不是头结点)
while(p != NULL && j < i-1){ // 循环找到第i-1个结点
p = p->next;
j++;
}
if(p == NULL) return false; // i值不合法
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e;
s->next = p->next; // 先链新结点指针域
p->next = s; // 再链前一个结点指针域
return true;
}
int main(){
// 声明一个指向单链表的指针
LinkList L;
// 初始化
InitList(L);
// 插入结点
bool InsertFlag = 0;
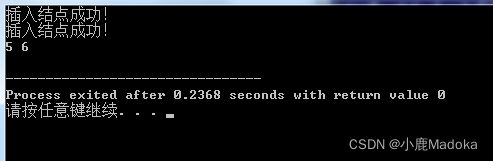
InsertFlag = ListInsert(L, 1, 5);
if(InsertFlag) cout << "插入结点成功!" << endl;
else cout << "插入结点失败。" << endl;
InsertFlag = 0;
InsertFlag = ListInsert(L, 2, 6);
if(InsertFlag) cout << "插入结点成功!" << endl;
else cout << "插入结点失败。" << endl;
// 测试
cout << L->data << " " << L->next->data << endl;
return 0;
}
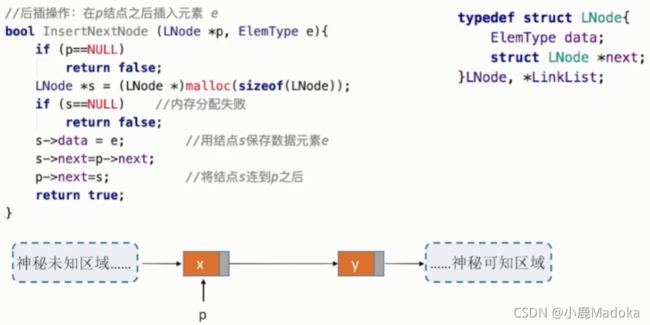
三、指定结点的后插操作
在p结点之后插入元素e
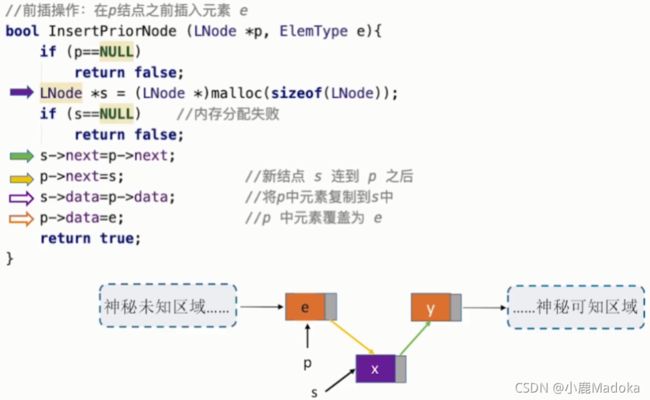
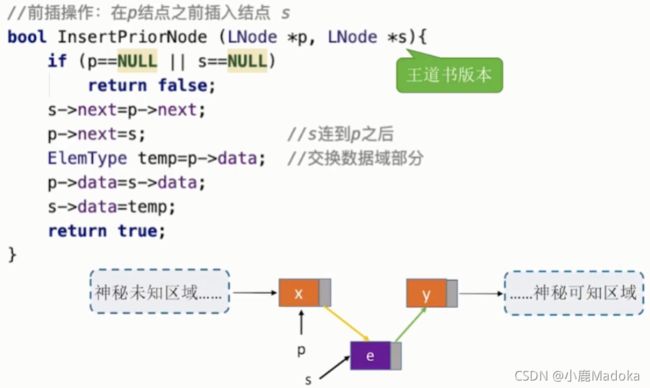
四、指定结点的前插操作
在p结点之前插入元素e
按照先找p的前一位q,在进行插入操作,时间复杂度为O(n)
可以将e结点插入p后面,然后再交换e、p的值,时间复杂度为O(1)
书中版本是传递结点:
五、按位序删除(带头结点)
ListDelete(&L, i, &e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素值。
找到第i-1个结点,将其指针指向第i+1个结点,并释放第i个结点。
最坏、平均时间复杂度:O(n)
最好时间复杂度:O(1)
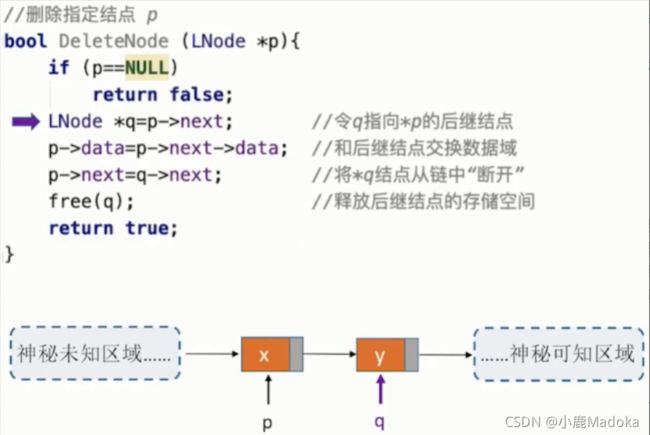
六、指定结点的删除
删除结点p,需要修改其前驱结点的next指针,但是需要查找p的前驱结点。
方法1:传入头指针,循环寻找p的前驱结点;
方法2:类似于结点前插的实现。删除结点p,那就把它的后继结点q的数据和它的数据互相交换,再将q(p的后继结点)的指针域赋给p的指针域;
时间复杂度O(1)
如果p是链表中最后一个结点,就完成不了删除操作了,只能从表头开始依次寻找p的前驱,时间复杂度O(n);
单链表的局限性:无法逆向检索,有时候操作起来并不方便。
小结Tips:
- 这些代码都要会写,都重要
- 打牢基础,慢慢加速
- 体会到带头结点、不带头结点的代码区别
- 体会“封装”的好处(如下图所示,可以把“寻找位序i-1的结点”,“指定结点的后插操作”这两个功能封装起来,用的时候更加方便)
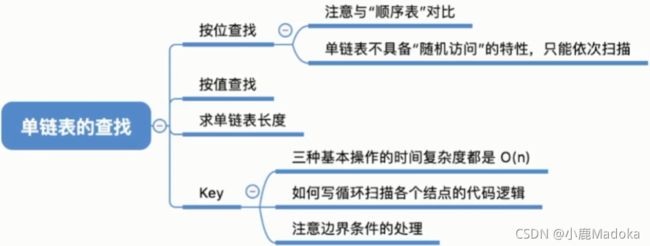
2.3.2.2 单链表的查找
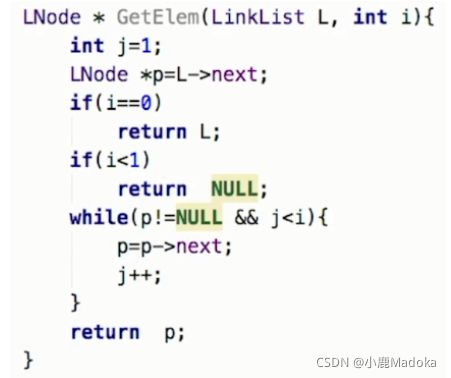
一、按位查找
之前学到的插入删除结点操作中,已经用到过按位查找了。
按位查找平均时间复杂度:O(n)
课本中如下代码是另一种写法,给j赋1,单独判断查找元素是第一个结点的情况。
因为别的基本操作几乎都要用到按位查找,所以我们可以把这个方法封装起来;
封装的好处:避免重复代码,简洁、易维护
二、按值查找
*!=操作符只能用于int类型的判断,不能用于struct的比较判断,如何比较struct结构体是否相等呢?将结构体中成员分别进行比较,或者进行运算符重载。
时间复杂度:O(n)
三、求单链表长度(带头结点)
// 求单链表的长度(带头结点)
int length(LinkList L){
int len = 0; //统计表长
LNode *p = L; // 一开始p指向头结点
while(p->next != NULL){ // 判断当前结点的指针域是否为空(不为空则代表有后继结点)
p = p->next;
len++;
}
return len;
} 为什么传来的参数值是 LinkList L 呢?——因为头结点已经在建立的时候就确定了,不用修改了。也就是说,如果头指针L改变了,我们就传参时使用引用 变为 LinkList* L;像按位插入、删除等等不改变头结点,就不需要加引用&。
主函数内的调用代码为:
// 求表长
int len = length(L2);
printf("当前单链表表长为:%d", len); 实参L2为 LinkList L2;时的链表指针;
2.3.2.3_4 单链表的建立
本节讨论带头结点的单链表建立:
Step1:初始化一个单链表;
Step2:每次取一个数据元素,插入到表尾/表头;
头插法、尾插法:核心就是初始化操作,指定结点的后插操作。
一、尾插法建立单链表
如上使用按位序插入新结点的方式,while循环每次都从头开始之后的遍历,时间复杂度为O(n的平方);
为了解决时间每次都要while循环来寻找新插入结点位置带来的时间复杂度过高问题,可设置一个表尾指针,如下方式,时间复杂度为O(n)。
// 202110026 单链表带头结点_尾插法建立
#include
#include // C输入输出
#include // malloc
using namespace std;
typedef int ElemType; // 单链表结点数据域存放int整型变量
// 单链表定义
typedef struct LNode{ // 定义单链表结点类型
ElemType data; // 每个结点存放一个数据元素
struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;
/*
强调这是一个单链表使用LinkList;
强调这是一个结点使用LNode *;
*/
// 尾插法建立单链表(带头结点)
LinkList List_TailInsert(LinkList &L){ // 正向建立单链表
int x; // 设elemType为整型
L = (LinkList)malloc(sizeof(LNode)); // 建立头结点(初始化空表)
LNode *s, *r = L; // r为表尾指针
scanf("%d", &x); // 输入结点的的值
while(x != 9999){ // 输入9999表示结束
// 在最后一个结点r之后插入新结点s
s = (LNode *)malloc(sizeof(LNode));
s->data = x; // 为新结点数据域赋值
r->next = s; // 将新结点链入链表
r = s; // r指向新的表尾结点(永远保持r指向最后一个结点)
scanf("%d", &x);
}
r->next = NULL; // 尾结点指针置空
return L;
}
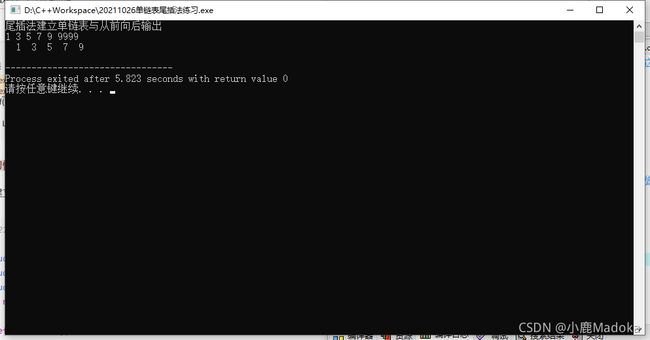
int main(){
// 尾插法建立单链表与从前向后输出
printf("尾插法建立单链表与从前向后输出\n");
// 声明一个单链表
LinkList L2;
// 尾插法建立单向链表
List_TailInsert(L2);
// 从前向后遍历输出数据
LNode *s2 = L2->next; // s结点从第一个结点开始遍历
while(s2 != NULL){
printf("%3d", s2->data);
s2 = s2->next;
}
free(s2);
printf("\n");
return 0;
} 输入数据:1 3 5 7 9 9999
二、头插法建立单链表
头插法建立单链表就是在头结点后不断插入新的结点,一定要记得头结点的指针域要初始化为NULL。
为什么尾插法不用把头结点指针域设为NULL呢?
尾插法在最后给尾指针r的next域置NULL效果是一样的。
头插法的头结点指针域不设为NULL会怎样呢?
可能会有脏数据,空链表时也会有第一个结点,存了脏数据。
养成好习惯,只要实现初始化单链表,都先把头指针指向NULL。
头插法建立单链表应用场景:链表的逆置
以下代码的初始化链表 InitList2 并未用到
// 202110026 单链表带头结点_头插法建立
#include
#include // C输入输出
#include // malloc
using namespace std;
typedef int ElemType; // 单链表结点数据域存放int整型变量
// 单链表定义
typedef struct LNode{ // 定义单链表结点类型
ElemType data; // 每个结点存放一个数据元素
struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;
/*
强调这是一个单链表使用LinkList;
强调这是一个结点使用LNode *;
*/
// 初始化一个单链表(带头结点)
bool InitList2(LinkList &L){
L = (LNode *)malloc(sizeof(LNode)); // 分配一个头结点
if(L == NULL){ // 内存不足,分配失败
return false;
}
L->next = NULL; // 头结点之后还暂时没有结点
return true;
}
// 头插法建立单链表(带头结点)
LinkList List_HeadInsert(LinkList &L){ // 逆向建立单链表
LNode *s;
int x;
L = (LinkList)malloc(sizeof(LNode)); // 创建头结点
L->next = NULL; // 初始为空链表
scanf("%d", &x); // 输入结点的值
while(x != 9999){ // 输入9999表示结束
s = (LNode *)malloc(sizeof(LNode)); // 创建新结点
s->data = x; // 为新结点数据域赋值
s->next = L->next; // 为新结点指针域赋值
L->next = s; // 将新结点插入表中
scanf("%d", &x);
}
return L;
}
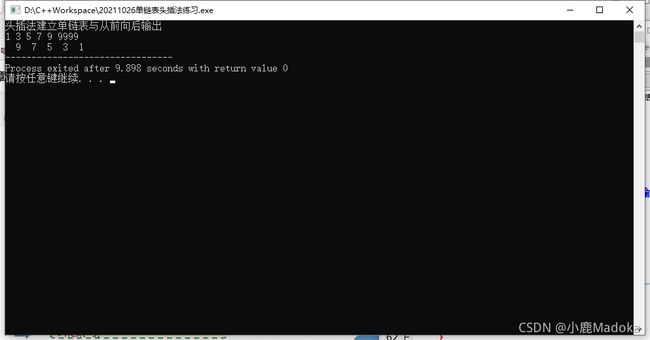
int main(){
// 头插法建立单链表与从前向后输出
printf("头插法建立单链表与从前向后输出\n");
// 初始化一个带头结点的单链表
LinkList L1;
InitList2(L1);
// 头插法建立单链表
List_HeadInsert(L1);
// 从前向后遍历输出数据
LNode *s = L1->next; // s结点从第一个结点开始遍历
while(s != NULL){
printf("%3d", s->data);
s = s->next;
}
free(s);
return 0;
}
输入数据:1 3 5 7 9 9999
输出数据:9 7 5 3 1