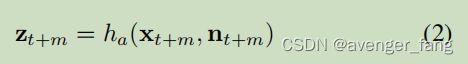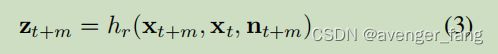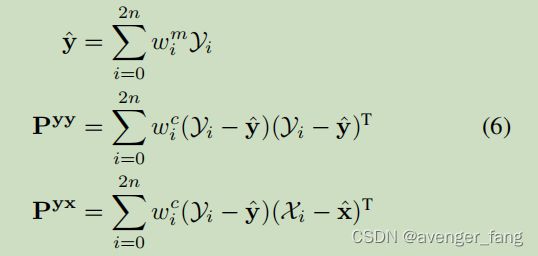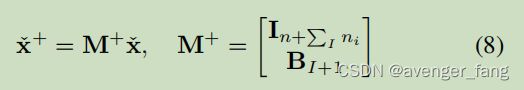2014ICRA 宾大沈邵杰 《Multi-Sensor Fusion for Robust Autonomous Flight in Indoor andOutdoor Environments》

论文名： 

Multi-Sensor Fusion for Robust Autonomous Flight in Indoor and Outdoor Environments with a Rotorcraft MAV

Abstract

        我们提出了一种模块化和可扩展的方法来集成来自多个异构传感器的噪声测量，这些传感器在不同和不同的时间间隔内产生绝对或相对观测，并为自动飞行提供平滑和全局一致的实时位置估计。我们描述了一个新的1.9 kg MAV平台的算法和软件架构的发展，该平台配备了IMU、激光扫描仪、立体相机、压力高度计、磁强计和GPS接收器，其中状态估计和控制在英特尔NUC第三代i3处理器上执行。我们在大规模的室内-室外自主空中导航实验中说明了我们的框架的鲁棒性性，这些实验包括在进出建筑物时，以平均速度1.5m/s穿越超过440米，风速约为每小时10英里。 

I. INTRODUCTION  

        旋翼微型飞行器（MAVs）由于其体积小尺寸、优越的机动性和悬停能力，是在有限的室内和室外环境中监视和搜索和救援的理想平台。在这类任务中，MAV必须能够自动飞行，以最小化操作员的工作量。鲁棒状态估计对自主飞行至关重要，特别是因为mav固有的快速动态。由于成本和有效载荷的限制，大多数mav都配备了低成本的本体感觉传感器（如MEMS-imu），无法进行长期的状态估计。因此，外部感受传感器，如GPS、照相机和激光扫描仪，通常与本体感受传感器融合，以提高估计精度。

        除了发展完善的基于GPS的导航技术[1,2]。最近有文献表明，在使用激光扫描仪[3,4]、单目相机[5,6]、立体相机[7,8]和RGB-D传感器[9]在被GPS无信号的环境下对自动飞行进行稳健状态估计。然而，所有这些方法都依赖于单一的外部感受感知模式，这种模式只在特定的环境条件下发挥作用。例如，基于激光的方法需要结构化的环境，基于视觉的方法需要足够的照明和功能，而GPS只在户外工作。

        这使得它们在涉及户内外过渡的大规模环境中容易失败，其中环境可以改变巨大。很明显，在这种情况下，可以使用GPS、相机和激光的多个测量，所有这些测量的融合提高了估计器的精度和鲁棒性。然而，在实践中，这些额外的信息要么被忽略，或者作为传感器套件[10]之间的切换来处理。

        这项工作的主要目标是开发一个模块化和可扩展的方法来融合噪声测量从多个异构传感器产生绝对或相对观察在不同和不同的时间间隔，并提供平滑和全局一致的估计自主飞行的实时位置。第一个关键的贡献，是我们工作的核心，是一个有原则的方法，建立在[11]的基础上，通过增加车辆状态和以前的状态的副本来融合相对测量，创建一个增强的状态向量，使用过滤框架获得和保持一致的估计。第二个重要的贡献是我们的无迹卡尔曼滤波（UKF）公式，其中的传播和更新步骤规避了由于增广状态的协方差矩阵的半正定所导致的困难。最后，我们用一个新的实验平台（图1）来演示结果，以说明我们的框架在大规模的室内外自主空中导航实验中的鲁棒性，该实验包括平均速度超过440米，风速约为每小时10英里。

        接下来，我们将介绍我们的工作所基于的先前的工作。在第三节中，我们在第四节中介绍基于UKF的传感器融合方案的关键贡献之前，我们概述了建模框架。我们将第六节中对实验平台的描述和实验结果结合在一起。

II. PREVIOUS WORK

        我们感兴趣的是应用基于常数计算复杂度滤波的方法，如卡尔曼滤波器的非线性变量，来融合所有可用的传感器信息。我们强调，尽管基于SLAM的多传感器融合方法[12,13]产生最优结果，但对于自动控制的实时状态反馈，它们的计算成本是昂贵的。 

        虽然在递归滤波公式中可以直接融合多个绝对测量值，如GPS、压力/激光高度计，但从激光或视觉里程计获得的多个相对测量值的融合更复杂。通常会将相对测量值与先前的状态估计值累积起来，并将它们融合为伪绝对测量值[5,14]。然而，这种融合是次优的，因为所得到的全局位置和偏航协方差与实际估计误差相比是不一致的小量。这违反了可观测性性质[6]，这表明这样的全局量实际上是不可观测的。因此，我们开发了基于状态增强技术[11]的方法，以适当地考虑在应用来自多个传感器的多个相对测量时的状态不确定性。

        我们的目标是开发一个模块化框架，允许简单地添加和去除传感器的最小编码和数学推导。我们注意到，在流行的基于EKF的公式[5,8]中，雅可比矩阵的计算对于复杂系统是有问题的。因此，我们采用了一个松散耦合的，无导数的无迹卡尔曼滤波器（UKF）框架[1]。从EKF切换到UKF带来了几个挑战，这将在Sect4-A中详细介绍和解决。四[15]与我们的工作类似。然而，[15]中基于EKF的估计器不支持多重相对测量值的融合。

III. MULTI-SENSOR SYSTEM MODEL

        我们将世界坐标系和body坐标系中的向量分别定义为(w)和(b)。为了简洁起见，我们假设所有的板载传感器都经过校准并连接到车身坐标系上。MAV的主要状态被定义为：

         上式P为位置，角度使用欧拉角表示(注：用基于四元数的旋转表示[8,15]表示滤波器很简单，我们在第IV节中提出了简洁表示的直接公式)，它们都是基于世界坐标系的， pdot 为基于body坐标系的3D速度。由此可以得到一个表示一个向量从body坐标系到世界坐标系的旋转的矩阵Rwb。ba和bω分别是加速度计和陀螺仪的偏置，都在body坐标系中表示。bwz建模了世界坐标系内激光测距仪或压力高度计的偏差。

        我们考虑了一个基于imu的状态传播模型：

         其中u是来自body坐标系中IMU的线性加速度和角速度的测量值。vt∼N(0,Dt)∈Rm是过程噪声。va和vω表示与陀螺仪和加速度计相关的附加噪声。vba、vbω、vbz建模为陀螺仪、加速度计和高度计偏置的高斯随机游动。函数f是连续时间动力学方程[6]的一个离散版本。

        外感受传感器通常用于纠正状态传播中的误差。在[11]之后，我们将测量值看作是绝对的或相对的，这取决于底层传感器的性质。我们允许任意数量的绝对或相对测量模型。

A. Absolute Measurements

 所有绝对测量值都可以以以下形式进行建模：

 其中，nt+m∼N(0，Qt)∈Rp是可以相加或不加的测量噪声。ha(·)通常是一个非线性函数。绝对测量值将当前状态与传感器输出连接起来。例子见Sect. V-B。

B. Relative Measurements

相对测量值将当前和过去状态与传感器输出连接起来，可以写为： 

        该公式准确地模拟了类里程计算法的性质((Sect. V-C and Sect. V-D))，作为里程计测量状态的两个时间瞬间之间的增量变化。我们还注意到，为了避免时间漂移，大多数最先进的激光/视觉里程计算法都是基于关键帧的。因此，我们允许多个未来的测量（m∈M，|M| > 1）对应于相同的过去状态Xt。

IV. UKF-BASED MULTI-SENSOR FUSION

        我们希望设计一个模块化的传感器融合滤波器，易于扩展，即使是没有经验的用户。这意味着添加/删除传感器的编码量和数学偏差应该是最小的。流行的基于EKF的滤波器框架的一个缺点是需要计算雅可比矩阵，这对于一个复杂的MAV系统来说是困难和耗时的。因此，我们采用了基于无导数的UKF的方法[1]。UKF的关键是通过西格玛点的传播，通过非线性函数近似化高斯随机向量的传播。设x∼N(ˆx,Pxx)∈Rn，并考虑非线性函数：

 g为非线性函数，上面的X称为西格玛点。为UKF参数。

是平方根协方差矩阵的第i列，通常通过Cholesky分解计算。和X被称为西格玛点。随机向量y的均值、协方差，以及x和y之间的交叉点方差，可以近似为：

 其中，是对西格玛点的权重。这种无迹变换可以用于跟踪状态传播和度量更新中的协方差，从而避免了基于雅可比矩阵的协方差近似的需要。

A. State Augmentation for Multiple Relative Measurements

         由于相对测量同时依赖于当前和过去的状态，这违反了卡尔曼滤波器中的基本假设(一阶马尔可夫假设)，即测量应该只依赖于当前状态。处理这个问题的一种方法是通过状态增强[11]，即在滤波器中维护过去状态的副本。在这里，我们提出了一个扩展的[11]来处理任意数量的相对测量值模型，并有可能使多个测量值对应于相同的增广状态。我们的通用滤波器框架允许方便的设置，并便于添加和删除绝对和相对的测量模型。

        请注意，一个测量可能不会影响状态x中的所有成分。例如，视觉里程计只影响6-DOF姿态，而不影响速度v或偏差项bias。我们将第i个增广状态定义为，。是x的任意子集。我们定义了一个大小为×n的二进制选择矩阵，使得。考虑一个时刻，在滤波器中有一个增广状态，以及协方差：

 添加一个新的增强状态xI+1可以通过以下完成：

 同样，对一个增广状态xj的去除方法为：

 其中和。更新后的增强状态协方差为：

         在类里程计测量模型中，关键帧的变化仅仅是删除一个增广状态xi，然后添加具有相同Bi的另一个增广状态。由于我们允许多个相对测量对应于相同的增广状态，与[11]相比，增广状态不会在测量更新后被删除(Sect. IV-D)。

        这个状态增强公式在EKF设置中工作得很好，但是，当我们试图将其应用到UKF时，它带来了问题。因为添加一个新的增强状态(8)本质上是主状态的一个副本。由此得到的协方差矩阵ˇP+将不会是正定的，并且对于状态传播的Cholesky分解(5)将会失败（非唯一的）。我们现在希望有一些类似于EKF的雅可比矩阵的东西，但不需要显式地计算雅可比矩阵。

B. Jacobians for UKF

         在[16]中，作者提出了一种新的解释，即UKF为线性回归卡尔曼滤波器（LRKF）。在LRKF中，我们寻求找到非线性函数公式(4)的最优线性近似y= Ax +b+e,公式(4)由加权离散(公式(6)的西格玛点)的表征的分布N()。目标函数是找到最小化线性化误差e的回归矩阵A和向量b：

 如[16]所示，最优线性回归方法为：

 (9)中的线性回归矩阵A作为非线性函数(4)的线性近似。它类似于EKF公式中的雅可比矩阵。因此，UKF中的传播和更新步骤可以以与EKF类似的方式执行。

未完待续。。。