强化学习之入门笔记（二）

强化学习

一、Qlearning算法

Qlearning

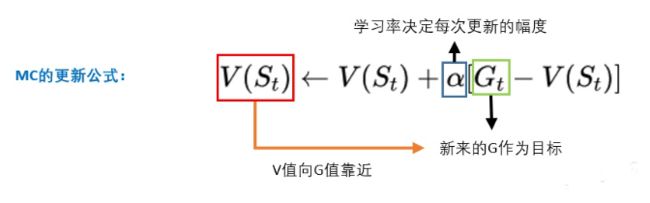
使用TD(0)预估状态价值：

图解：

但大家可能会说，TD能够用在V值，那能不能用在计算Q值上呢？答案是肯定的。

TD之于Q值估算

我们现在用上TD的思路。 我们在S_t，智能体Agent根据策略pi，选择动作A_t，进入S_t+1状态，并获得奖励R

V(S_t+1)的意义是，在S_t+1到最终状态获得的奖励期望值。 Q(S_t,A_t)的意义是，在Q(S_t,A_t)到最终状态获得的奖励期望值。 所以我们可以把V(S_t+1)看成是下山途中的一个路牌，这个路牌告诉我们下山到底还有多远，然后加上R这一段路，就知道Q(S_t,A_t)离山脚有多长的路

麻烦来了

但在实际操作的时候，会有一个问题。 在这里我们要估算两个东西，一个是V值，一个是Q值。

人们想出的办法就是，用下一个动作的Q值，代替V值。

因为从状态S_t+1到动作A_t+1之间没有奖励反馈，所以我们直接用A_t+1的Q价值，代替S_t+1的V价值。 这样不就是可以了吗?

关键是：马可洛夫链不是链，是树

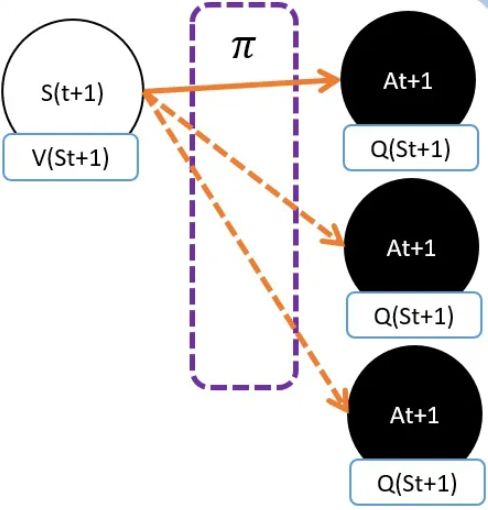
在S_t+1下，可能有很多动作A_t+1。不同动作的Q值自然是不同的。 所以Q(S_t+1,A_t+1)并不能等价于V(S_t+1)

虽然不相等，但不代表不能用其中一个来代表V(S_t+1)。人们认为有个可能的动作产生的Q值能够一定程度代表V(S_t+1)

1. 在相同策略下产生的动作A_t+1。这就是SARSA
2. 选择能够产生最大Q值的动作A_t+1。这就是Qlearning

SARSA

为什么SARSA用相同策略下产生的动作A_t+1是合理的？答案很简单，它管用

$$SARSA:Q(S,A)\leftarrow Q(S,A)+\alpha [R+\gamma Q(S^{\prime },A^{\prime })-Q(S,A)]$$
这里的A_t+1是在同一策略产生的。也就是说,S_t选A_t的策略和S_t+1选A_t+1是同一个策略。这也是SARSA和Qlearning的唯一区别

Qlearning

Qlearning能够产生最大Q值的动作A_t+1的Q值作为V(S_t+1)的替代

我们要寻找的是能够获得最多奖励的动作，Q值就代表我们能够获得今后奖励的期望值
$$\begin{gathered} Qlearning:Q(S,A)\leftarrow Q(S,A)+\alpha [R+\gamma ma{x}_{a}Q(S^{\prime },a)-Q(S,A)] \\ SARSA:Q(S,A)\leftarrow Q(S,A)+\alpha [R+\gamma Q(S^{\prime },A^{\prime })-Q(S,A)] \end{gathered}$$

• Qlearning和SARSA都是基于TD(0)的，我们用TD(0)估算状态的V值。而Qlearning和SARSA估算的是动作的Q值。
• Qlearning和SARSA的核心原理，是用下一个状态S_t+1的V值，估算Q值
• 既要估算Q值，又要估算V值会显得比较麻烦，所以我们用下一状态下的某一个动作的Q值，来代表S_t+1的V值
• Qlearning和SARSA唯一的不同，就是用什么动作的Q值替代S_t+1的V值
  • SARSA 选择的是在S_t同一个策略产生的动作
  • Qlearning 选择的是能够产生最大的Q值的动作

二、深度强化学习

为什么深度强化学习这么强，是因为深度强化学习增加了一个很强的武器——深度神经网络

函数其实也很简单，就是描述两个东西的对应关系。F(x) = y , 描述的就是x和y之间的关系。

以前的函数，需要我们去精心设计的，要设计，就要描述其中的关系。但有些东西我们明明知道他们有关系，但又不好描述清楚

例如，手写数字识别，一个正常人写的数字8，我们人类都能认出来。但我们却描述不出来，我们知道是两个圈是8，但有些人的圈明明不闭合，我们也认得出是8…

但深度神经网络这个工具就能自己学会这些关系，它是怎样做的呢？

我们要学习一个神奇函数Maigic()，辨别手写数字，也就是输入一张8的图，输出这个数字是什么

1. 我们先设一个Magic’(X)，其中的X就是输入的图片；
2. 计算结果是各个数字的概率，这个判断一开始通常都是错的，但没关系，我们会慢慢纠正它。
3. 纠正就需要有一个目标，没有目标就没有对错了。这里的目标是我们人类给他们标注的，告诉Magic’：这玩意儿是数字8
4. 目标和现实的输出总是有一段距离的，这段距离我们称为损失(loss).
5. 我们调整我们Magic’函数的参数，让损失最小化。也就是说，离目标越来越近。

最后你就发现Magci’函数的功能离我们心目中要找的Magci函数越来越近。

想要进一步了解深度神经网络，请参考文章：一篇文章入门pytorch和深度学习

三、DQN

Deep network + Qlearning = DQN

Qleanrning有一个问题：只能解决格子类型离散型状态问题，对连续型状态束手无策

在Qlearning中，我们有一个Qtable，记录着在每一个状态下，各个动作的Q值

Qtable的作用是当我们输入状态S，我们通过查表返回能够获得最大Q值的动作A，也就是我们需要找一个S-A的对应关系

这种方式很适合格子游戏，因为格子游戏中的每一个格子就是一个状态，但在现实生活中，很多状态并不是离散而是连续的

我们刚才说了，Qtable的作用就是找一个S-A的对应关系，所以我们就可以用一个函数F表示，我们有F(S)=A，这样我们就不用查表了，而且还有一个好处，函数允许连续状态的表示

这时，我们的深度神经网络就可以派上用场了，我们可以将神经网络看成一个万能的函数。这个万能函数接收输入一个状态S，它能告诉我，每个动作的Q值是怎样的

把Qtable三维可视化，就会得到这样一个图：

图中每根柱子的高度，表示状态S下，选择动作A的Q值

现在我们用函数来表示，相当于我们要扭曲一条曲线，这条曲线穿过了离散状态下的所有点

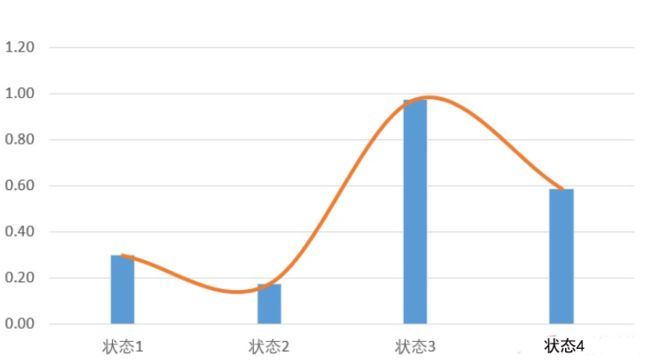
我们从二维的角度再看一下：

所以现在我们不但可以取状态3和状态4，我们还可以取状态3.5的Q值

现在我们就清楚了，其实Qlearning和DQN并没有根本的区别，只是DQN使用神经网络，也就是一个函数替代了原来的Qtable而已

神经网络的目标

神经网络需要解决一个目标，就是更新目标如何设置

在手写数字识别等有监督学习的数据集中，有标签好的数据，也就是我们的目标是很明确的。那么在DQN中，我们的目标是什么呢？

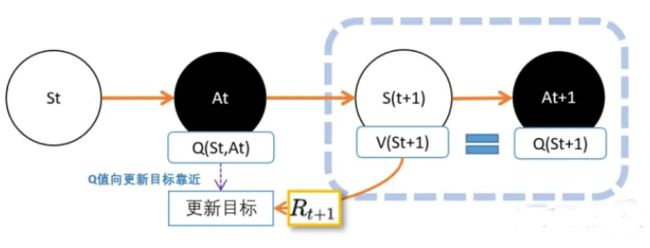
在Qlearning中，我们用下一个状态S_t+1的最大Q值替代S_t+1的V值。V(S_t+1)加上状态转移产生的奖励R，就是Q(S,a)的更新目标

我们来看下图：

假设我们需要更新当前状态S_t下的某动作A的Q值Q(S,A)，我们可以这样做

1. 执行A，往前一步，到达S_t+1
2. 把S_t+1输入Q网络，计算S_t+1下所有动作的Q值
3. 获得最大的Q值加上奖励R作为更新目标
4. 计算损失
   • Q(S,A)相当于有监督学习中的logits
   • maxQ(S_t+1)+R相当于监督学习中的labels
   • 用mse函数，得出两者的loss
5. 用loss更新Q网络

也就是，我们用Q网络估算出来的两个相邻状态的Q值，他们之间的距离，就是一个r的距离
$$DQN更新：Q(S,A)\leftarrow Q(S,A)+\alpha [R+\gamma ma{x}_{a}Q(S^{\prime },a)-Q(S,A)]$$

1. 其实DQN就是Qlearning扔掉Qtable，换上深度神经网络
2. 我们知道，解决连续型问题，如果表格不能表示，就用函数，而最好的函数就是深度神经网络
3. 和有监督学习不同，深度强化学习中，我们需要自己找更新目标。通常在马尔科夫链体系下，两个相邻状态之间的奖励R能够用来求loss

四、Policy Gradient

学到这里，我们先回顾一下，我们是怎样从0到DQN的

一开始，我们对这个世界一无所知。我们发现我们每走一步，都有一个reward，我们希望我们能够获得更多的reward，所以我们在每个状态或者动作都做上记录，希望统计一下，从这个state出发，我能获得多少奖励，这样我们就可以知道我们应该走哪条路。

于是，我们从动态规划到蒙地卡罗，到TD到Qleaning再到DQN，一路为计算Q值和V值绞尽脑汁。但大家有没有发现，我们可能走上一个固定的思维，就是我们的学习，一定要算Q值和V值。

但算Q值和V值并不是我们最终目的呀，我们要找一个策略，能获得最多的奖励。我们可以抛弃掉Q值和V值么？

答案是，可以，策略梯度(Policy Gradient)算法就是这样以一个算法。

策略梯度(Policy Gradient)

如果说DQN是一个TD+神经网络的算法，那么PG是一个蒙地卡罗+神经网络的算法

在神经网络出现之前，当我们遇到非常复杂的情况时，我们很难描述，我们遇到每一种状态应该如何应对

但现在我们有了神经网络这么强大的武器，我们就可以用一个magic函数直接代替我们想要努力描述的规则

我们用pi表示策略，也就是动作的分布。那么我们期望有这么一个magic函数，当我输入state的时候，他能输出pi，告诉智能体这个状态，应该如何应对：pi = magic(state)

如果智能体的动作是对的，那么就让这个动作获得更多被选择的几率；相反，如果这个动作是错的，那么这个动作被选择的几率将会减少

我们先来复习一下蒙地卡罗

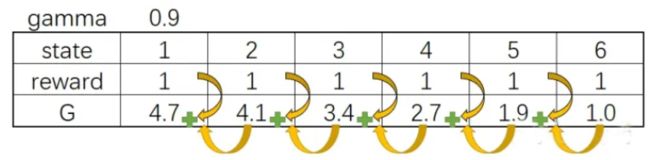
我们从某个state出发，然后一直走，直到最终状态。然后我们从最终状态原路返回，对每个状态评估G值

所以G值能够表示在策略pi下，智能体选择的这条路径的好坏

直观感受PG算法

我们先用数字，直观感受一下PG算法

从某个state出发，可以采取三个动作

假设当前智能体对这一无所知，那么，可能采取平均策略 0 = [33%,33%,33%]

智能体出发，选择动作A，到达最终状态后开始回溯，计算得到 G = 1

我们可以更新策略，因为该路径选择了A而产生的，并获得G = 1；因此我们要更新策略：让A的概率提升，相对地，BC的概率就会降低。 计算得新策略为： 1 = [50%,25%,25%]

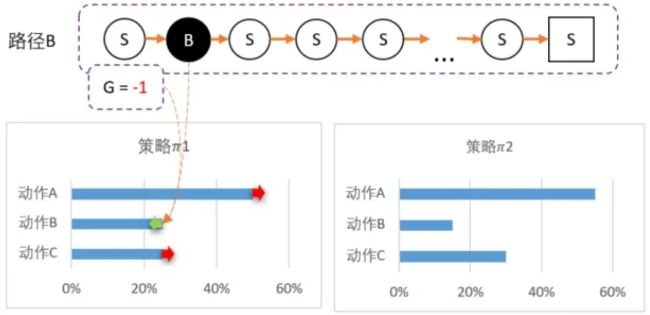
虽然B概率比较低，但仍然有可能被选中，第二轮刚好选中B

智能体选择了B，到达最终状态后回溯，计算得到 G = -1

所以我们对B动作的评价比较低，并且希望以后会少点选择B，因此我们要降低B选择的概率，而相对地，AC的选择将会提高

计算得新策略为： 2 = [55%,15%,30%]

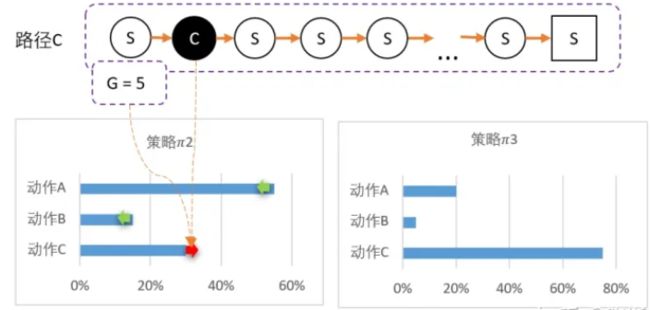
最后随机到C，回溯计算后，计算得G = 5

C比A还要多得多。因此这一次更新，C的概率需要大幅提升，相对地，AB概率降低，3 = [20%,5%,75%]

当然，以上的例子数值上是不严谨的和精确的

PG的基本思想：直接用神经网络magic(s)=a

PG用的是MC的G值来更新网络，也就是说，PG会让智能体一直走到最后，然后通过回溯计算G值

于是得到S - A - G 的数据，这里的G就是对于状态S，选择了A的评分

• 如果G值正数，那么表明选择A是正确的，我们希望神经网络输出A的概率增加(鼓励)
• 如果G是负数，那么证明这个选择不正确，我们希望神经网络输出A概率减少(惩罚)
• 而G值的大小，就相当于鼓励和惩罚的力度了

五、Actor-Critic

现在，我们终于开始学习顶顶大名的Actor-Critic了！

我们知道，MC的效率是相对比较低的，因为需要一直走到最终状态。所以我们希望用TD代替MC

什么是AC

关于AC，很多书籍和教程都说AC是DQN和PG的结合。个人觉得道理是怎么个道理，但其实是不够清晰，也很容易产生误读，甚至错误理解AC

PG利用带权重的梯度下降方法更新策略，而获得权重的方法是蒙地卡罗计算G值

蒙地卡罗需要完成整个游戏过程，直到最终状态，才能通过回溯计算G值，这使得PG方法的效率被限制

那我们可不可以更快呢？相信大家已经想到了，那就是改为TD

但改为TD还有一个问题需要解决：在PG，我们需要计算G值；那么在TD中，我们应该怎样估算每一步的Q值呢？

有没有发现，其实这个问题我们在学DQN的时候也遇到过， 熟悉的套路：我们用上万能的神经网络解决

也就是说，Actor-Critic，其实是用了两个网络：

两个网络有一个共同点，输入状态S: 一个输出策略，负责选择动作，我们把这个网络成为Actor； 一个负责计算每个动作的分数，我们把这个网络成为Critic

大家可以形象地想象为，Actor是舞台上的舞者，Critic是台下的评委

Actor在台上跳舞，一开始舞姿并不好看，Critic根据Actor的舞姿打分。Actor通过Critic给出的分数，去学习：如果Critic给的分数高，那么Actor会增加这个动作的输出概率；相反，如果Critic给的分数低，那么就减少这个动作输出的概率

AC是TD版本的PG

TD-error

在DQN预估的是Q值，在AC中的Critic，估算的是V值

你可能会说，为什么不是Q值呢？说好是给动作评价呢

我们可以直接用network估算的Q值作为更新值，但效果会不太好

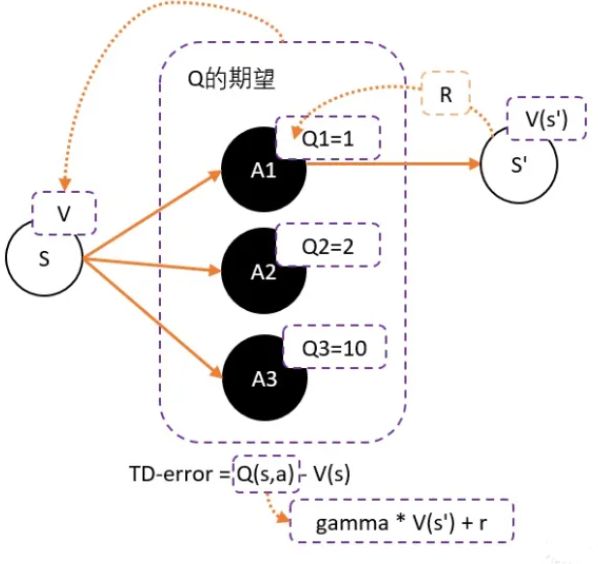
原因我们可以看下图：

假设我们用Critic网络，预估到S状态下三个动作A1，A2，A3的Q值分别为1,2,10

但在开始的时候，我们采用平均策略，于是随机到A1。于是我们用策略梯度的带权重方法更新策略，这里的权重就是Q值

于是策略会更倾向于选择A1，意味着更大概率选择A1，结果A1的概率就持续升高…

这就掉进了正数陷阱。我们明明希望A3能够获得更多的机会，最后却是A1获得最多的机会

这是为什么呢？

这是因为Q值用于是一个正数，如果权重是一个正数，那么我们相当于提高对应动作的选择的概率。权重越大，我们调整的幅度将会越大

其实当我们有足够的迭代次数，这个是不用担心这个问题的。因为总会有机会抽中到权重更大的动作，因为权重比较大，抽中一次就能提高很高的概率

但在强化学习中，往往没有足够的时间让我们去和环境互动。这就会出现由于运气不好，使得一个很好的动作没有被采样到的情况发生

要解决这个问题，我们可以通过减去一个baseline，令到权重有正有负。而通常这个baseline，我们选取的是权重的平均值。减去平均值之后，值就变成有正有负了

而Q值的期望(均值)就是V

所以我们可以得到更新的权重：Q(s,a)-V(s)

随之而来的问题是，这就需要两个网络来估计Q和V了。但马尔科夫告诉我们，很多时候，V和Q是可以互相换算的

Q(s,a)用gamma * V(s’) + r 来代替，于是整理后就可以得到：

gamma * V(s’) + r - V(s) —— 我们把这个差，叫做TD-error

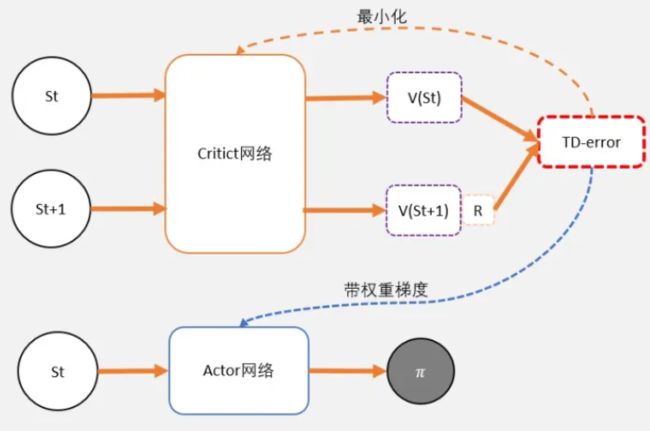
眼尖的同学可能已经发现，如果Critic是用来预估V值，而不是原来讨论的Q值。那么，这个TD-error是用来更新Critic的loss了

没错，Critic的任务就是让TD-error尽量小，然后TD-error给Actor做更新

现在我们再总结一下TD-error的知识：

1. 为了避免正数陷阱，我们希望Actor的更新权重有正有负。因此，我们把Q值减去他们的均值V，Q(s,a)-V(s)
2. 为了避免需要预估V值和Q值，我们希望把Q和V统一；由于Q(s,a) = gamma * V(s’) + r - V(s)，所以我们得到TD-error公式： TD-error = gamma * V(s’) + r - V(s)
3. TD-error就是Actor更新策略时候，带权重更新中的权重值
4. 现在Critic不再需要预估Q，而是预估V。而根据马可洛夫链所学，我们知道TD-error就是Critic网络需要的loss，也就是说，Critic函数需要最小化TD-error

大家看，其实AC没有很难，关键是对TD-error的理解。理解了TD-error，就能串起Actor和Critic两者

参考

1、怎样直观理解Qlearning算法：https://zhuanlan.zhihu.com/p/110338833

2、三维可视化助你直观理解DQN算法[DQN理论篇]：https://zhuanlan.zhihu.com/p/110620815

3、如何理解策略梯度（Policy Gradient）算法：https://zhuanlan.zhihu.com/p/110881517

4、理解Actor-Critic的关键是什么：https://zhuanlan.zhihu.com/p/110998399