【深度学习】多分类问题和多标签分类问题
上一章——激活函数
文章目录
- 什么是多分类问题
- Softmax
-
- 贝叶斯公式
- softmax的损失函数
- 多标签分类问题
什么是多分类问题
 在之前的课程中,我们学习了二分问题,二分问题中的所有数据会被分类为0和1(或者Ture和False)两种输出标签。但是在大多数情况下,分类问题的输出远远不止两种情况,例如之前在课程中举例的肿瘤问题,肿瘤被分为良性和恶性两种,但实际上会有更多的分类情况,它有可能是A型,B型,C型…我们将这种拥有2种以上输出标签的问题称为多分类问题。虽然输出y依旧只能取值有限的离散值,但是输出标签的种类将会有两个以上。
在之前的课程中,我们学习了二分问题,二分问题中的所有数据会被分类为0和1(或者Ture和False)两种输出标签。但是在大多数情况下,分类问题的输出远远不止两种情况,例如之前在课程中举例的肿瘤问题,肿瘤被分为良性和恶性两种,但实际上会有更多的分类情况,它有可能是A型,B型,C型…我们将这种拥有2种以上输出标签的问题称为多分类问题。虽然输出y依旧只能取值有限的离散值,但是输出标签的种类将会有两个以上。
MNIST被称为机器学习的“Hello World”,MNIST要求算法识别出不同的字迹所对应的数字,所有的阿拉伯数字总共有10个(0~9),MNIST就是一个典型的多分类问题。
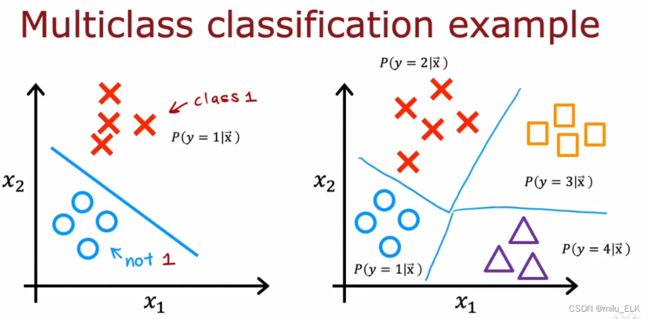
在二分问题中,我们的拟合方法是找到假设函数 g ( z ) g(z) g(z)中的决策边界z,那么推广到多分类问题中,也是同样的方法,二分问题只需一条决策边界,而往后的n分问题则需要n条决策边界。类比二分问题中我们使用的是逻辑回归,在多分问题中我们将学习Softmax算法。
Softmax
Softmax算法是对逻辑回归的推广和泛化,是一种针对多分类环境下的二元分类算法

首先我们要指出一点:所有离散值的预测概率之和一定为1。
以二分问题中的逻辑回归为例,假设 P ( y = 1 ∣ x ) = 0.71 P(y=1|x)=0.71 P(y=1∣x)=0.71,那么 P ( y = 0 ∣ x ) = 1 − 0.71 = 0.29 P(y=0|x)=1-0.71=0.29 P(y=0∣x)=1−0.71=0.29,
这个很好理解,因为输出结果不是0就是1,那么 P ( y = 1 ∣ x ) + P ( y = 0 ∣ x ) = 1 P(y=1|x)+P(y=0|x)=1 P(y=1∣x)+P(y=0∣x)=1,那么我们推广到多元


我们会发现Softmax的计算公式与Sigmoid相似,
Softmax: z j = w ⃗ j ⋅ x ⃗ + b j ( j = 1... N ) z_j=\vec w_j \cdot \vec x+b_j(j=1...N) zj=wj⋅x+bj(j=1...N)
a j = e z j ∑ k = 1 N e z k = P ( y = j ∣ x ⃗ ) a_j=\frac{e^{z_j}}{\sum^N_{k=1} e^{z_k}}=P(y=j|\vec x) aj=∑k=1Nezkezj=P(y=j∣x)
如果想要从数学上理解Softmax函数,我们必须先了解一个概念:
- 贝叶斯公式
贝叶斯公式
条件概率公式:
P ( x ∣ y ) = P ( x y ) P ( y ) P(x|y)=\frac {P(xy)}{P(y)} P(x∣y)=P(y)P(xy)
其中 P ( x ∣ y ) P(x|y) P(x∣y)代表在y事件已经发生的情况下x事件发生的概率, P ( x y ) P(xy) P(xy)代表事件xy都发生的概率,P(y)代表y事件发生的概率(无论x事件是否发生)
全概率公式:
P ( x ) = ∑ i = 1 n P ( y i ) P ( x ∣ y i ) P(x)=\displaystyle\sum^n_{i=1}P(y_i)P(x|y_i) P(x)=i=1∑nP(yi)P(x∣yi)
因此x事件发生的全概率是在每一种 y i y_i yi事件发生的情况下事件x发生的概率之和
贝叶斯公式:
P ( y i ∣ x ) = P ( x ∣ y i ) P ( y i ) P ( x ) = P ( x ∣ y i ) P ( y i ) ∑ j = 1 n P ( y i ) P ( x ∣ y j ) P(y_i|x)=\frac {P(x|y_i)P(y_i)}{P(x)}=\frac {P(x|y_i)P(y_i)}{\sum^n_{j=1}P(y_i)P(x|y_j)} P(yi∣x)=P(x)P(x∣yi)P(yi)=∑j=1nP(yi)P(x∣yj)P(x∣yi)P(yi)
其中根据条件概率公式我们知道 P ( x ∣ y i ) P ( y i ) = P ( x y i ) , P(x|y_i)P(y_i)=P(xy_i), P(x∣yi)P(yi)=P(xyi),即为x和 y i y_i yi事件都发生的概率,P(x)为x事件发生的全概率
因此 P ( y i ∣ x ) = P ( x y i ) P ( x ) P(y_i|x)=\frac {P(xy_i)}{P(x)} P(yi∣x)=P(x)P(xyi)
在二分类问题中,由于分类只有两种,因此事件y只有两项,如果我们将贝叶斯公式上下同时除以 P ( y 1 ) P ( x ∣ y 1 ) P(y_1)P(x|y_1) P(y1)P(x∣y1):
P ( y 1 ∣ x ) = P ( y 1 ) P ( x ∣ y 1 ) P ( y 1 ) P ( x ∣ y 1 ) + P ( y 2 ) P ( x ∣ y 2 ) P(y_1|x)=\frac {P(y_1)P(x|y_1)}{P(y_1)P(x|y_1)+P(y_2)P(x|y_2)} P(y1∣x)=P(y1)P(x∣y1)+P(y2)P(x∣y2)P(y1)P(x∣y1)
= 1 1 + P ( y 2 ) P ( x ∣ y 2 ) P ( y 1 ) P ( x ∣ y 1 ) =\frac {1}{1+\frac {P(y_2)P(x|y_2)}{P(y_1)P(x|y_1)}} =1+P(y1)P(x∣y1)P(y2)P(x∣y2)1
我们将 P ( y 2 ) P ( x ∣ y 2 ) P ( y 1 ) P ( x ∣ y 1 ) \frac {P(y_2)P(x|y_2)}{P(y_1)P(x|y_1)} P(y1)P(x∣y1)P(y2)P(x∣y2)设为 e − z e^{-z} e−z
P ( y 1 ∣ x ) = 1 1 + e − z P(y_1|x)=\frac {1}{1+e^{-z}} P(y1∣x)=1+e−z1
是不是有点眼熟?没错,这就是Sigmoid函数,
其中 z = l n P ( y 2 ) P ( x ∣ y 2 ) P ( y 1 ) P ( x ∣ y 1 ) z=ln\frac {P(y_2)P(x|y_2)}{P(y_1)P(x|y_1)} z=lnP(y1)P(x∣y1)P(y2)P(x∣y2),z与向量的关系请参考sigmoid与条件概率的关系及推导过程
之所以要设成e的指数形式,是为了防止概率出现负数,以e的指数形式表示是不会出现负数的
我们说softmax是Sigmoid的推广,你可以简单地把 P ( y 1 ∣ x ) 看作 t 1 t 1 + t 2 , P(y_1|x)看作\frac {t_1}{t_1+t_2}, P(y1∣x)看作t1+t2t1,则 P ( y 2 ∣ x ) = 1 − t 1 t 1 + t 2 = t 2 t 1 + t 2 P(y_2|x)=1-\frac {t_1}{t_1+t_2}=\frac {t_2}{t_1+t_2} P(y2∣x)=1−t1+t2t1=t1+t2t2,然后推广到n阶就有 P ( y N ∣ x ) = t N t 1 + . . . + t N P(y_N|x)=\frac {t_N}{t_1+...+t_N} P(yN∣x)=t1+...+tNtN,当然我只是从结果上讲,没有什么数学推理,具体原理贴在下面链接
本文只是简单地提一下概率论的一些基本知识,至于softmax公式的推导,如果还想深究里面的数学原理,可以看看这个视频,作者本人打算学完这个系列之后在复习这些内容:softmax是为了解决归一问题凑出来的吗?和最大熵是什么关系?最大熵对机器学习为什么非常重要?
softmax的损失函数
回到我们上面的内容,Softmax:
z j = w ⃗ j ⋅ x ⃗ + b j ( j = 1... N ) z_j=\vec w_j \cdot \vec x+b_j(j=1...N) zj=wj⋅x+bj(j=1...N)
a j = e z j ∑ k = 1 N e z k = P ( y = j ∣ x ⃗ ) a_j=\frac{e^{z_j}}{\sum^N_{k=1} e^{z_k}}=P(y=j|\vec x) aj=∑k=1Nezkezj=P(y=j∣x)
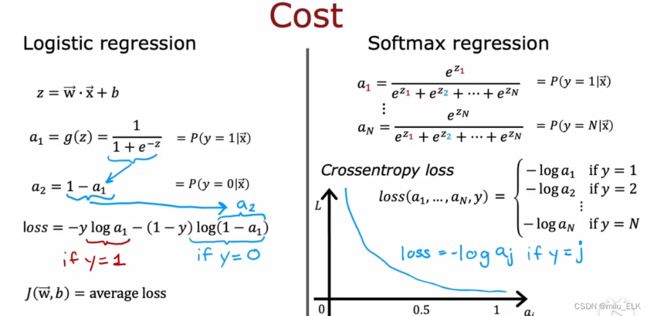
我们说Softmax是逻辑回归的推广,那么其损失函数也应当类似,
其中 l o s s ( a 1 , . . . . a N , y ) = { − l o g a 1 i f y = 1 − l o g a 2 i f y = 2 . . . − l o g a N i f y = N loss(a_1,....a_N,y)= \begin{cases} -log\space a_1 \space\space if \space y=1 \\ -log\space a_2 \space\space if \space y=2 \\ ... \\ -log\space a_N \space\space if \space y=N \end{cases} loss(a1,....aN,y)=⎩ ⎨ ⎧−log a1 if y=1−log a2 if y=2...−log aN if y=N
当概率 a i a_i ai越接近0,损失越大,其中N代表单层内神经元的个数
多标签分类问题
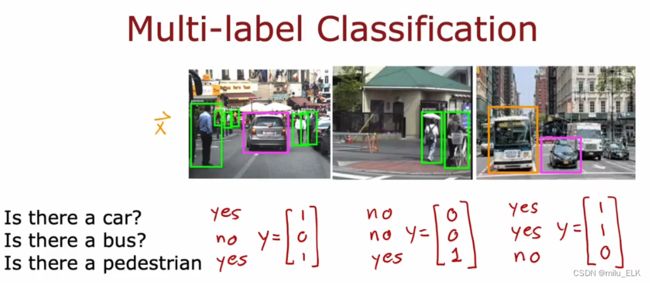
如果我们想要用人工智能来实现视觉识别,就像你平时在上网时遇到的一些验证题目:“为了验证您不是机器人,请找出图中的汽车”。我们想要实现对一张图片同时多处进行识别,以上图为例,识别图中是否有轿车?是否有公交车?是否有行人?
那么该例子中输入图片x,我们将会得到一个含三个数字的输出向量y。
注意:多标签分类问题和我们在上面所说的多分类问题并不是同一个东西,在多分类问题中,尽管有多种不同的取值,但我们最后得到的输出结果往往是数字y。其本质回答的是一个问题:预测值属于哪一类?
而在多标签分类问题中,最终的输出结果是一个含多个数字的向量,这意味着你可以认为它同时解答了多个问题:是否存在a?是否存在b?…是否存在n?在多分类问题中,最终结果只能是多个标签中的一个,但在多标签分类问题中最终结果可能是多个标签同时存在。
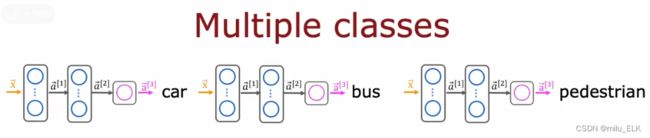
我们怎样去实现多标签分类问题?如果说回答三个问题,我们当然可以设计三个神经网络,来分别解决。但是这样未免也太浪费了,实际上由于这三个问题的结构都是一模一样的,本质上来说都是同样的算法,它们的隐藏层都是一样的,因此我们可以将它们进行合并。
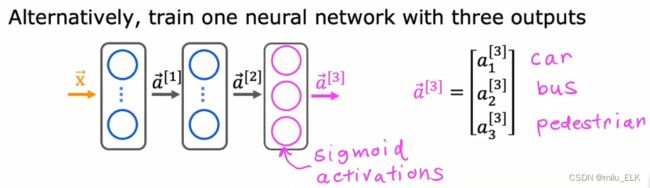
最终,我们可以构造这样的一个神经网络,唯一的区别在于输出层使用了多个神经元而非单个,相当于我们将上面的三个神经网络的输出层的神经元合并到同一个输出层。而且注意:在此处我们使用的是Sigmoid函数而非Softmax。不是说Softmax用于解决多个标签的分类问题吗?因为本质上该例子中需要预测的问题是三个二分问题,所以我们使用的是三个Sigmoid函数而非Softmax。
在学习中,不要搞混了多分类问题和多标签分类问题的概念。你可以简单理解为:多分类问题中的所有输出标签都是互斥的,如果是A那就不能是B、C…
而在多标签分类问题中,所有的输出标签并无互斥关系,输出有A也不影响输出B,它们可以同时存在。
下一章——模型评估