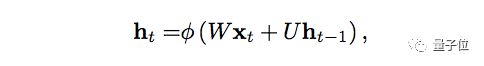干货 | 循环神经网络(RNN)和LSTM初学者指南
![]()
本文经AI新媒体量子位(公众号ID:qbitai )授权转载,转载请联系出处。
本文约5000字,建议阅读10分钟。
本文详细介绍了循环神经网络(RNN),及其变体长短期记忆(LSTM)背后的原理。
最近,有一篇入门文章引发了不少关注。文章中详细介绍了循环神经网络(RNN),及其变体长短期记忆(LSTM)背后的原理。
具体内容,从前馈网络(Feedforward Networks)开始讲起,先后讲述了循环神经网络、时序反向传播算法(BPTT)、LSTM等模型的原理与运作方式。
在文章的最后,也给出了有关LSTM的代码示例,以及LSTM超参数优化的注意事项和相关的阅读资料。
这篇文章来自Skymind,一家推动数据项目从原型到落地的公司。获得了YCombinator、腾讯等的投资。
对于人工智能初学者来说,是一份非常不错的入门资料。
循环网络,是一种人工神经网络(ANN),用来识别数据序列中的模式。
比如文本、基因组、笔记、口语或来自传感器、股票市场和政府机构的时间序列数据。
它的算法考虑了时间和顺序,具有时间维度。
研究表明,RNN是最强大和最有用的神经网络之一,它甚至能够适用于图像处理。
把图像分割成一系列的补丁,可以视为一个序列。
但是,想要理解循环网络,首先要必须了解前馈网络的基本知识。
前馈网络回顾
前馈网络和循环网络的命名,来自于它们在传递信息时,在网络节点上执行的一系列数学运算的方式。
前馈网络直接向前递送信息(不会再次接触已经经过的节点),而循环网络则是通过循环传递信息。
前馈网络中的样例,输入网络后被转换成输出;在监督学习中,输出将是一个标签,一个应用于输入的名称。
也就是说,前馈网络将原始数据映射到类别,识别出信号的模式。例如,输入图像应该被标记为“猫”还是“大象”。
前馈网络根据标记的图像进行训练,直到猜测图像类别时产生的错误最小化。 通过一组经过训练的参数(或者称为权重,统称为模型) ,网络就可以对它从未见过的数据进行分类了。
一个训练好的前馈网络可以应用在任何随机的照片数据集中,它识别的第一张照片,并不会影响它对第二张照片的预测。
看到一只猫的照片之后,不会导致网络预下一张图是大象。
也就是说,前馈网络没有时间顺序的概念,它考虑的唯一输入就是它所接触到的当前的输入样例。
循环网络
与前馈网络相比,循环网络的输入不仅包括当前的输入样例,还包括之前的输入信息。
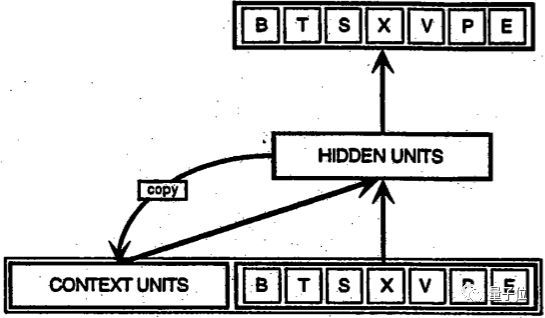
下面是美国加州大学圣地亚哥分校教授Jeffrey Elman提出的一个早期的简单循环网络的示意图。
图底部的BTSXPE代表当前时刻的输入样例,而CONTEXT UNIT代表前一时刻的输出。
循环网络在t-1个时间步的判定,会影响随后在t时间步的判定。所以,循环网络有两个输入源,现在和最近的过去,它们结合起来决定对新数据的反应,就像我们在生活中一样。
循环网络与前馈网络的区别在于,循环网络的反馈循环会连接到它们过去的判定,将自己的输出作为输入。
循环网络是有记忆的。给神经网络增加记忆的目的在于:序列本身带有信息,循环网络用它来执行前馈网络不能执行的任务。
这些连续的信息被保存在循环网络的隐藏状态中,这种隐藏状态管理跨越多个时间步,并一层一层地向前传递,影响网络对每一个新样例的处理。
循环网络,需要寻找被许多时刻分开的各种事件之间的相关性,这些相关性被称为“长距离依赖”,因为时间下游的事件依赖于之前的一个或多个事件,并且是这些事件的函数。
因此,你可以将RNN理解为是一种跨时间分享权重的方式。
正如人类的记忆在身体内无形地循环,影响我们的行为但不暴露全貌一样,信息也在循环网络的隐藏状态中循环。
用数学的方式来描述记忆传递的过程是这样的:
t代表时间步,ht代表第t个时间步的隐藏状态,是同一个时间步xt的输入函数。W是权重函数,用于修正xt。
U是隐藏状态矩阵,也被称为转移矩阵,类似于马尔可夫链。ht-1代表t的上一个时间步t-1的隐藏状态。
权重矩阵,是决定当前输入和过去隐藏状态的重要程度的过滤器。 它们产生的误差会通过反向传播返回,并用于调整相应的权重,直到误差不再降低。
权重输入(Wxt)和隐藏状态(Uht-1)的总和被函数φ压缩,可能是逻辑S形函数或者是双曲正切(tanh)函数,视情况而定。
这是一个标准工具,用于将非常大或非常小的值压缩到逻辑空间中,并使梯度可用于反向传播。
因为这个反馈循环发生在序列中的每个时间步中,每个隐藏状态不仅跟踪前一个隐藏状态,只要记忆能够持续存在,它会还包含h_t-1之前的所有的隐藏状态。
给定一系列字母,循环网络将使用第一个字符来帮助确定它对第二个字符的感知,比如,首字母是q,可能会导致它推断下一个字母是u,而首字母是t,可能会导致它推断下一个字母是h。
由于循环网络跨越时间,用动画来说明可能会更好。(可以将第一个垂直节点看作是一个前馈网络,随着时间的推移,它会变成循环网络)。
在上图中,每个x是一个输入样例,w是过滤输入的权重,a是隐藏层的激活(加权输入和先前隐藏状态的和),b是隐藏层使用修正线性或sigmoid单元转换或压缩后的输出。
时序反向传播算法(BPTT)
循环网络的目的是准确地对序列输入进行分类。主要依靠误差的反向传播和梯度下降法来做到这一点。
前馈网络中的反向传播从最后的误差开始,经过每个隐藏层的输出、权重和输入反向移动,将一定比例的误差分配给每个权重,方法是计算它们的偏导数∂e/∂w,或它们之间的变化率之间的关系。
随后,这些偏导数会被用到梯度下降算法中,来调整权重减少误差。
而循环网络依赖于反向传播的一种扩展,称为时序反向传播算法,即BPTT。
在这种情况下,时间通过一系列定义明确、有序的计算来表达,这些计算将一个时间步与下一个时间步联系起来。
神经网络,无论是循环的还是非循环的,都是简单的嵌套复合函数,比如f(g(h(x))。添加时间元素,只是扩展了我们用链式法则计算导数的函数序列。
截断式BPTT
截断式BPTT(Truncated BPTT)是完整BPTT的近似方法,是处理是长序列的首选。
在时间步较多的序列中,完整BPTT的每个参数更新的正向/反向运算成本变得非常高。
截断式BPTT的缺点是,由于截断,梯度反向移动的距离有限,因此网络无法学习与完整BPTT一样长的依赖。
梯度消失和梯度爆炸
和大多数神经网络一样,循环网络也有了一定的历史。 到1990年代初,梯度消失问题成为影响网络性能的主要障碍。
就像直线表示x的变化和y的变化一样,梯度表示所有权重随误差变化的变化。如果我们不知道梯度,我们就不能在减少误差的方向上调整权重,网络也就会停止学习。
循环网络,在最终的输入和之前许多时间步之间建立联系时,也遇到了问题。因为很难知道一个远距离的输入有多么重要。
就像向前追溯曾曾曾曾曾……祖父母兄弟的数量一样,会越来越多,越来越多。
这在一定程度上是因为,通过神经网络传递的信息要经过多个乘法阶段。
每个研究过复利的人都知道,任何数量循环乘以略大于一的量,都会变得不可估量的大(实际上,简单的数学真理支撑着网络效应和社会不平等)。
反过来,乘以小于1的量,也会变得非常非常小。如果赌徒们每投入一美元,只能赢得97美分,那么他们很快就会破产。
由于深度神经网络的层和时间步通过乘法相互关联,导数很容易消失或爆炸。
梯度爆炸时,每一个权重就像谚语中的蝴蝶一样,它拍打的翅膀会引起远处的飓风。
但是梯度爆炸解决起来相对容易,因为它们可以被截断或压缩。
梯度消失正好相反,是导数变得非常小,使计算机无法工作,网络也无法学习。这是一个更难解决的问题。
下面你可以看到一遍又一遍应用S形函数的效果。 数据曲线越来越平缓,直至在较长的距离上无法检测到斜率。 这类似于通过许多层的梯度消失。
长短期记忆(LSTM)
在90年代中期,德国研究人员Sepp Hochreiter和Juergen Schmidhuber提出了一种具有长短期记忆单元( LSTM )的循环网络变体,作为梯度消失问题的解决方案。
LSTM有助于保留可以通过时间和层进行反向传播的误差。
通过保留一个更为恒定的误差,它们使循环网络能够在有许多时间步(超过1000步)的情况下继续学习,从而打开一个远程链接因果关系的通道。
这是机器学习和人工智能面临的主要挑战之一,因为算法经常遇到奖励信号稀疏和延迟的环境。
LSTM将信息存放在循环网络正常信息流之外的门控单元中。信息可以像计算机内存中的数据一样存储、写入单元,或者从单元中读取。
单元通过打开和关闭的门来决定存储什么,以及何时允许读取、写入和忘记。
但与计算机上的数字存储器不同,这些门是模拟的,通过范围在0~1之间的sigmoid函数的逐元素相乘来实现。
与数字信号相比,模拟信号的优势是可微分,因此适用于反向传播。
这些门类似于神经网络的节点,会根据它们接收到的信号决定开关,它们根据信息的强度和重要性来阻止或传递信息,然后用它们自己的权重过滤这些信息。
这些权重,就像调整输入和隐藏状态的权重一样,可以在循环网络学习过程中进行调整。
也就是说,记忆单元学习会通过猜测、反向传播误差和梯度下降法调整权重的迭代过程,来决定何时允许数据进入、离开或删除。
下图说明了数据如何通过记忆单元,以及门如何控制数据流动。
如果你刚刚接触LSTM,不要着急,仔细研究一下。只需要几分钟,就能揭开其中的秘密。
从底部开始,三个箭头显示,信息由多个点流入记忆单元。 当前输入和过去单元状态的组合不仅反馈到单元本身,而且反馈到它的三个门中的每一个,这将决定它们如何处理输入。
黑点是门本身,决定是否让新的输入进入、遗忘当前的状态,还是让这一状态在当前时间步影响网络的输出。
Sc是记忆单元的当前状态,g_y_in是记忆单元的当前输入。
请记住,每个门都可以打开或关闭,它们会在每一步重新组合它们的打开和关闭状态。记忆单元,在每个时间步都可以决定,是否遗忘、写入、读取它的状态,这些流都表示出来了。
大的、加粗的字母,给出了每个操作的结果。
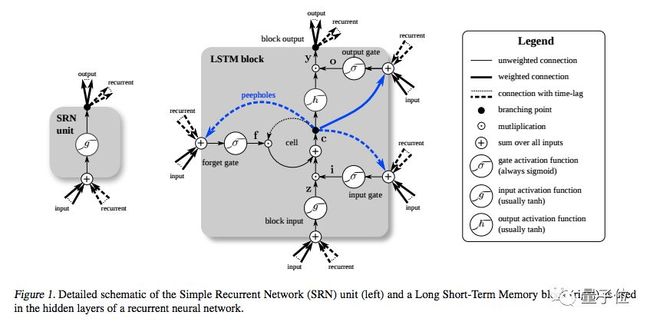
下面是另一个示意图,对比了简单的循环网络(左)和 LSTM 单元(右)。
值得注意的是,LSTM的记忆单元在输入转换中赋予加法和乘法不同的角色。
两个图中的中心加号,本质上就是 LSTM 的秘密。
虽然这看起来非常非常简单,但当必须在深度上反向传播时,这种变化有助于保持恒定的误差。
LSTM不是将当前状态乘以新的输入来确定后续的单元状态,而是将两者相加,这就产生了差异。(用于遗忘的门仍然依赖于乘法。)
不同的权重集对输入信息进行筛选,决定是否输入、输出或遗忘。
不同的权重集对输入信息进行过滤,决定是否输出或遗忘。遗忘门被表示为一个线性恒等式函数,因为如果门是打开的,那么记忆单元的当前状态就会被简单地乘以1,从而向前传播一个时间步。
此外,有一个简单的窍门。将每个LSTM记忆单元遗忘门的偏差设定为1,可以提升网络性能。(但另一方面,Sutskever建议将偏差设定为5。)
你可能会问,LSTM的目的是将远距离事件与最终的输出联系起来,为什么它们会有一个遗忘门?
好吧,有时候遗忘是件好事。
如果分析一个文本语料库,在到达一个文档的末尾时,下一个文档基本上跟它没有关系,因此,在网络摄取下一个文档的第一个元素之前,应该将记忆单元设置为零。
以分析一个文本语料库为例,在到达文档的末尾时,你可能会认为下一个文档与这个文档肯定没有任何联系,所以记忆单元在开始吸收下一个文档的第一项元素前应当先归零。
在下图中,你可以看到在工作的门,直线表示关闭的门,空白圆圈代表打开的门。沿着隐藏层水平延伸的线条和圆圈是表示遗忘门。
需要注意的是,前馈网络只是一对一,即将一个输入映射到一个输出。但循环网络可以一对多,多对多,多对一。
涵盖不同时间尺度和远距离依赖
你可能还想知道,保护记忆单元不受新数据进入的输入门和防止它影响 RNN 的某些输出的输出门的精确值是多少。你可以把 LSTM 看作是,允许一个神经网络同时在不同的时间尺度上运行。
让我们以一个人的生命为例,想象一下我们在一个时间序列中收到了关于那个生命的各种数据流。
每个时间步的地理位置,对于下一个时间步来说都非常重要,因此时间尺度总是对最新信息开放的。
也许这个人是一个勤奋的公民,每两年投票一次。在民主时代,我们会特别关注他们在选举前后的所作所为。我们不想让地理位置持续产生噪音影响我们的政治分析。
如果这个人也是一个勤奋的女儿,那么也许我们可以构建一个家庭时间,学习每周日定期打电话的模式,每年假期前后,打电话的数量都会激增。这与政治周期或地理位置无关。
其他的数据也是这样。音乐是多节奏的。文本中包含不同时间间隔的重复主题。股票市场和经济会有更长的波动周期。它们在不同的时间尺度上同时运行,LSTM可以捕捉到这些时间尺度。
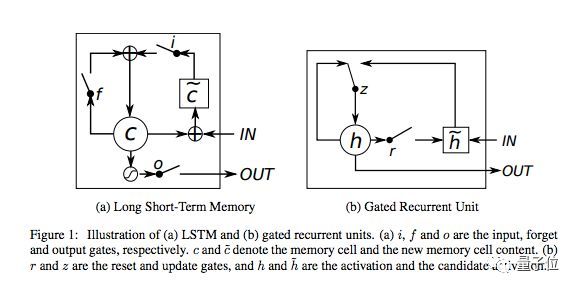
门控循环单元(GRU)
门控循环单元( GRU )基本上是没有输出门的LSTM,因此在每个时间步,它都将内容从其记忆单元完全写入到较大的网络中。
代码示例
这里示例,是一个LSTM如何学习复制莎士比亚戏剧的评论,使用Deeplearning4j实现。在难以理解的地方,都有相应的注释。
传送门:
https://github.com/deeplearning4j/dl4j-examples/blob/master/dl4j-examples/src/main/java/org/deeplearning4j/examples/recurrent/character/LSTMCharModellingExample.java
LSTM超参数调整
以下是手动优化RNN超参数时需要注意的一些情况:
小心过拟合,神经网络基本在“记忆”训练数据时,就会发生过拟合。过拟合意味着你在训练数据上有很好的表现,在其他数据集上基本无用。
正则化有好处:方法包括 l1、 l2和dropout等。
要有一个单独的测试集,不要在这个测试集上训练网络。
网络越大,功能就越强,但也更容易过拟合。 不要试图从10000个示例中学习一百万个参数,参数>样例=麻烦。
数据越多越好,因为它有助于防止过度拟合。
训练要经过多个epoch(算法遍历训练数据集)。
每个epoch之后,评估测试集表现,以了解何时停止(要提前停止)。
学习速率是最重要的超参数。
总体而言,堆叠层会有帮助。
对于LSTM,可以使用softsign(而不是softmax)函数替代双曲正切函数,它更快,更不容易饱和( 梯度大概为0 )。
更新器:RMSProp、AdaGrad或Nesterovs通常是不错的选择。AdaGrad也会降低学习率,这有时会有所帮助。
记住,要将数据标准化、MSE损失函数+恒等激活函数用于回归、Xavier权重初始化。
资源推荐
DRAW: A Recurrent Neural Network For Image Generation(论文)
https://arxiv.org/pdf/1502.04623v2.pdf
Gated Feedback Recurrent Neural Networks(论文)
https://arxiv.org/pdf/1502.02367v4.pdf
Recurrent Neural Networks;Juergen Schmidhuber(博客)
http://people.idsia.ch/~juergen/rnn.html
The Unreasonable Effectiveness of Recurrent Neural Networks; Andrej Karpathy(博客)
https://karpathy.github.io/2015/05/21/rnn-effectiveness/
Understanding LSTMs; Christopher Olah(博客)
https://colah.github.io/posts/2015-08-Understanding-LSTMs/
Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling; Cho et al(论文)
https://arxiv.org/pdf/1412.3555v1.pdf
Training Recurrent Neural Networks; Ilya Sutskever’s Dissertation(博士论文)
https://www.cs.utoronto.ca/~ilya/pubs/ilya_sutskever_phd_thesis.pdf
Long Short-Term Memory in Recurrent Neural Networks; Felix Gers(博士论文)
http://www.felixgers.de/papers/phd.pdf
LSTM: A Search Space Oddyssey; Klaus Greff et al(论文)
https://arxiv.org/pdf/1503.04069.pdf
原文链接:
https://skymind.ai/wiki/lstm
![]()
![]()