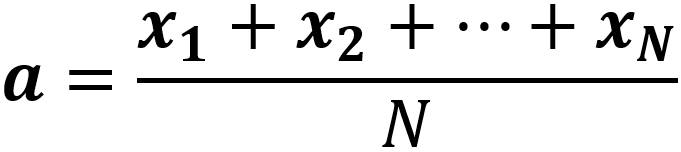Pytorch注意力机制下的向量相加
一、期望
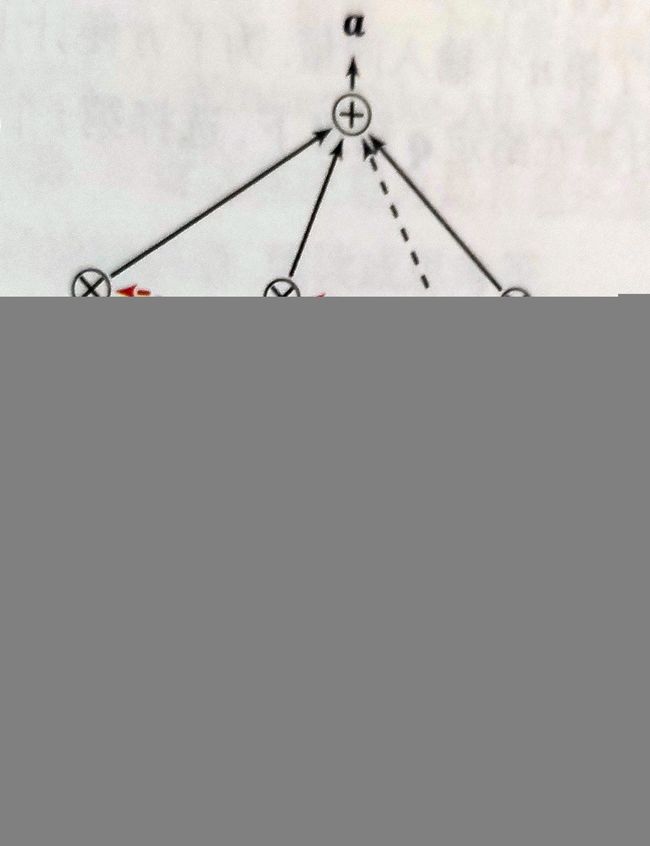
软性注意力机制(Soft Attention Mechanism)是一种常见的注意力机制。假设输入N个向量,输出为1个向量,那么软性注意力机制的核心思想是设计一个打分函数s,用于计算输入的每一个向量的分数,然后通过softmax计算公式求得每个向量的权重,最终运用向量线性相加的方式得到最终的1个向量。如下图所示:
实际上打分函数s还要输入一个查询向量q,但是这个q是根据具体任务来指定的,因此上图中我没有标注出q向量。
假设有N个向量,每个向量的注意力权重也有对应N个,注意力机制下的向量相加可描述为
假如没有注意力,那么注意力权重都相等,且为1/N,计算方式如下:
二、实现
注意力机制下
import torch
# 设置打印偏好
torch.set_printoptions(linewidth=1024, precision=2)
# 注意力权重
w = torch.tensor([[0.0, 0.0, 0.0, 1.0],
[0.0, 0.0, 0.5, 0.5]])
# 4个输入向量,batch size为2
x = torch.tensor([[[0.1, 0.1, 0.2], [0.8, 0.8, 0.8], [0.0, 0.0, 0.0], [0.8, 0.8, 1.0]],
[[0.2, 0.2, 0.6], [0.0, 0.0, 0.6], [0.5, 0.5, 0.5], [1.0, 1.0, 0.6]]])
# 4个向量根据权重线性相加
rw = w.reshape(w.shape[0], w.shape[1], 1)
a = (rw * x).sum(dim=1)
# 打印
print(w)
print(x)
print(a)
输出
tensor([[0.00, 0.00, 0.00, 1.00],
[0.00, 0.00, 0.50, 0.50]])
tensor([[[0.10, 0.10, 0.20],
[0.80, 0.80, 0.80],
[0.00, 0.00, 0.00],
[0.80, 0.80, 1.00]],[[0.20, 0.20, 0.60],
[0.00, 0.00, 0.60],
[0.50, 0.50, 0.50],
[1.00, 1.00, 0.60]]])
tensor([[0.80, 0.80, 1.00],
[0.75, 0.75, 0.55]])
无注意力的情况下
import torch
# 设置打印偏好
torch.set_printoptions(linewidth=1024, precision=2)
# 4输入向量,batch size为2
x = torch.tensor([[[0.1, 0.1, 0.2], [0.8, 0.8, 0.8], [0.0, 0.0, 0.0], [0.8, 0.8, 1.0]],
[[0.2, 0.2, 0.6], [0.0, 0.0, 0.6], [0.5, 0.5, 0.5], [1.0, 1.0, 0.6]]])
# 计算最终的输出向量
a = (x.sum(dim=1) / x.shape[1]).unsqueeze(1)
# 打印
print(x)
print(a)
输出
tensor([[[0.10, 0.10, 0.20],
[0.80, 0.80, 0.80],
[0.00, 0.00, 0.00],
[0.80, 0.80, 1.00]],[[0.20, 0.20, 0.60],
[0.00, 0.00, 0.60],
[0.50, 0.50, 0.50],
[1.00, 1.00, 0.60]]])
tensor([[[0.43, 0.43, 0.50]],[[0.43, 0.43, 0.58]]])
三、参考
神经网络与深度学习,邱锡鹏,机械工业出版社,199-203