数据结构【二叉搜索树模拟实现、LeetCode刷题】
目录
二叉搜索树性质
Insert非递归版本
递归版本：类private内部定义，因为需要显示传参root
Erase非递归版本
Erase递归版本
Find非递归版本
Find递归版本
构造/析构/拷贝构造/operator=
二叉搜索树性能
LeetCode刷题
根据二叉树创建字符串
二叉树的层序遍历
二叉树的最近公共祖先
二叉搜索树与双向链表_牛客题霸_牛客网
从前序与中序遍历序列构造二叉树
从中序与后序遍历序列构造二叉树
二叉树前序非递归遍历
二叉树中序非递归遍历
二叉树后序非递归遍历
二叉搜索树性质
1.若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
2.若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
3.它的左右子树也分别为二叉搜索树
注意事项：
1.搜索树不允许重复冗余数据
2.搜索二叉树中序遍历是有序+去重
3.二叉搜索树不支持修改
4.二叉搜索树也称二叉排序树
二叉搜索树结构
template
class BSTreeNode
{
BSTreeNode* _left;
BSTreeNode* _right;
K _key;
};
template
class BSTree
{
typedef BSTreeNode Node;
private:
Node* _root = nullptr;
}; 二叉搜索树的查找
从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
最多查找高度次，到空还没找到，这个值不存在
Insert非递归版本
返回值为bool，防止冗余数据
树为空，则直接新增节点，赋值给root指针
树不空，按二叉搜索树性质查找插入位置，插入新节点
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if(cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;//值在树中存在，错误
}
}
cur = new Node(key); //单纯写一句这个错误，cur只是局部变量，并没有挂到树中
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}递归版本：类private内部定义，因为需要显示传参root
此处递归插入需要加上&， 如果不加引用此处是局部变量，还需要链接父亲，如果加引用即可解决
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key == key)
return false;
else if (root->_key < key)
return _InsertR(root->_right, key);
else
return _InsertR(root->_left, key);
}Erase非递归版本
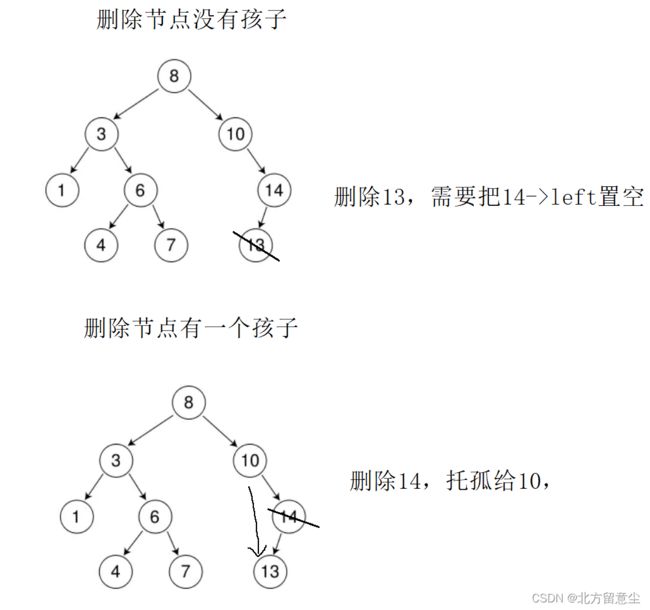图1，0/1个孩子的节点，把另一个孩子托孤给父亲，两个情况可以归类到一起
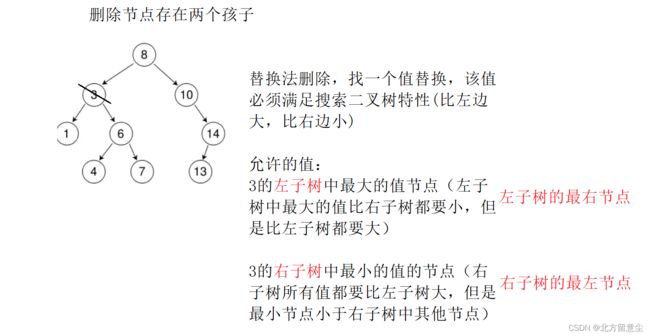图2，第三种情况
图3，第三种情况替换节点4赋值给删除节点3后，删除已替换节点3,替换节点要么没有孩子，要么只有一个孩子，可以直接删除
图4，归类图1的0/1个节点情况
图四还有一种例外，那就是删除root节点时，parent==null，解应用parent->崩溃，遇到只有1个节点的情况下删除根，更新根即可
图5，归纳图2，3的第三种情况
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else//已经找到要删除的节点，准备开始删除
{
if (cur->_left == nullptr)//如果要删除节点的左为null
{
if (cur == _root)//parent有可能为空，就是当要删除数据为root时
{
_root = cur->_right;//指向不为null的
}
else
{
if (cur == parent->_left)//cur有可能是父亲的左，也有可能是右，看图4
{
parent->_left = cur->_right;//默认托孤
}
else
{
parent->_right = cur->_right;//默认托孤
}
delete cur;
cur = nullptr;
}
}
else if(cur ->_right == nullptr)
{
if (cur == _root)//parent有可能为空，就是当要删除数据为root时
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else//左右都不为空,替换法删除，看图2，3，5
{
Node* min = cur->_right;//找到右子树最小节点替换
//Node* minParent = nullptr;
Node* minParent = cur; //看图5
while (min->_left)
{
minParent = min;
min = min->_left;
}
swap(cur->_key, min->_key);
if (min == minParent->_left)//看图5
minParent->_left = min->_right;
else
minParent->_right = min->_right;
delete min;
}
return true;
}
}
return false;
}Erase递归版本
当找到需要删除的位置时，分情况讨论：
1.如果需要删除的位置left为空，由于是递归和引用root->_right/left，直接把root->right不为空的值给root，让root->right替代root，记录root节点删除即可
2.当删除节点左右都不为空，root是删除位置，找到右子树最左节点后和root值交换，在root的右子树中查找删除交换的最左节点
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key == key)
{
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* min = root->_right;
while (min->_left)
{
min = min->_left;
}
swap(root->_key, min->_key);
return _EraseR(root->_right, key);
}
return true;
}
else if (root->_key < key)
return _EraseR(root->_right, key);
else
return _EraseR(root->_left, key);
}Find非递归版本
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return true;//值在树中存在
}
}
return false;
}Find递归版本
bool FindR(const K& key)
{
return _Find(_root,key);
}
private:
Node* _root = nullptr;
bool _Find(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key == key)
return true;
else if (root->_key < key)
return _Find(root->_right, key);
else
return _Find(root->_left, key);
}构造/析构/拷贝构造/operator=
注意事项：
1.构造函数后面加default，强制编译器生成默认构造函数
2.写了拷贝构造函数后必须得写构造函数，拷贝构造和构造都属于构造函数，写了一个另一个编译器就不会默认生成
3.operator=现代写法，当完成拷贝构造的深拷贝即可实现，在operator的参数阶段便生成临时对象，正好是赋值对象需要
~BSTree()
{
Destory(_root);
}
//BSTree()
//{
//
//}
BSTree() = default;//强制编译器生成默认构造函数
BSTree(const BSTree& k)
{
_root = _Copy(k._root);
}
BSTree& operator=(BSTree k)
{
swap(_root, k._root);
return *this;
}
private:
Node* _root = nullptr;
Node* _Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newnode = new Node(root->_key);
newnode->_left = _Copy(root->_left);
newnode->_right = _Copy(root->_right);
return newnode;
}
void Destory(Node* root)
{
if (root == nullptr)
return;
Destory(root->_left);
Destory(root->_right);
delete root;
} 二叉搜索树性能
插入和删除都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二 叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树
最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：O（log2 N）
最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为：O(N)，二叉搜索树失去性能。
如果要改进，不论按照什么次序插入关键码，二叉搜索树的性能都能达到最优的树：AVL树，红黑树
LeetCode刷题
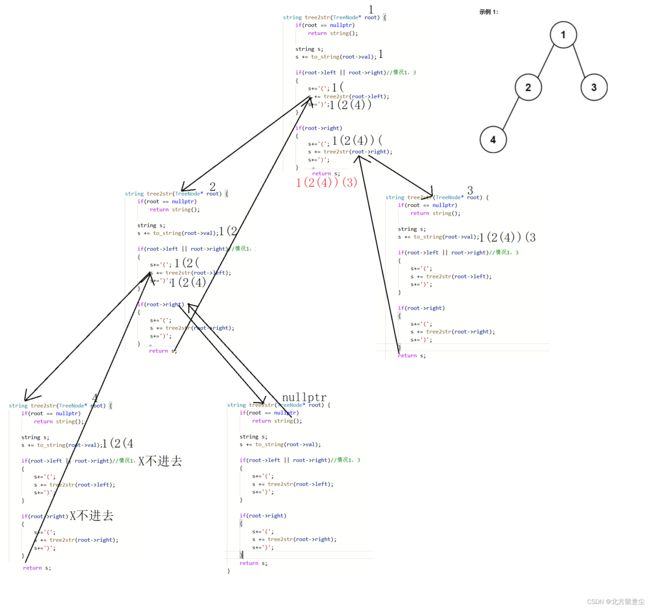
根据二叉树创建字符串
思路：
1.如果左右都为空，两个括号省略
2.右子树为空，左子树不为空，省略右子树括号
3.左子树为空，右子树不为空，不省略左子树括号，原因在于省略不确定子树是左/右
class Solution {
public:
string tree2str(TreeNode* root) {
if(root == nullptr)
return string();
string s;
s += to_string(root->val);
if(root->left || root->right)//情况1，3
{
s+='(';
s += tree2str(root->left);
s+=')';
}
if(root->right)
{
s+='(';
s += tree2str(root->right);
s+=')';
}
return s;
}
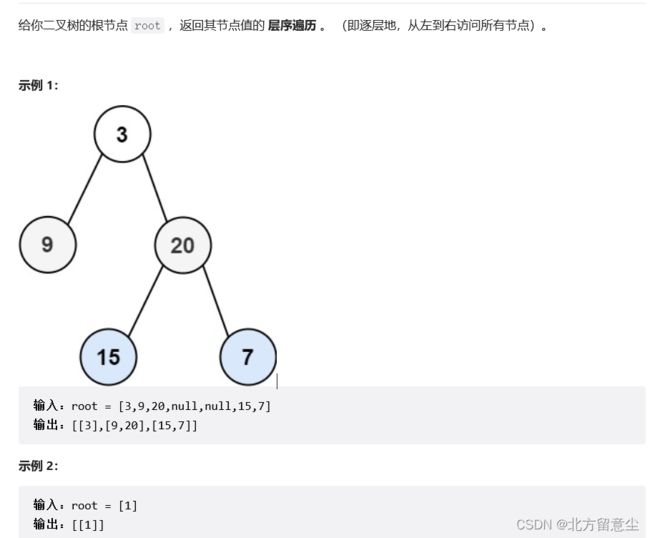
};二叉树的层序遍历
思路：
1.一层放一行，很难确定数据放在哪一行，我们定义一个levelsize，一层一层出，出完第一层后levelsize--，进第二层数据，第二层数据个数就是levelsize的长度
class Solution {
public:
vector> levelOrder(TreeNode* root) {
queue q;
int levelsize = 0;
if(root)
{
q.push(root);
levelsize = 1;
}
vector> vv;
while(!q.empty() && levelsize != 0)//控制队列
{
vector v;
for(size_t i = 0; i < levelsize;++i)//控制每一层的出
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
levelsize = q.size();
}
return vv;
}
}; 二叉树的最近公共祖先
规律：
1.节点中，一个是左子树中的节点，一个是右子树中的节点，则该节点就是最近祖先节点
2.都在当前节点的左子树中，则最近公共祖先一定在左子树中，右树同理
3.如果当前节点是一个指定节点，当前节点左右子树中有另一个节点，则当前节点是最近公共祖先
4.题目说明：p 和 q 均存在于给定的二叉树中。
class Solution {
public:
bool Find(TreeNode* sub ,TreeNode* x)
{
if(sub == nullptr)
return false;
if(sub == x)
return true;
return Find(sub->left,x) || Find(sub->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
if(root == p || root == q)//如果相等就是最近公共祖先，规律3
{
return root;
}
//此时p，q在子树中
bool pInLeft,pInRight,qInLeft,qInRight;
pInLeft = Find(root->left,p);
pInRight = !pInLeft;//p在左边就不再右边，否则上面的判断直接返回root
qInLeft = Find(root->left,q);
qInRight = !qInLeft;//q在左边就不再右边，否则上面的判断直接返回root
if((pInLeft && qInRight ) || (qInLeft && pInRight))//规律1
return root;
else if(qInLeft && pInLeft)//规律2
return lowestCommonAncestor(root->left,p,q);
else if(qInRight && pInRight)//规律2
return lowestCommonAncestor(root->right,p,q);
return nullptr;
}
};找路径写法
利用栈辅助完成，入节点后按前序思路入栈，如果一个节点走到nullptr并且和需要找的节点不相等，把该节点出栈（该节点所没有子树无法找到），继续寻找子树，找到对应节点层层返回true即可，此时栈中的节点就是路径
对比两个栈中的节点(栈倒着)，按照链表相交思路长的先pop掉，最后相等一起走即可找出
class Solution {
public:
bool findPair(TreeNode* root,TreeNode* x, stack& s)
{
if(root == nullptr)
return false;
s.push(root);
if(root == x)
return true;
if(findPair(root->left,x,s))
return true;
if(findPair(root->right,x,s))
return true;
s.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack ps;
stack qs;
findPair(root,p,ps);//不接收返回值是因为pq一定在里面
findPair(root,q,qs);
//类似链表相交
while(ps.size() != qs.size())
{
if(ps.size() > qs.size())
ps.pop();
else
qs.pop();
}
while(ps.top() != qs.top())
{
ps.pop();
qs.pop();
}
return ps.top();
}
}; 二叉搜索树与双向链表_牛客题霸_牛客网
要求：
不能创建任何新的结点，只能调整树中结点指针的指向。树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
思路：
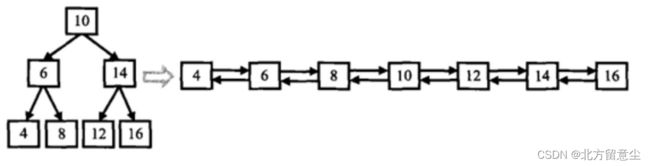
1.left指向中序的前一个位置，right指向中序的下一个位置，此时我们需要定义两个指针prev和cur，prev用来存储前一个位置，cur存储当前位置
2.按照中序的思路递归，当指向最左节点时此节点为cur，prev先为nullptr，让cur->left == nullptr,即可算出中序的前一个位置left，但是此时不知道cur->right是什么，先继续往下走让prev == cur
3.此时cur是6，prev是4，让cur->left = prev,但是不知道cur的right，但是此时我们知道prev的right,此时prev的right就是cur
4.继续重复2，3步的动作，一直持续到cur == 16，prev == 14，cur此时的right无法再递归，但是也可以结束，因为此时cur是最后一个节点，cur->right就是为nullptr
class Solution {
public:
void InOrderConvert(TreeNode* cur,TreeNode*& prev)
{
if(cur == nullptr)
return;
InOrderConvert(cur->left,prev);
cur->left = prev;
if(prev)
prev->right = cur;
prev = cur;
InOrderConvert(cur->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
TreeNode* prev = nullptr;
InOrderConvert(pRootOfTree, prev);
//要返回链表的头，但是此时链表的头是10
TreeNode* head = pRootOfTree;
while(head && head->left)
{
head = head->left;
}
return head;
}
};
从前序与中序遍历序列构造二叉树
注意：
1.前序和后序无法确定唯一一颗树，必须是前中/中后
知道前序和中序，如何构建二叉树？
大思路：前序构建树，中序分割左右子树
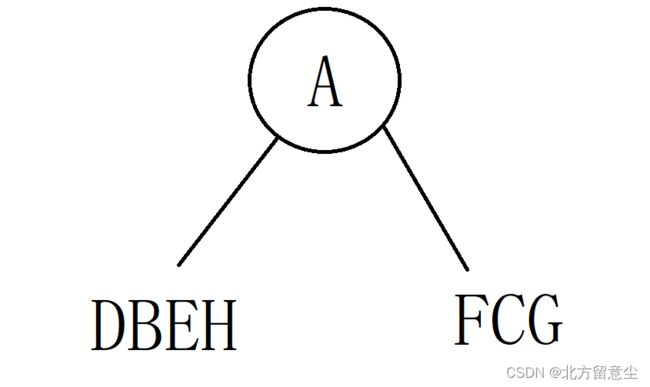
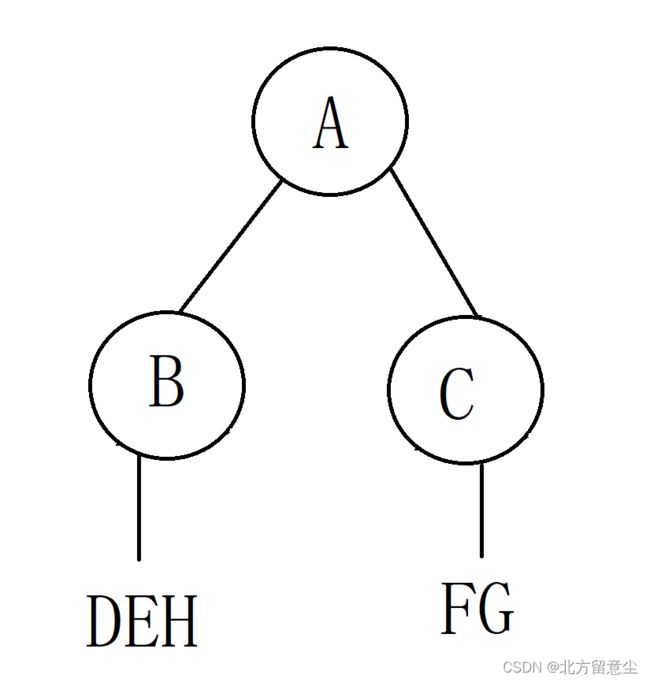
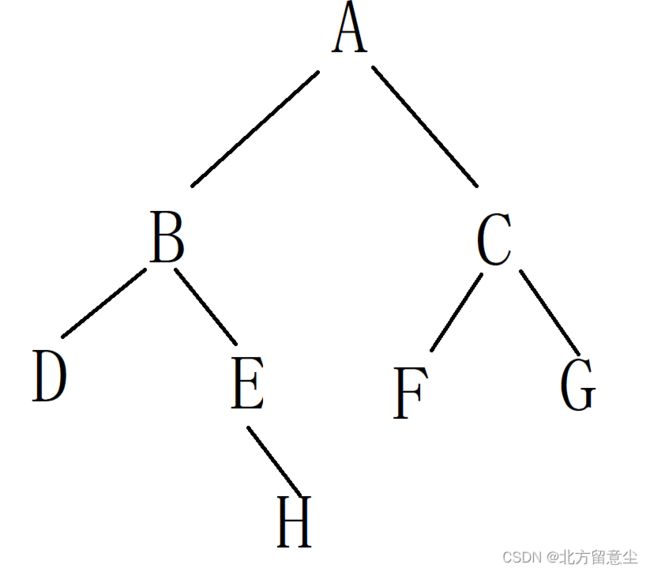
已知一颗二叉树前序为：ABDEHCFG，中序为DBEHAFCG，构建出二叉树
第一步：前序第一个字母为二叉树顶点，得顶点为A
第二步：在中序序列找到A的位置，排在A左边的所有字母（DBEH）组成左子树，排在A右边的所有字母（FCG）组成右子树。
第三步 ，看中序序列左子树部分（DBEH）在前序序列（BDEH）中的顺序，由于B排在前序序列第一个，B就是左子树的根结点。
看中序序列右子树部分（FCG）在前序序列（CFG）中的顺序，由于C排在前序序列第一个，C就是右子树的根结点。
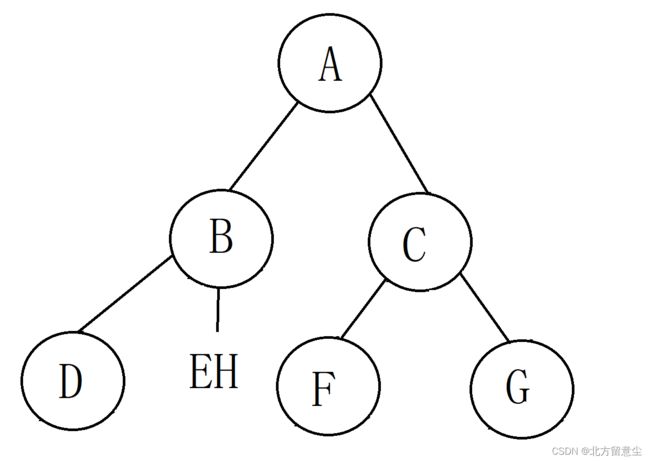
已知一颗二叉树前序为：ABDEHCFG，中序为DBEHAFCG，构建出二叉树
第四步，重复上述第二三步
中序序列中左子树部分（DEH），因为D在根结点B左边，所以D是B的左子树，中序序列中EH在B的右边，所以EH是B的右子树；
中序序列右子树部分（FG），因为F在根结点C左边，所以F组成C的左子树；因为G在根结点C的右边，所以G组成C的右子树。
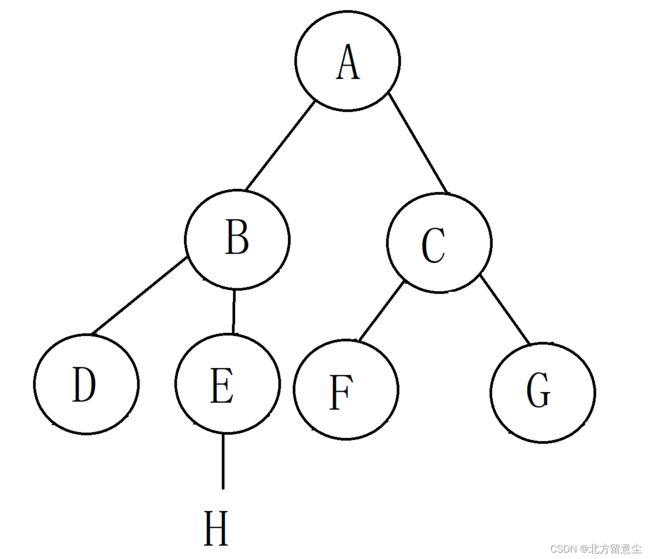
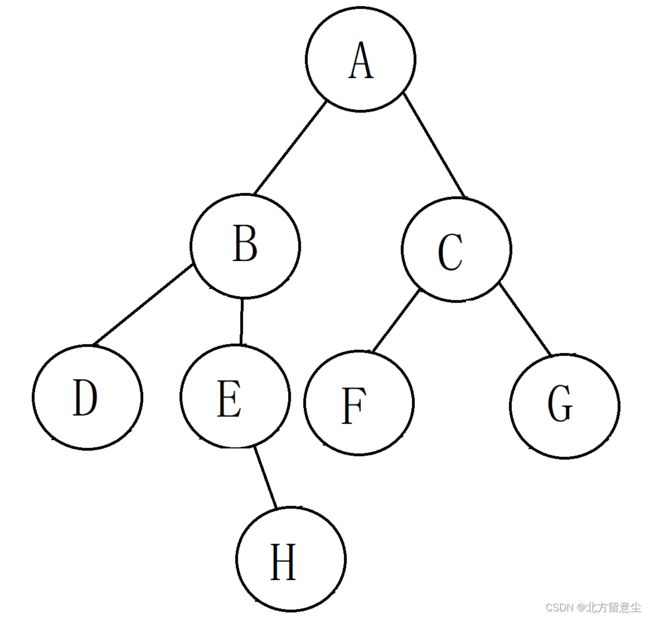
已知一颗二叉树前序为：ABDEHCFG，中序为DBEHAFCG，构建出二叉树
第五步，看前序序列（EH）可知E在第一个，所以E就是B的右子树的根结点
第六步，看中序序列H在E的右边，可以确定H是E的右子树
至此二叉树构建完成
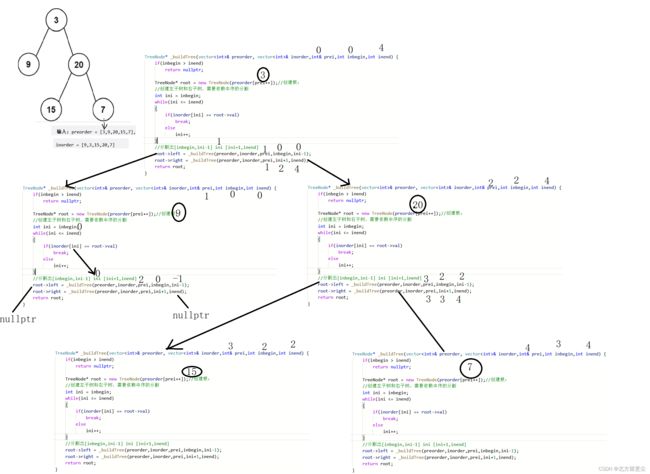
回到题目，我们让前序序列preorder用下标标识，中序序列使用区间标识。
创建根，分割左右递归创建左右子树，所有的节点创建都是前序，中序决定是否继续创建子树
class Solution {
public:
TreeNode* _buildTree(vector& preorder, vector& inorder,int& prei,int inbegin,int inend) {
if(inbegin > inend)
return nullptr;
TreeNode* root = new TreeNode(preorder[prei++]);//创建根；
//创建左子树和右子树，需要依赖中序的分割
int ini = inbegin;
while(ini <= inend)
{
if(inorder[ini] == root->val)
break;
else
ini++;
}
//分割出[inbegin,ini-1] ini [ini+1,inend]
root->left = _buildTree(preorder,inorder,prei,inbegin,ini-1);
root->right = _buildTree(preorder,inorder,prei,ini+1,inend);
return root;
}
TreeNode* buildTree(vector& preorder, vector& inorder) {
int prei = 0;
int inbegin = 0,inend = inorder.size()-1;
return _buildTree(preorder,inorder,prei,inbegin,inend);
}
}; 
从中序与后序遍历序列构造二叉树
已知一颗二叉树中序为DBEHAFCG，后序为DHEBFGCA，构建出二叉树
第一步，后序序列最后一个字母为二叉树顶点，依题意得顶点为A。
第二步，在中序序列找到A的位置，排在A左边的所有字母（DBEH）组成左子树，排在E右边的所有字母（FCG）组成右子树。
第三步，看左子树部分（DBEH）在后序序列中的顺序，后序序列中左子树序列是（DHEB），由B排在最后一个可知，B就是左子树的根结点；
同理，看一下右子树部分（FCG），后序序列包含右子树部分的序列是（FGC），由C排在最后一个可知，C就是右子树的根结点。
已知一颗二叉树中序为DBEHAFCG，后序为DHEBFGCA，构建出二叉树
第四步，中序序列左子树部分（DEH），因为D在根结点A左边，所以D是A左子树，因为EH在根结点A右边，所以D是A右子树；
中序序列右子树部分（FG），因为F在根结点C左边，所以F组成C的左子树,因为G在根结点C右边，所以G组成C的左子树。
已知一颗二叉树中序为DBEHAFCG，后序为DHEBFGCA，构建出二叉树
第五步，看后序序列HE，E在后面所以E为B的右子树节点
第六步，看中序H在E的右边，所以H是E的右子树
后序是左子树，右子树，根
回到题目，后序倒着可以确定根，先构建根，然后构建右子树，再构建左子树，倒着构建即可构建出二叉树
class Solution {
public:
TreeNode* _buildTree(vector& inorder, vector& postorder,int& posi,int inbegin,int inend) {
if(inbegin > inend)
return nullptr;
TreeNode* root = new TreeNode(postorder[posi--]);//创建根；
int ini = inbegin;
while(ini <= inend)
{
if(inorder[ini] == root->val)
{
break;
}
else
ini++;
}
//分割出[inbegin,ini-1] ini [ini+1,inend]
root->right = _buildTree(inorder,postorder,posi,ini+1,inend);
root->left = _buildTree(inorder,postorder,posi,inbegin,ini-1);
return root;
}
TreeNode* buildTree(vector& inorder, vector& postorder) {
int posi = postorder.size()-1;
return _buildTree(inorder,postorder,posi,0,inorder.size()-1);
}
}; 二叉树前序非递归遍历
二叉树前序递归的过程是：根，左子树，右子树
非递归可以看作是先访问根，在访问左子树，再访问根，继续访问左子树..一直到nullptr，剩下没有被访问到的节点都是根节点的右子树
于是我们可以拆分成两个步骤
1.左路节点
2.左路节点的右子树
左路节点右子树划分成子问题不断循环解决
利用栈辅助，遇到左路节点入栈，先入8，3，1，出栈1，把1的右子树入栈、把3的右子树入栈、继续重复左路节点入栈操作
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector v;
stack s;
TreeNode* cur = root;
while(cur || !s.empty())
{
//访问左路节点
while(cur)
{
s.push(cur);
v.push_back(cur->val);
cur = cur->left;
}
TreeNode* top = s.top();//如果此节点从栈中取出，意味着其左节点和该节点已经访问完，还剩右节点
s.pop();
cur = top->right;//左路节点的右子树
}
return v;
}
}; 二叉树中序非递归遍历
中序和前序非递归的区别就是访问的时机不同，中序左子树，根，右子树
同样的把左路节点入栈，当走完左路节点后，开始出栈，出栈也就意味着左路节点已经结束，只剩右路节点，此时把出栈的节点push_back到vector中
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
stack st;
vector v;
TreeNode* cur = root;
while(cur || !st.empty())
{
// 开始访问一棵树
//1、左路节点
while(cur)
{
st.push(cur);
cur = cur->left;
}
//2.访问该节点和右子树
TreeNode* top = st.top();
st.pop();
v.push_back(top->val);
cur = top->right; // 子问题访问右子树
}
return v;
}
}; 二叉树后序非递归遍历
后序的区别就在于访问时机的不同
左路节点全部入栈，但是却不能随意出栈（只知道左树访问完，不知道右树是否存在）
分情况讨论：
1.出栈时，如果当前节点的右树为空，当前节点可以访问（左子树和右子树已经访问完）
2.出栈时，如果当前节点的右树不为空，当前节点不可以访问，转换为子问题，继续入左路节点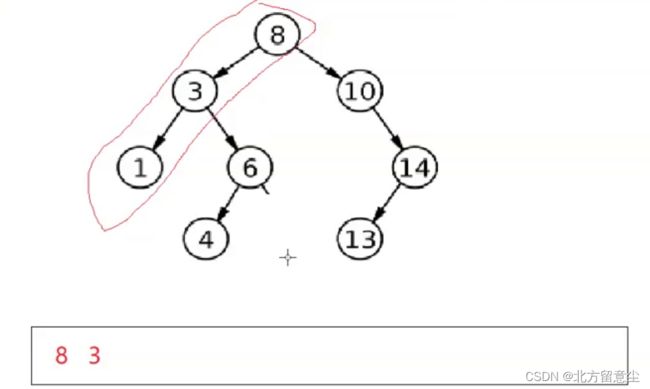
第一次走到3，3不能被访问，重复入栈左路节点，此时栈为8 3 6 4，当4左右为空时，可以取出4
出6，6的右树为空，出栈，当第二次走到3的时候，如果按照上面两种情况，无法区分当前节点是否可以被访问，就会死循环
解决方法：
我们设置prev，prev是上一次出栈的元素，第一次到3的时候，3的prev是1（后序的根节点都是最后被访问）；第二次到3的时候，prev的节点是6，当第二次到3的时候，3的prev == root->right，3可以出栈
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
vector v;
stack s;
TreeNode* cur = root;
TreeNode* prev = root;//记录当前节点的上一个位置
while(cur || !s.empty())
{
while(cur)
{
s.push(cur);
cur = cur->left;
}
TreeNode* top = s.top();
if(top->right == nullptr || top->right == prev)//如果prev==top->right，意味着第二次被访问
{
v.push_back(top->val);
prev = top;//prev记录节点
s.pop();
}
else//否则就是第一次被访问
{
cur = top->right;
}
}
return v;
}
};