prim算法

prim算法

prim算法(普利姆算法)：对图G(V,E)设置集合S，存放已访问的顶点，然后每次从集合V-S中选择与集合S的最短距离最小的一个顶点(记为u)，访问并加入集合S。之后，令顶点u为中介点，优化所有从u能到达的顶点v与集合S之间的最短距离。执行n次(n为顶点个数)，直到集合S已包含所有顶点。

算法实例演示

首先让我们来看一个example。如下图所示，图a是一个连通图（右图是图a对应的邻接矩阵，假设图中的边的权值大于0），我们现在基于该图来演示Prim算法的过程。


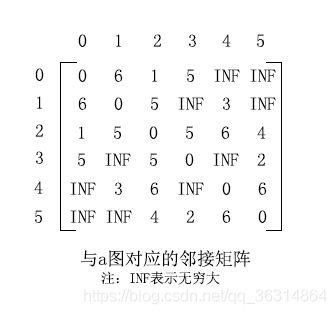
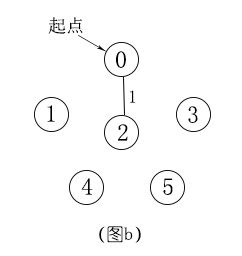
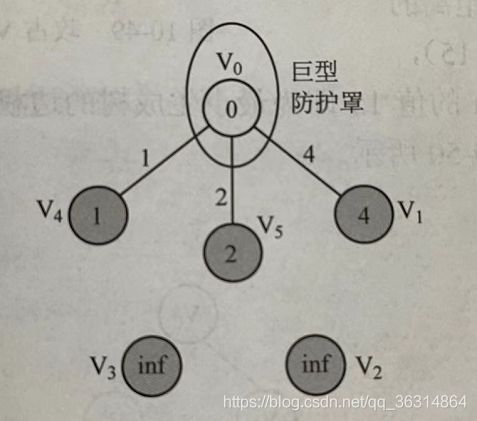
我们选择一个起点，然后在与起点相连且未被选的节点中选择一个权值最小的节点，将该节点与其相连边添加入生成树。假设起点是0节点，与0节点相连且未被选的节点是{1,2,3}，分别对应的权值是{6,1,5}，可见当前最小的权值1，权值最小的节点就是2节点，所以将2节点和0-2的边添加入生成树，如图b所示。

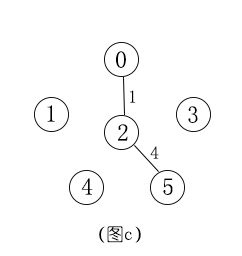
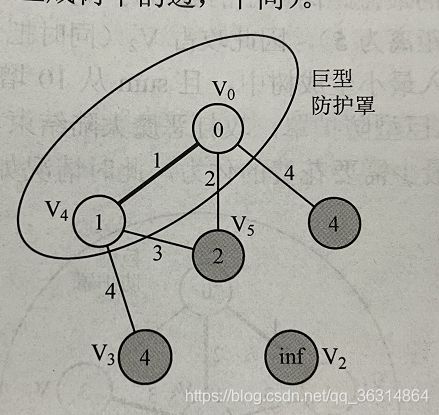
接着我们在与已选节点相连且未被选的节点中选择一个权值最小的节点，将该节点与其相连边添加入生成树。当前已选节点是0,2节点，与已选节点相连且未被选的节点有{1,3,4,5}，分别对应的权值是{（6,5），（5,5），6,4,}，可见当前最小的权值4，权值最小的节点就是5节点，所以将5节点和2-5的边添加入生成树，如图c所示。（其实在编程时，我们只需记录与更新当前较小的那个权值，如与{1,3,4,5}对应的权值我们只需记录{5,5,6,4}，当然我们也需利用了另一个数组来加以区别当前权值对应的连接点，如当前权值{5,5,6,4}所对应的连接点就是{2,0,2,2}）

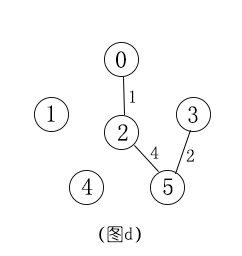
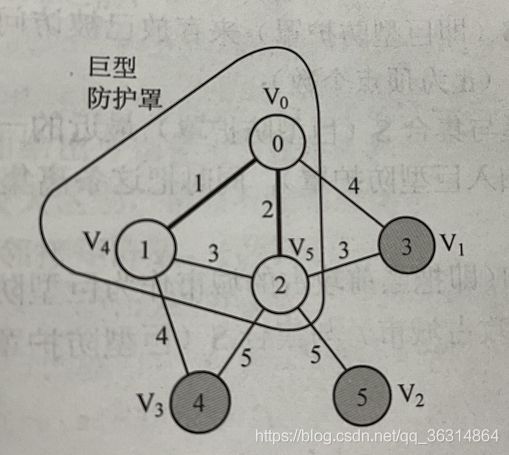
接着我们继续在与已选节点相连且未被选的节点中选择一个权值最小的节点，将该节点与其相连边添加入生成树。当前已选节点是0,2,5节点，与已选节点相连且未被选的节点有{1,3,4}，分别对应的权值是{（6,5），（2,5,5），（6,6）,}（其实当前我们可只记录{5,2,6}，同时记录其对应的连接点分别是{2,5,2}），可见当前最小的权值2，权值最小的节点就是3节点，所以将3节点和5-3的边添加入生成树，如图d所示。

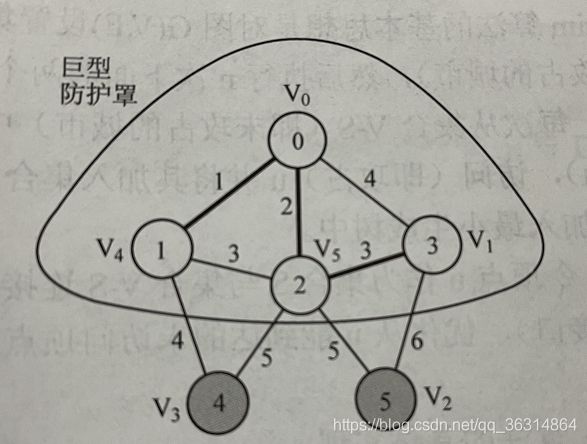
接着我们依照上一次的步骤继续在与已选节点相连且未被选的节点中选择一个权值最小的节点，将该节点与其相连边添加入生成树。如图e，f所示。最终图f就是我们通过Prim算法得到的最小生成树了。

prim算法基本思想：对图G(V,E)设置集合S来存放已被访问的顶点，然后执行n次下面的两个步骤(n为顶点个数)

1. 每次从集合V-S中选择与集合S最近的一个顶点(记为u)，访问u并将其加入集合S，同时把这条离集合S最近的边加入最小生成树。
2. 令顶点u作为集合S与集合V-S连接的接口，优化从u能到达的未访问顶点v与集合S的最短距离

prim算法的具体实现

1. 集合S的实现方法：使用一个bool型数组vis[]表示顶点是否已被访问。其中vis[i]==true表示顶点V_i已被访问，vis[i]==false则表示顶点V_i未被访问。
2. 不妨令int型数组d[]来存放顶点V_i(0<=i<=n-1)与集合S的最短距离。初始时除了起点s的d[s]赋为0，其余顶点都赋为一个很大的数来表示INF，即不可达。

prim算法与Dijkstra算法区别：
Dijkstra算法的数组d[]含义为起点s达到顶点V_i的最短距离。
prim算法的数组d[]含义为顶点V_i与集合S的最短距离

prim算法伪代码

Prim(G, d[])
{
	初始化;
	for(循环n次)
	{
		u = 使d[u]最小的还未被访问的顶点的标号;
		记u已被访问;
		for(从u出发能到达的所有顶点v)
		{
			if(v未被访问 && 以u为中介点使得v与集合S的最短距离d[v]更优)
			{
				将G[u][v]赋值给v与集合S的最短距离d[v];
			}
		}
	}
}

Dijkstra算法和prim算法实际上是相同思路，数组d[]含义不同。

定义MAXV为最大顶点数，INF为一个很大的数字

const int MAXV = 1000; //最大顶点数
const int INF = 100000000; //设INF为一个很大的数

1. 邻接矩阵版

int n, G[MAXV][MAXV]; //n为顶点数，MAXV为最大顶点数
int d[MAXV]; //顶点与集合S的最短距离
bool vis[MAXV] = {false}; //标记数组，vis[i] == true表示访问。初值均为false
intprim() //默认0号为初始点，函数返回最小生成树的边权之和
{
	fill(d, d + MAXV, INF); //fill函数将整个d数组赋为INF
	d[0] = 0; //只有0号顶点到集合S的距离为0，其余全是INF
	int ans = 0; //存放最小生成树的边权之和
	for(int i = 0; i < n; i++) //循环n次
	{
		int u = -1, MIN = INF; //u使d[u]最小，MIN存放该最小的d[u]
		for(int j = 0; j < n; j++) //找到未访问的顶点中d[]最小的
		{
			if(vis[j] == false && d[j] < MIN)
			{
				u = j;
				MIN = d[j];
			}
		}
		//找不到小于INF的d[u]，则剩下的顶点和集合S不连通
		if(u == -1)
			return -1;
		vis[u] = true; //标记u为已访问
		ans += d[u]; //将与集合S距离最小的边加入最小生成树
		for(int v = 0; v < n; v++)
		{
		    //v未访问 && u能到达v && 以u为中介点可以使v离集合S更近
			if(vis[v] == false && G[u][v] != INF && G[u][v] < d[v])
			{
				d[v] = G[u][v]; //将G[u][v]赋值给d[v]
			}
		}
	}
	return ans; //返回最小生成树的边权之和
}

2. 邻接表版

struct Node
{
	int v, dis; //v为边的目标顶点，dis为边权
};
vector<Node> Adj[MAXV]; //图G，Adj[u]存放从顶点u出发可以到达的所有顶点
int n; //n为顶点数，图G使用邻接表实现，MAXV为最大顶点数
int d[MAXV]; //顶点与集合S的最短距离
bool vis[MAXV] = {false}; //标记数组，vis[i] == true表示已访问。初值均为false

int prim() //默认0号为初始点，函数返回最小生成树的边权之和
{
	fill(d, d + MAXV, INF); //fill函数将整个d数组赋为INF
	d[0] = 0; //只有0号顶点到集合S的距离为0，其余全是INF
	int ans = 0; //存放最小生成树的边权之和
	for(int i = 0; i < n; i++) //循环n次
	{
		int u = -1, MIN = INF; //u使d[u]最小，MIN存放该最小的d[u]
		for(int j = 0; j < n; j++) //找到未访问的顶点中d[]最小的
		{
			if(vis[j] == false && d[j] < MIN)
			{
				u = j;
				MIN = d[j];
			}
		}
		//找不到小于INF的d[u]，则剩下的顶点和集合S不连通
		if(u == -1)
			return -1;
		vis[u] = true; //标记u为已访问
		ans += d[u]; //将与集合S距离最小的边加入最小生成树
		//只有下面这个for与邻接矩阵的写法不同
		for(int j = 0; j < Adj[u].size(); j++)
		{
			int v = Adj[u][j].v; //通过邻接表直接获得u能到达的顶点v
			if(vis[v] == false && Adj[u][j].dis < d[v])
			{
			    //如果v未访问 && 以u为中介点可以使v离集合S更近
				d[v] = Adj[u][j].dis;
			}
		}
	}
	return ans; //返回最小生成树的边权之和
}

例题

求最小生成树

从V₀开始，依次找到各顶点边权最小的，然后相连

#include 
#include 
using namespace std;
const int MAXV = 1000; //最大顶点数
const int INF = 1000000000; //设INF为一个很大的数

int n, m, G[MAXV][MAXV]; //n为顶点数，MAXV为最大顶点数
int d[MAXV]; //顶点与集合S的最短距离
bool vis[MAXV] = {false}; //标记数组，vis[i]==true表示已访问。初值均为false

int prim() //默认0号为初始点，函数返回最小生成树的边权之和
{
	fill(d, d + MAXV, INF); //fill函数将整个d数组赋为INF
	d[0] = 0; //只有0号顶点到集合S的距离为0，其余全是INF
	int ans = 0; //存放最小生成树的边权之和
	for(int i = 0; i < n; i++) //循环n次
	{
		int u = -1, MIN = INF; //u使d[u]最小，MIN存放该最小的d[u]
		for(int j = 0; j < n; j++) //找到未访问的顶点中d[]最小的
		{
			if(vis[j] == false && d[j] < MIN)
			{
				u = j;
				MIN = d[j];
			}
		}
		//找不到小于INF的d[u]，则剩下的顶点和集合S不连通
		if(u == -1)
			return -1;
		vis[u] = true; //标记u为已访问
		ans += d[u]; //将与集合S距离最小的边加入最小生成树
		for(int v = 0; v < n; v++)
		{
			//v未访问 && u能到达v && 以u为中介点可以使v离集合S更近
			if(vis[v] == false && G[u][v] != INF && G[u][v] < d[v])
			{
				d[v] = G[u][v]; //将G[u][v]赋值给d[v]
			}
		}
	}
	return ans; //返回最小生成树的边权之和
}

int main()
{
	int u, v, w;
	scanf("%d%d", &n, &m); //顶点个数、边数
	fill(G[0], G[0] + MAXV * MAXV, INF); //初始化图G
	for(int i = 0; i < m; i++)
	{
		scanf("%d%d%d", &u, &v, &w); //输入u,v以及边权
		G[u][v] = G[v][u] = w; //无向图
	}
	int ans = prim(); //prim算法入口
	printf("%d\n", ans);
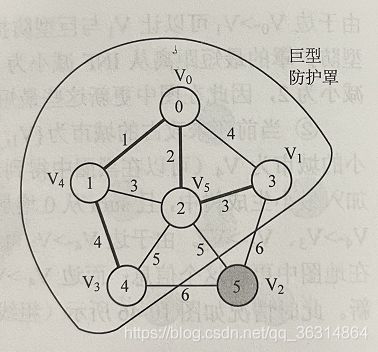
	return 0;
}

//输入数据
6 10 //6个顶点，10条边，以下10行10边
0 1 4 //边0->1与1->0的边权为4，下同
0 4 1
0 5 2
1 2 6
1 5 3
2 3 6
2 5 5
3 4 4
3 5 5
4 5 3

//输出结果
15