Java入门——进制(了解)
- 所有数字在计算机底层都以二进制的形式存在。
- 对于整数,有四种表示方式:
- 二进制(binary):0,1, 满2进1。以0b或0B开头。
- 十进制(decimal):0-9,满10进1.
- 八进制(octall):0-7,满8进1,以数字0开头表示。
- 十六进制(hex):0-9及A-F,满16进1。以0x或0X开头表示。此处的A-F 不区分大小写。如:0x21AF +1= 0X21B0
| 十进制 |
十六进制 |
八进制 |
二进制 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
10 |
| 3 |
3 |
3 |
11 |
| 4 |
4 |
4 |
100 |
| 5 |
5 |
5 |
101 |
| 6 |
6 |
6 |
110 |
| 7 |
7 |
7 |
111 |
| 8 |
8 |
10 |
1000 |
| 9 |
9 |
11 |
1001 |
| 10 |
A |
12 |
1010 |
| 11 |
B |
13 |
1011 |
| 12 |
C |
14 |
1100 |
| 13 |
D |
15 |
1101 |
| 14 |
E |
16 |
1110 |
| 15 |
F |
17 |
1111 |
| 16 |
10 |
20 |
10000 |
| 17 |
11 |
21 |
10001 |
计算机底层都以补码的方式来存储数据!
二进制数据的存储方式:所有的数值,不管正负,底层都以补码的方式存储。
原码、反码、补码的说明:
正数:三码合一
负数:
1.原码:直接将一个数值换成二进制数。最高位是符号位
2.负数的反码:是对原码按位取反,只是最高位(符号位)确定为1.
3.负数的补码:对其反码加1。
进制之间的基本转换
整数转换
1、十进制转二进制
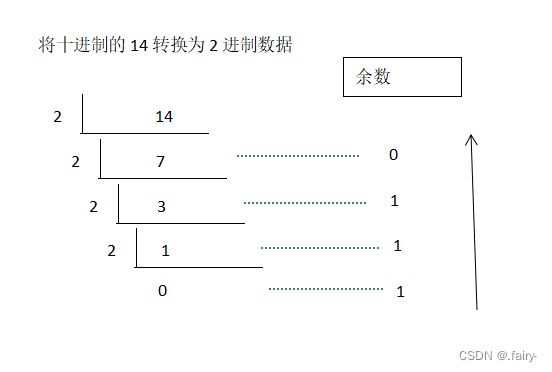
(1)十进制转二进制的转换原理:除以2,反向取余数,直到商为0终止。
(2)具体做法:
将某个十进制数除以2得到的整数部分保留,作为第二次除2时的被余数,得到的余数依次记下,重复上述步骤,知道整数部分为0就结束,将所有得到的余数最终逆序输出,则为该十进制对应的二进制数。
例如:14(十进制)---> 1110(二进制)
2、十进制转八进制
(1)转换原理:除以8,反向取余数,直到商为0终止。
(2)具体步骤与二进制一样
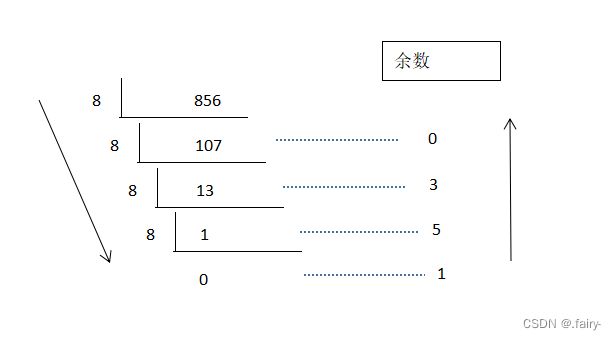
例如:十进制数856转换成八进制数:
将865除8取得第一个余数为0,将除8得到的整数部分107作为第二次的被除数,重复上述步骤 ,直到最终整数部分为0就结束。将取得的所有余数逆序输出。
则:865--->1530
3、十进制转十六进制
(1)转换原理:除以16,反向取余数,直到商为0终止
(2)具体步骤也和二进制、八进制一样,重复上述做法即可得到十六进制数。
例如:十进制数796转换为十六进制数
即为:796--->31c
需要注意的是,十六进制数是由0-9和A-F(或者(a-f)组成的,A相当于十进制中的10,B相当于11, 依次类推,F相当于15,上述示例中取得的余数12即为十六进制中的c。
总结:以上几种进制的整数部分转换原理都是除进制数取余数,倒叙输出。
小数部分进制表
| 指数 |
分数 |
二进制 |
十进制 |
| 2-1 |
1/2^1 |
.1 |
.5 |
| 2-2 |
1/2^2 |
.01 |
.25 |
| 2-3 |
1/2^3 |
.001 |
.125 |
| 2-4 |
1/2^4 |
.0001 |
.0625 |
| 2-5 |
1/2^5 |
.0000 1 |
.03125 |
| 2-6 |
1/2^6 |
.0000 01 |
.015625 |
小数部分转换
(1)原理:十进制小数转换成二进制小数采用“乘2取整,顺序输出”法。
例题:0.68D = ________B(精确到小数点后5位)
如下所示,0.68乘以2,取整,然后再将小数乘以2,取整,直到达到题目要求精度。得到结果:0.10101B。
例如:十进制小数0.68转换位二进制
具体步骤:
0.68*2=1.36----->1
0.36*2=0.72----->0
0.72* 2=1.44----->1
0.44* 2=0.88----->0
0.88* 2=1.76----->1已经达到了题目要求的精度,最后将取出整数部分顺序输出即可
则为:0.68D ---->0.10101B
(2)十进制转八进制
1)原理:十进制小数转换成八进制小数采用“乘8取整,顺序输出”法。
2)思路和十进制转二进制一样,参考如下例题:
例题:10.68D=________Q(精确到小数点后3位)
解析:整数部分除以8取余数,直到无法整除。小数部分0.68乘以8,取整,然后再将小数乘以8,取整,直到达到题目要求精度。得到结果:12.534Q
例如:十进制数10.68转换成八进制数,分为整数部分和小数部分求解
步骤:
(1)整数部分
10/8=1 -->2
1/8=0 -->1
倒序输出为12
(2)小数部分
0.68* 8=5.44 -->5
0.44* 8=3.52 -->3
0.52* 8=4.16 -->4
已经达到了题目要求的精度,即可结束
则小数部分为:0.68–>0.534
因此10.68D -->12.534Q
(3)十进制转十六进制
1)原理:十进制小数转换成十六进制小数采用“乘16取整,顺序输出”法。
2)思路也是一样的。
例题:25.67D=________H(精确到小数点后3位)
解析:如下图所示,整数部分除以16取余数,直到无法整除。小数部分0.68乘以16,取整,然后再将小数乘以16,取整,直到达到题目要求精度。得到结果:19.ae1H.
(1)整数部分
25/16=1 -->9
1/16=0 -->1
倒序输出为:19
(2)小数部分
0.68* 16=10.88 -->a(即十进制中的10)
0.88* 16=14.08 -->e
0.08* 16=1.28 -->1
已经达到了要求的精度,顺序输出为:ae1
则:25.68D -->19.ae1H
二进制、八进制、十六进制转换为十进制
整数转换
1、全部总结如下:
1011 [二进制] 0 1 当数位上的值超过1就要进1
1*2^3+0*2^2+1*2^1+1*2^0
=8+0+2+1
=11
1011 [八进制] 0 1 2 3 4 5 6 7 当前数位上的值超过7就要进1
1*8^3+0*8^2+1*8^1+1*8^0
=512+8+1
=521
1011 [十六进制] 0 1 2 3 4 5 6 7 8 9 A B C D E F 当前数位上的值超过15就要进1
1*16^3+0*16^2+1*16^1+1*16^0
=4096+16+1
=4113
2、三者转换原理都是一样的
例1:二进制与十进制的转换,带小数部分
01011010.01B
=0*2^7+1*2^6+0*2^5+1*2^4+1*2^3+0*2^2+1*2^1+0*2^0+0*2^(-1)+1*2^(-2)
= 90.25
例2:八进制与十进制的转换,如有小数部分,对应乘相应8的-i次方,【字母O,表示八进制】
345O
=3*8^2+4*8^1+5*8^0
=229
例3:十六进制与十进制的转换,如有小数部分,对应相乘16的-i次方【字母H,表示十六进制】
F2DH
=15*16^2+2*16^1+13*16^0
=3385
小数部分转换
1、二进制转十进制
(1)原理:整数部分按上述进行操作即可,小数部分从小数点后一位指数为-1开始算起,以后依次为-2、-3……
(2)具体运用以及步骤举例说明:
举例:将二进制0.1111转换成 十进制
| 二进制 |
0 |
. |
1 |
1 |
1 |
1 |
| 换算次方 |
2^(0) |
2^(-1) |
2^(-2) |
2^(-3) |
2^(-4) |
|
| 换成分数 |
0/2 |
1/2 |
1/4 |
1/8 |
1/16 |
|
| 换成十进制 |
0 + 0.5 + 0.25 + 0.125 + 0.0625 = 0.9375 |
|||||
2、八进制转十进制
(1)原理:整数部分操作以及运算不变,小数部分同二进制类似,将2改为8即可
(2)具体步骤方法如下:
例如:八进制数72.45转换成十进制数
步骤:
(1)整数部分:
7* 8^1+ 2* 8 ^0=58
(2)小数部分
4* 8^(-1) + 5* 8^(-2)=0.5+0.078125=0.578125
则为:72.45 -->58.578125
3、十六进制转十进制
(1)原理:整数运算一样,小数部分换成16即可
(2)具体方法步骤如下:
例:1A6.3B8=1* 16^2+A* 16 ^1+6* 16 ^0 +3* 16 ^(-1)+B* 16 ^(-2)+8* 16 ^(-3) =422.232422
总结:以上二进制、八进制、十六进制转换为十进制当中的整数部分从右往左指数从0开始递增,小数部分从左往右从-1开始递减,原理都是一样的。
例子说明:
二进制数1010 0100B转换成八进制数为244Q
二进制转换成八进制的方法是,取三合一法,即从二进制的小数点为分界点,向左(或向右)每三位取成一位。
二进制数1010 0100B转换成十六进制数为a4H
二进制转换成十六进制的方法是,取四合一法,即从二进制的小数点为分界点,向左(或向右)每四位取成一位。
八进制、十六进制转换成二进制
1、八进制数转换成二进制
原理:八进制数的一位是二进制数的三位
2、十六进制数转换成二进制数的四位
原理:十六进制数的一位是二进制数的四位
八进制与十六进制之间的转换
这两者之间的转换可以借助十进制或者二进制完成,可以先将八进制转换成十进制或二进制,再转换成十六进制。通过间接转换来实现。